这篇博客主要介绍了C++编程中的一些实用技巧，包括数字和字符串的转换、字符串操作、容器的使用以及算法的时间复杂度分析。还探讨了字母异位词判断、自定义排序函数、优先队列操作和处理链表、集合等数据结构的方法。此外，博主分享了处理大数、数组、字符串加法和乘法的策略，以及如何避免在类中初始化vector的常见错误。
自己在刷力扣的过程中，有时常在同一个问题上困惑，有时会碰到令自己眼前一亮的小技巧，于是专门写个博客收集记录一下，随时更新。
目录
找寻字符串中是否存在某个字符或子字符串、判断某个字符是否是给定的字符
在vecotr、list、priority_queue、map、set中构造键为pair的元素的操作
数字和字符串之间的转换
使用字符串流实现两者间的转换：
int num1 = 3983;
int num2;
string str1;
string str2 = "63856";
stringstream ss; //stringstream的头文件为#include<sstream>
ss << num1;
ss >> str1; //将数字转换为字符串
ss.clear(); //用完一次之后需要清空一下
ss << str2;
ss >> num2; //将字符串转换为数字
cout << str1 << endl;
cout << num2 << endl;使用to_string()函数实现从数字到字符串的转换：
int num1 = 3983;
string str1;
str1 = to_string(num1);
cout << str1 << endl;使用stoi(), stol(), stof(), stod()实现从字符串到数字的转换：
string str = "100";
int a = stoi(str);
float b = stof(str);
long long c = stol(str);
double d = stod(str);
cout << a << " " << b << " " << c << " " << d << endl;找寻字符串中是否存在某个字符或子字符串、判断某个字符是否是给定的字符
string vowel = "aeiou";
string str = "abcdefg"; //利用find()函数来寻找str中是否含有元音字母
for (int i = 0; i < str.size(); i++)
{
if (vowel.find(str[i]) != vowel.npos) //如果没有找到，find()函数将会返回npos
{
cout << str[i] << " ";
}
}
//输出：a e
string str = "abcdef";
string str2 = "cde";
cout << str.find(str2) << endl; //find()函数也能够用来寻找字符串
//输出2以某个字符为分界符，将字符串分割为多个单词
string str = " gh4jfsd 3dhf7ur k$df @sf ";
string temp;
stringstream ss;
ss << str;
string ans;
//以空格为分界符，将str分为多个单词，用斜线'/'隔开
while(getline(ss, temp, ' ')) //对于字符串流ss，以空格' '为分界符，将字符串放到temp中，一直读到ss为空
{
if (temp == "") //对于有连续多个空格的情况，避免输出多个斜线'/'
{
continue;
}
ans += temp + '/';
}
cout << ans;
//输出：gh4jfsd/3dhf7ur/k$df/@sf/截取字符串
string str1 = "welcome to my home";
//第一个参数是要截取的字符串的起始位置，后一个参数是要截取字符串的长度
//第一个参数从0开始计数；第二个参数从1开始计数，超过字符串长度的部分不计
string str2 = str1.substr(11, 7);
cout << str2;
//输出：my home
string str3 = str1.substr(11); //只有一个参数则默认截取到字符串结束
cout << str3;
//输出：my home字符串的插入和删除操作
string str = "welcome to my home";
str.insert(14, "beautiful "); //在第14个字符 'h' 之前插入字符串，即将新的字符串放在str的第14个字符之后
cout << str << endl;
//输出：welcome to my beautiful home
str.erase(14, 10); //从第14个字符 'b' 开始向后删除10个字符，超出的部分不计
cout << str << endl;
//输出：welcome to my home在vecotr、list、priority_queue、map、set中构造键为pair的元素的操作
//使用make_pair()函数可以不用指明类型，直接生成一个pair类型的对象
vector<pair<int, int>> vec;
vec.emplace_back(1, 3); //vector要使用emplace_back()函数
vec.emplace_back(make_pair(4, 5));
list<pair<int, int>> lis;
lis.emplace_back(1, 3); //list要使用emplace_back()函数
lis.emplace_back(make_pair(4, 5));
priority_queue<pair<int, int>> que;
que.emplace(1, 2); //priority_queue要使用emplace()函数
que.emplace(make_pair(4, 5));
//同理，队列queue也是使用emplace()函数
//unordered_map早已经不支持使用pair作为键，但是map还可以使用
//unordered_map也不支持使用vector作为键，但是map可以使用
map<pair<int, int>, int> maps;
pair<int, int> p(1, 3);
maps[make_pair(1, 3)]++;
maps[p]++;
cout << maps[p]; //输出2
set<pair<int, int>> sets;
sets.emplace(2, 3); //set要使用empalce()函数
sets.emplace(make_pair(6, 7));
//以下两种用法已经不再使用了，都会报错
unordered_map<pair<int, int>, int> maps;
unordered_set<pair<int, int>> sets;根据数据的规模拟定算法的时间复杂度
一秒内能出结果的数量级大概为10^7～10^8左右，看题目数据规模算一下，数据规模10^3的话O(n^2)就是10^6，完全是够的，如果数据规模10^5，必须考虑O(nlogn)
不过，根据做题的经验来说复杂度最好不要使数量级达到10^8，小于10^8最好。
字母异位词的判断
关于异位词，即由相同字母重排列形成的字符串（包括相同的字符串），如abbcd和bcadb。
这类词如果用哈希表判断太麻烦，用排序的话时间复杂度O(nlogn)又太大，最简单的还是用26个元素的数组int ch[26]来存储词频，判断两个字符串是否是异位词时只需要进行26次遍历即可。
在class中使用sort()的自定义比较函数
之前就吃过一次亏，在class中要使用sort()的自定义比较函数的话，必须声明为static，或者放在全局，如下：
//static bool compare(int x, int y) //或者将compare放在全局也行
//{
// return x > y;
//}
class Solution {
public:
static bool compare(int x, int y) //必须声明为static
{
return x > y; //降序
//return x < y; //升序
}
void findNthDigit() {
vector<int> vec = { 3,7,5,9,1 };
sort(vec.begin(), vec.end(), compare); //使用compare时不用加括号和参数
//sort(vec.begin(), vec.end(), greater<int>()); //注意，如果是直接使用greater来进行降序排列的话需要加括号
for (int i = 0; i < vec.size(); i++)
{
cout << vec[i] << " ";
}
}
};查找之后，找到了解释：
优先队列的自定义排序方法
这里采用的是自定义结构体和重载<运算符的方法
class Solution {
public:
struct Node
{
int i, j; //分别表示nums1中的下标和nums2中的下标
int x, y; //分别代表nums1[i]的值和nums2[j]的值
//因为优先队列默认使用<，所以要重载<
//这里的两个const都必须添加
bool operator< (const Node& a) const
//这里的<比较的是优先级，而不是比较大小，返回true时，说明this的优先级低于a
//x + y值较大的Node优先级低（x + y小的Node排在队前）
{
return x + y > a.x + a.y;
}
};
vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {
priority_queue<Node> prique;
}
};这里的两个const不能省略，第一个const修饰的是a，第二个const修饰的是this，因为在原优先队列的比较函数中就是使用两个常数来比较：
// STRUCT TEMPLATE less
template <class _Ty = void>
struct less {
_CXX17_DEPRECATE_ADAPTOR_TYPEDEFS typedef _Ty _FIRST_ARGUMENT_TYPE_NAME;
_CXX17_DEPRECATE_ADAPTOR_TYPEDEFS typedef _Ty _SECOND_ARGUMENT_TYPE_NAME;
_CXX17_DEPRECATE_ADAPTOR_TYPEDEFS typedef bool _RESULT_TYPE_NAME;
_NODISCARD constexpr bool operator()(const _Ty& _Left, const _Ty& _Right) const {
return _Left < _Right;
}
};这个是优先队列的源码，原本就是用两个const修饰的变量_Left 和 _Right来比较的，重载<运算符后，_Left < _Right就相当于_Left .operator<( _Right )，所以重载<运算符的时候第一个const是为了能够接受_Right，第二个const是让_left可以调用函数（实际上第二个const就是修饰this的）。
所以去掉两个const的话，就相当于要将两个常数传入可以修改他们值的函数中，这是不允许的。
在类中不能直接初始化vector
以下代码中，vector<int> b(3)是错误的：
class test
{
vector<int> a; //正确
vector<int> b(3, 0); //错误，出现提示应输入类型说明符
};若改成以下形式，则是正确的：
class test
{
vector<int> a; //正确
vector<int> b; //错误，出现提示应输入类型说明符
test()
{
b.resize(3, 0);
}
};究其原因，就是因为在类中的成员变量，只有静态整型才能够初始化，其他的成员变量只能够在构造函数或者其他的成员函数中初始化。
将无重复字母的单词转换为二进制数存储
set<int> sets;
//startWords中的各个单词，都由无重复的字母组成，即最长长度为26
for (string str : startWords)
{
int x = 0;
for (char ch : str)
{
x ^= 1 << (ch - 'a'); //利用异或运算，将各个单词转换为对应的二进制数
}
sets.insert(x);
}字符串的加法和乘法
直接利用字符串进行运算的一大好处就是，可以避免数字因过长而溢出，例如这道题目：力扣
加法：
class Solution {
public:
string addStrings(string num1, string num2) {
int i = num1.size() - 1; //指针1
int j = num2.size() - 1; //指针2
int carry = 0; //进位标志
string ans;
//carry的作用：当num1和num2都已经遍历完，但是还有进位即carry为1时，继续进入循环
while (i >= 0 || j >= 0 || carry)
{
int cur1 = i >= 0 ? num1[i] - '0' : 0;
int cur2 = j >= 0 ? num2[j] - '0' : 0;
int temp = cur1 + cur2 + carry;
carry = temp / 10;
char ch = temp % 10 + '0';
ans = ch + ans;
i--;
j--;
}
return ans;
}
};关于遍历并访问容器中的元素的问题
map<vector<int>, int> maps;
vector<int> a = { 99,100 };
maps[a]++;
//使用以下这种方法遍历哈希表时，需要用->来访问哈希表中的键或者值
for (auto iter = maps.begin(); iter != maps.end(); iter++)
{
cout << iter->first[0] << endl; //输出99
cout << iter->second << endl; //输出1
}
//使用以下这种方法遍历哈希表时，需要使用.来访问哈希表中的键或值
for (auto iter : maps)
{
cout << iter.first[0] << endl; //输出99
cout << iter.second; //输出1
} //使用.访问pair中的元素
pair<int, int> p(2, 3);
cout << p.first << endl; //输出2
cout << p.second << endl; //输出3 list<int> lis;
lis.push_back(10);
//使用以下这种方法遍历链表时，需要使用*来访问链表中的元素
for (auto iter = lis.begin(); iter != lis.end(); iter++)
{
cout << *iter << endl; //输出10
}
//使用以下这种方法遍历链表时，可以直接访问链表中的元素
for (auto iter : lis)
{
cout << iter << endl; //输出10
}
set<int> s;
s.insert(10);
//使用以下方式遍历set时，需要加*来访问元素
for (auto iter = s.begin(); iter != s.end(); iter++)
{
cout << *iter << endl; //输出10
}
//使用以下方式遍历set时，可以直接访问元素
for (auto iter : s)
{
cout << iter << endl; //输出10
}访问vector中的pair：
vector<pair<int, char>> prique = {{3, 'a'}, {4, 'b'}, {5, 'c'}};
string ans;
for (auto& [cnt, ch] : prique)
{
cout << cht << " " << ch << endl;
cnt--; //这里的操作能够直接作用于vector中元素的值
}前后缀元素个数、前后缀和、前后缀最大值
每次有关前缀后缀的题目，思路倒是容易想到，但是我总会出现下标越界等问题，特此总结一下。
计算前缀后缀元素个数：
vector<int> nums = { 1, 0, 1, 0, 1, 0 };
int n = nums.size();
vector<int> pre(n + 1, 0), rea(n + 1, 0);
//前缀0的个数（不包括自身）
pre[0] = 0; //不包括自身的情况下，计算pre[0]不能放在遍历中，否则遍历时在数组nums和pre中都会越界
//这里要注意，题目要求的下标i最大是否能够等于n
for (int i = 1; i <= n; i++)
{
pre[i] = nums[i - 1] == 0 ? pre[i - 1] + 1 : pre[i - 1];
}
for (int i = 0; i <= n; i++)
{
cout << pre[i] << " "; //输出0 0 1 1 2 2 3
}cout << endl;
//前缀0的个数（包括自身）
pre[0] = nums[0] == 0 ? 1 : 0; //包括自身的情况下，计算pre[0]不能放在遍历中，否则遍历时在数组pre中会越界
//包括自身的情况下，下标i最大肯定是不能够等于n的，否则在数组nums中会越界
for (int i = 1; i < n; i++)
{
pre[i] = nums[i] == 0 ? pre[i - 1] + 1 : pre[i - 1];
}
for (int i = 0; i < n; i++)
{
cout << pre[i] << " "; //输出0 1 1 2 2 3
}cout << endl;
//后缀1的个数（不包括自身）
rea[n - 1] = 0; //不包括自身的情况下，计算rea[n - 1]不能放在遍历中，否则遍历时在数组nums和rea中都会越界
//这里要注意，由于下标最小只能到0，所以在不包括自身的情况下nums[0]是否为1无法被考虑到，除非题目的下标是1 - n
for (int i = n - 2; i >= 0; i--)
{
rea[i] = nums[i + 1] == 1 ? rea[i + 1] + 1 : rea[i + 1];
}
for (int i = 0; i < n; i++)
{
cout << rea[i] << " "; //输出2 2 1 1 0 0
}cout << endl;
//后缀1的个数（包括自身）
rea[n - 1] = nums[n - 1] == 1 ? 1 : 0; //包括自身的情况下，计算rea[n - 1]不能放在遍历中，否则遍历时在rea中会越界
//包括自身的情况下，nums[0]当然会被考虑到
for (int i = n - 2; i >= 0; i--)
{
rea[i] = nums[i] == 1 ? rea[i + 1] + 1 : rea[i + 1];
}
for (int i = 0; i < n; i++)
{
cout << rea[i] << " "; //输出3 2 2 1 1 0
}cout << endl;计算前缀后缀和：
vector<int> nums = { 1, 2, 3, 4, 5, 6 };
int n = nums.size();
vector<int> pre(n + 1, 0), rea(n + 1, 0);
//前缀和（不包括自身）
pre[0] = 0; //不包括自身的情况下，计算pre[0]不能放在遍历中，否则遍历时在数组nums和pre中都会越界
//这里要注意，题目要求的下标i最大是否能够等于n
for (int i = 1; i <= n; i++)
{
pre[i] = pre[i - 1] + nums[i - 1];
}
for (int i = 0; i <= n; i++)
{
cout << pre[i] << " "; //输出0 1 3 6 10 15 21
}cout << endl;
//前缀和（包括自身）
pre[0] = nums[0]; //包括自身的情况下，计算pre[0]不能放在遍历中，否则遍历时在数组pre中会越界
//包括自身的情况下，下标i最大肯定是不能够等于n的，否则在数组nums中会越界
for (int i = 1; i < n; i++)
{
pre[i] = pre[i - 1] + nums[i];
}
for (int i = 0; i < n; i++)
{
cout << pre[i] << " "; //输出1 3 6 10 15 21
}cout << endl;
//后缀和（不包括自身）
rea[n - 1] = 0; //不包括自身的情况下，计算rea[n - 1]不能放在遍历中，否则遍历时在数组nums和rea中都会越界
//这里要注意，由于下标最小只能到0，所以在不包括自身的情况下nums[0]无法被计算进来，除非题目的下标是1 - n
for (int i = n - 2; i >= 0; i--)
{
rea[i] = rea[i + 1] + nums[i + 1];
}
for (int i = 0; i < n; i++)
{
cout << rea[i] << " "; //输出20 18 115 11 6 0
}cout << endl;
//后缀和（包括自身）
rea[n - 1] = nums[n - 1]; //包括自身的情况下，计算rea[n - 1]不能放在遍历中，否则遍历时在rea中会越界
//包括自身的情况下，nums[0]当然会被计算进来
for (int i = n - 2; i >= 0; i--)
{
rea[i] = rea[i + 1] + nums[i];
}
for (int i = 0; i < n; i++)
{
cout << rea[i] << " "; //输出21 20 18 15 11 6
}cout << endl;计算前缀后缀最大值：
vector<int> nums = { 3, 2, 5, 6, 1, 4 };
int n = nums.size();
vector<int> pre(n + 1, 0), rea(n + 1, 0);
//前缀最大值（不包括自身）
pre[0] = 0; //不包括自身的情况下，计算pre[0]不能放在遍历中，否则遍历时在数组nums和pre中都会越界
//这里要注意，题目要求的下标i最大是否能够等于n
for (int i = 1; i <= n; i++)
{
pre[i] = max(pre[i - 1], nums[i - 1]);
}
for (int i = 0; i <= n; i++)
{
cout << pre[i] << " "; //输出0 3 3 5 6 6 6
}cout << endl;
//前缀最大值（包括自身）
pre[0] = nums[0]; //包括自身的情况下，计算pre[0]不能放在遍历中，否则遍历时在数组pre中会越界
//包括自身的情况下，下标i最大肯定是不能够等于n的，否则在数组nums中会越界
for (int i = 1; i < n; i++)
{
pre[i] = max(pre[i - 1], nums[i]);
}
for (int i = 0; i < n; i++)
{
cout << pre[i] << " "; //输出3 3 5 6 6 6
}cout << endl;
//后缀最大值（不包括自身）
rea[n - 1] = 0; //不包括自身的情况下，计算rea[n - 1]不能放在遍历中，否则遍历时在数组nums和rea中都会越界
//这里要注意，由于下标最小只能到0，所以在不包括自身的情况下nums[0]无法被考虑到，除非题目的下标是1 - n
for (int i = n - 2; i >= 0; i--)
{
rea[i] = max(rea[i + 1],nums[i + 1]);
}
for (int i = 0; i < n; i++)
{
cout << rea[i] << " "; //输出6 6 6 4 4 0
}cout << endl;
//后缀最大值（包括自身）
rea[n - 1] = nums[n - 1]; //包括自身的情况下，计算rea[n - 1]不能放在遍历中，否则遍历时在rea中会越界
//包括自身的情况下，nums[0]当然会被考虑到
for (int i = n - 2; i >= 0; i--)
{
rea[i] = max(rea[i + 1], nums[i]);
}
for (int i = 0; i < n; i++)
{
cout << rea[i] << " "; //输出6 6 6 6 4 4
}cout << endl;可以看到前后缀元素个数、和、最大值三种形式，其实都是同一个模板，就是计算公式不同罢了，总结一下，有几点需要注意的：
· 无论是否“包括自身”，首元素/尾元素对应的值最好都放在遍历前额外设置，防止越界
· 在“不包括自身”的情况下，前缀和后缀都要特别关注最后一个下标是否可以被考虑到（第一个下标没有特别要求）
· 如果nums的元素个数为n，在“不包括自身”的情况下，前缀后缀的数组要设置的比n大一点，使得能够考虑到最后一个元素
· 在“不包括自身”的情况下，就是 pre[i - 1] 和 nums[i - 1] 、rea[i + 1] 和 nums[i + 1] 参与计算
“包括自身”的情况下，就是 pre[i - 1] 和 nums[i] 、rea[i + 1] 和 nums[i] 参与计算
一些运算公式
模运算解决数据溢出问题
当遇到一些数值较大的题目时，往往需要在计算过程中随时取模，这就涉及到了两个常用的模运算公式：
1、(a * b) % m = ((a % m) * (b % m)) % m
2、(a + b) % m = ((a % m) + (b % m)) % m
位运算实现加减法
当 mid 是偶数/奇数时，与位运算的转换：
1、当mid是偶数时，mid + 1 = mid ^ 1
2、当mid是奇数时，mid - 1 = mid ^ 1
n&(n-1)
此法还可以用来判断n是否为2的幂：如果n大于0，并且n&(n-1)等于0，那么说明n为2的幂
位运算实现加法操作
例题：剑指 Offer 65. 不用加减乘除做加法 - 力扣（LeetCode）
分析过程：
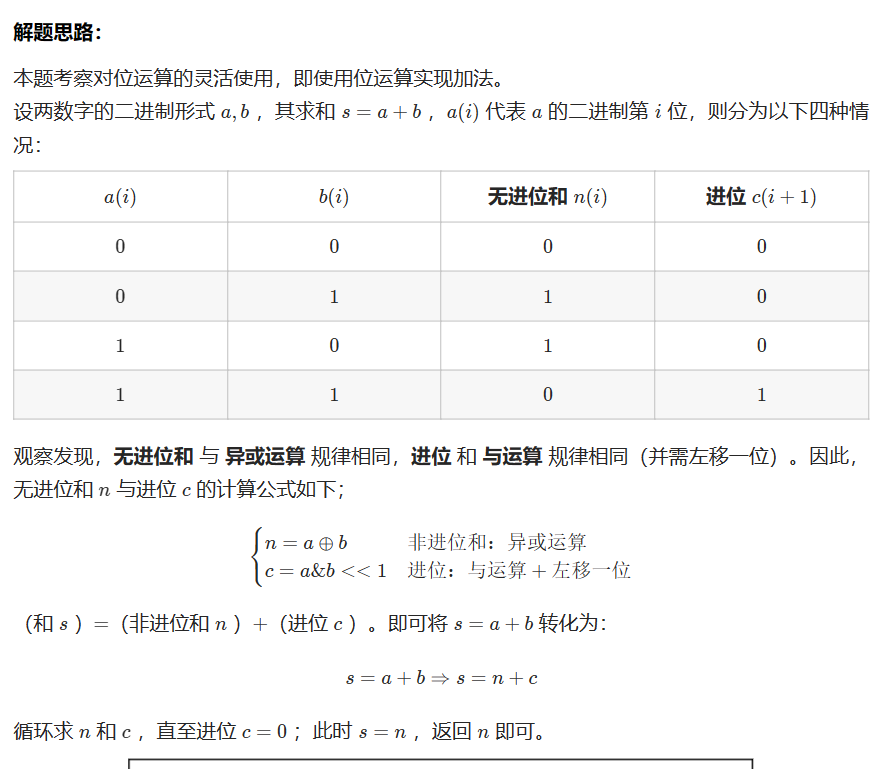
有点编译器可能不支持C++的负数左移，例如leetcode就不行，因此在左移操作前要加上(unsigned int)，先将数字转换为无符号类型
最小公因数与最大公倍数的关系
例题：2470. 最小公倍数为 K 的子数组数目 - 力扣（LeetCode）
两个自然数的乘积等于这两个数的最大公因数和最小公倍数的乘积
例如：6 × 8 = 2 × 24
求非常巨大的数字的因数
如果要求一些十分巨大的数字的因数，例如2021041820210418，这个数字共有16位，如果直接用暴力求：
long long n = 2021041820210418;
long long ans = 0;
vector<long long> vec;
for (long long i = 1; i <= n; i++)
{
if (n % i == 0)
{
vec.push_back(i);
}
}那么将会十分困难，甚至需要好几天才能算出来。
但如果对n取根号，那就可以将复杂度简化到10 ^ 8，并且每遇见一个因数i，就可以用n / i直接求出与其相对应的另一个较大的因数。如下：
long long n = 2021041820210418;
long long ans = 0;
vector<long long> vec;
for (long long i = 1; i <= sqrt(n); i++)
{
if (n % i == 0)
{
vec.push_back(i);
//例如如果n为4的话，如果不加判断将会加入两个2
if (i != n / 2)
vec.push_back(n / i);
}
}关于在函数中初始化指针的问题
感谢这位兄弟的解释：(9条消息) c语言,关于初始化函数间链表地址传递问题浅析_龍龍哥的博客-优快云博客
起因是之前写递归函数时，我想直接在函数中初始化后续节点，如下所示：
struct node
{
int val;
node* next;
};
void func(node* cur)
{
cur = new node;
cur->val = 3;
}
int main() {
node* root = new node;
func(root->next); //原意是想在函数中初始化root->next
cout << root->next->val << endl; //崩溃，无法输出
return 0;
}上述文章中的解释是这样的：
虽然我的代码在进入函数前没有先初始化root->next，但是因为是在函数中初始化了root->next，所以当函数结束时在函数中初始化的数据并不会返回。
因此有两种解决办法，一种是先初始化节点，再传入函数中：
struct node
{
int val;
node* next;
};
void func(node* cur)
{
cur->val = 3;
}
int main() {
node* root = new node;
root->next = new node; //先将root->next在函数外初始化
func(root->next);
cout << root->next->val << endl; //输出3
return 0;
}另一种是将在函数中初始化完的结点返回：
struct node
{
int val;
node* next;
};
node* func(node* cur)
{
cur = new node;
cur->val = 3;
return cur; //将初始化后的结点返回
}
int main() {
node* root = new node;
root->next = func(root->next);
cout << root->next->val << endl; //输出3
return 0;
}使用new初始化数组的方法
一维：
int n = 2;
int* a = new int[n];二维：
int m = 3, n = 2;
int** a = new int* [m];
for (int i = 0; i < m; i++)
{
a[i] = new int[n];
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
