PCA改进算法——2DPCA算法（web信息检索实验）

PCA改进算法——2DPCA算法

摘要：在学习降维算法的过程中，我们主要学习了四种降维算法，包括PCA（Principal Components Analysis）、LDA（Linear Discriminant Analysis）、LLE（Locality linear embedding）、LE（Laplacian Eigenmaps）。其中，PCA——主成分分析算法是非常常用的一种线性降维算法，其实现较为简单，也就意味着它在使用中能有较大的改进空间，在这篇报告中，将要说明的就是一种PCA的改进算法——2DPCA。

1. PCA简介

1.1简介

PCA，全名主成分分析方法。其目标是通过某种线性投影，将高维的数据映射到低维的空间中表示，并期望在所投影的维度上数据的方差最大，以此使用较少的数据维度，同是保留住较多的原数据点的特性。

从数学角度可以解释，如果把所有的点都映射到一起，那么几乎所有的信息都会丢失，如果方差能够尽可能的大，代表着数据点之间的距离越大，数据点因此会分散开，这样能够保留更多的信息。

PCA作为一个最经典的特征提取和数据压缩的技术，被广泛的应用于计算机的各个领域。

2. 2DPCA分析

2.1 简介

PCA的方法是将多维的矩阵转化成一维向量。由于其维数过大，通过这种方式转化出来的1维向量可能胡导致难以计算多维矩阵的协方差。虽然现在可以通过SVD的方法，较为简单的处理这些数据，得到准确的协方差，但其仍然有缺陷——通过这种方法，难以得到较为准确的特征向量。

介于以上的因素，two-dimentional principal component analysis（2DPCA）被考虑出来用于解决问题。相对于PCA基于1维的向量处理，2DPCA所不同的是其基于2维的矩阵来处理问题。所以这种方法能够更准确的计算协方差，决定最适合的特征向量所需的时间也更少。

2.2算法

设X表示n维列向量，将m*n的图像矩阵A通过如下的线性变化直接投影到X上：

Y = AX

Y是我们得到的一个投影的m维的向量，又被称作图像矩阵A的投影的特征向量。最佳投影方向X有特征向量Y的散度分布情况来决定，采用：

J(x) = tr(Sx)

其中Sx代表训练样本的投影特征向量的协方差矩阵，tr(Sx)代表Sx的迹，可以通过它来反应投影后样本间的散度。具体计算方式如下

Sx = E(Y-EY)(Y-EY)T = E[AX- E(AX)] [AX - E(AX)]T 

= E[(A - EA)X][(A – EA)X]T 

tr(Sx) = Xt[E(A – EA)T(A - EA)]

tr(Sx)的中间部分恰好是图像矩阵A的协方差矩阵，所以单独定义为Gt：

Gt= E(A – EA)T(A - EA)

Gt是一个n*n的非负定矩阵。假设有M个训练样本，Aj(j=1,2,…,M)，Gt可以通过以下公式计算：

 

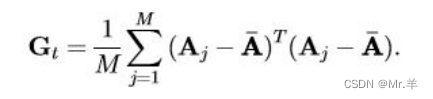
根据上述条件，可以将J(X)用以下等式表示：

J(X)=XTGtX‘

其中，X是单位列向量，这个标准也被称为广义总散射标准，最大化标准的独立向量X为最佳投影轴。

最佳投影轴Xopt是最大化J(X)的单位向量，即Gt的特征向量对应于最大特征值。而一般来说，只有一个最佳投影轴是不够的。所以就需要选择一组投影轴X1,…,Xd，即：

而最佳投影轴X1,…,Xd是Gt的正交特征向量，对应前d个最大特征值。

3. 总结

2DPCA对比原始PCA的优点有着很明显的一点就是无需将图像向量化，能够大幅减少计算特征向量的时间，同时，直接基于图像矩阵使得图像特征提取更加简单也更直接；另一方面，需要做特征值分解的协方差矩阵相比较而言，尺寸更小一点，计算带来的开销也会相应的减少。

如果应用在图像识别中的例子来说，同样100张的100*100的图片，原始PCA所需的协方差矩阵尺寸为100*10000，而如果应用2DPCA，则仅仅需要仍为100*100的协方差矩阵。

但在提高了一些性能的同时，在其他方面也是会付出一定代价的，由于PCA需要较少的图像表示系数，PCA在存储需求方面会更高效一些。

2DPCA的提出者还在文末表示了这种方法还有许多值得深入研究的地方。说明这种方法仍有可以改进的地方。

4. 参考文献

Jian Yang; D. Zhang; A. F. Frangi; Jing-yu Yang ,“Two-dimensional PCA: a new approach to appearance-based face representation and recognition“，14 June 2004