leetcode 二分法总结

按照35，34的顺序刷题能更好的理解二分法！！！！

35 搜索插入位置

 给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1

 注意：

• nums 为 无重复元素 的 升序 排列数组

1.题目规定不会存在重复数字，所以如果数组中存在目标数字，返回值就是mid的值，因为二分法执行完后，mid指向的一定是目标数字位置（目标数字存在且无重复的情况）。

2.如果数组中不存在，为了方便理解，我们假设先按序插入目标数字，这样我们只需要找到排序后target的位置记左边界。（实际上是定位到第一个大于或等于target的数的位置 ）

实际上，对于边界我们往往分开区间和闭区间（如下图，target = 8时，实际上我们要boundary -> nums[i] = 9，这是闭区间，即左边界就是boundary指向的位置，如果是开区间那么
boundary -> nums[i] = 7，但最后插入的话要 + 1），实际上这也和判断条件有关，同样的执行代码，如果是while(left <= right )，那么mid最后一定指向nums[i] = 9的位置，但如果是while(left < right)，那么最后只能指向7。

                                        ​​​​​​​        

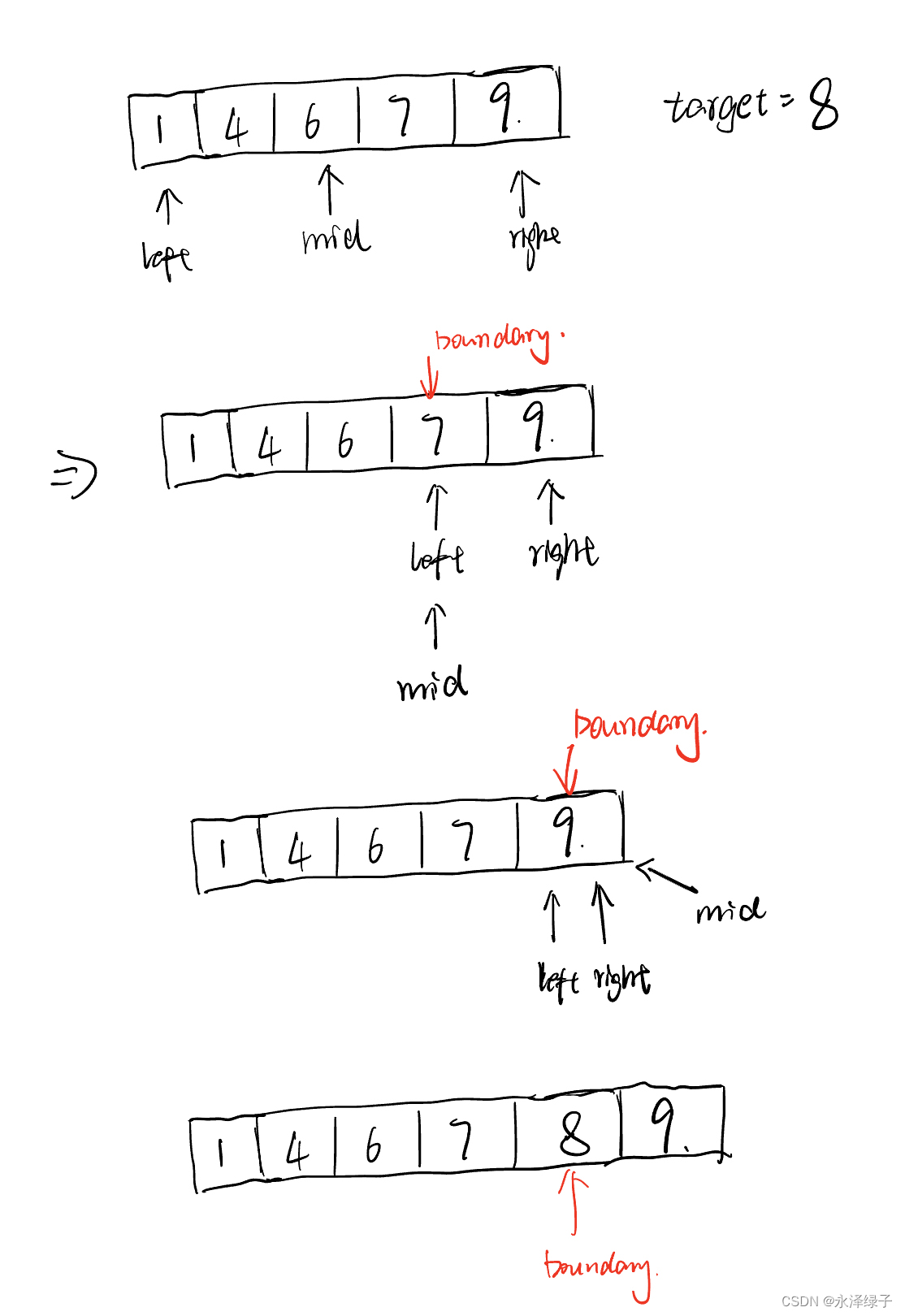
这里我们选闭区间，下面是官方给出找左边界的代码：

class Solution {
    public int searchInsert(int[] nums, int target) {
        int n = nums.length;
        int left = 0, right = n - 1, ans = n;
        while (left <= right) {
            int mid = ((right - left) >> 1) + left;
            if (target <= nums[mid]) {
                ans = mid;
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return ans;
    }
}

可以看到这与普通版本的区别是，找到目标数后并未直接返回，而是双指针遍历完所有的数后的下一轮返回ans的值，即上文boundary。

接下来看升级版本，更进一步的应用！！！！ 

34 在排序数组中查找元素的第一个和最后一个位置

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

注意：这里与上一题不同的地方是数组中允许有重复的数字！！同时我们需要找到闭区间的左右边界。
 

下面是官方解答：

class Solution { 
public:
    int binarySearch(vector<int>& nums, int target, bool lower) {
        int left = 0, right = (int)nums.size() - 1, ans = (int)nums.size();
        while (left <= right) {
            int mid = (left + right) / 2;
            if (nums[mid] > target || (lower && nums[mid] >= target)) {
                right = mid - 1;
                ans = mid;
            } else {
                left = mid + 1;
            }
        }
        return ans;
    }

    vector<int> searchRange(vector<int>& nums, int target) {
        int leftIdx = binarySearch(nums, target, true);
        int rightIdx = binarySearch(nums, target, false) - 1;
        if (leftIdx <= rightIdx && rightIdx < nums.size() && nums[leftIdx] == target && nums[rightIdx] == target) {
            return vector<int>{leftIdx, rightIdx};
        } 
        return vector<int>{-1, -1};
    }
};

我们先来看左边界的情况，即lower == true。此时变成了

class Solution { 
public:
    int binarySearch(vector<int>& nums, int target, bool lower) {
        int left = 0, right = (int)nums.size() - 1, ans = (int)nums.size();
        while (left <= right) {
            int mid = (left + right) / 2;
            if (nums[mid] >= target) {
                right = mid - 1;
                ans = mid;
            } else {
                left = mid + 1;
            }
        }
        return ans;
    }

我们发现和上一道题目的代码一样，但是这里有不一样的解释，

因为左边界需要不断往左边靠拢，所以当target == nums[mid]的时候，有可能出现下图中第二行的情况，target = 7，但是不止一个7，有可能找到的是中间的7，此时我们需要将边界指针boundary继续向左移动。

                                  ​​​​​​​        ​​​​​​​        

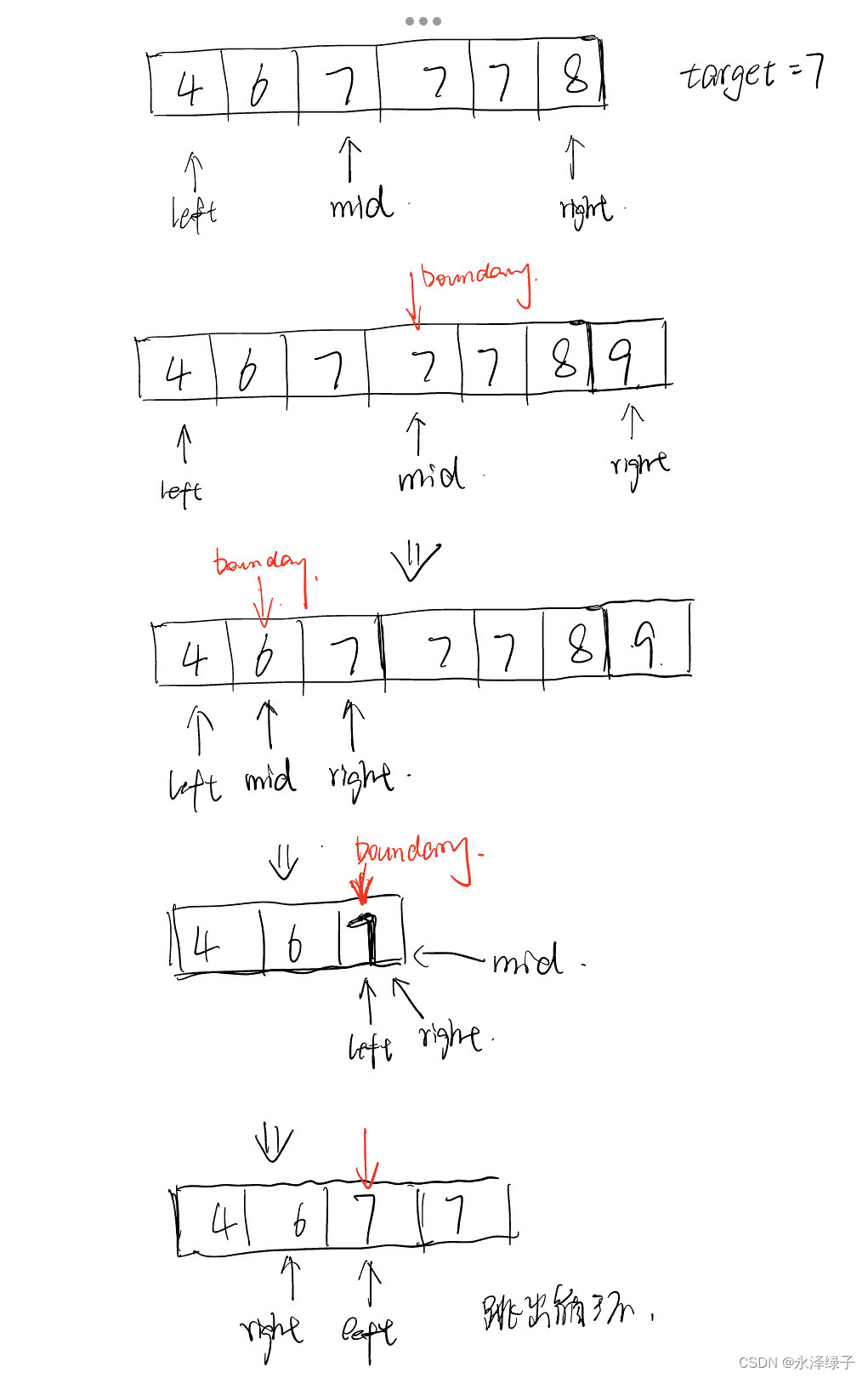
所以，这里当nums[mid] == target的时候，因为我们需要将right指针向左移动，让算法来寻找mid左边的重复目标数，同时记录mid的值。（注意，一定要在nums[mid] == target时记录boundary）找右边界也是同样的道理。

总结：二分法可以用来找边界，也可以用来找目标数的位置