凸优化 matlab-cvx-第十一章ADVANCED TOPICS

注意：在本节中，我们描述了CVX的一些更高级的功能。我们建议你先跳过这一节，直到你对上面描述的基本能力感到满意为止。

11.1消除二次型

我们强烈建议的一个特殊的改写是消除二次型- -即像sum _ square，sum ( square ( . ) )或quad_ form这样的函数- -只要有可能使用范数来构造等价模型。我们的经验告诉我们，二次型对于CVX所使用的底层求解器来说常常是一个数值挑战。

我们承认，这种建议违背了传统的智慧：二次型是典型的光滑凸函数，而范数是非光滑的，因此是笨拙的。但是对于CVX使用的圆锥曲线求解器，这种智慧恰恰是倒退的。它是最适合于圆锥体配方和解决方案的规范。实际上，二次形式是通过将它们转换为圆锥形形式使用规范来处理的!这个转换过程提出了一些有趣的缩放挑战。如果建模者能够消除执行这种转换的需要，那就更好了。

对于这种变化的一个简单例子，考虑目标

minimize( sum_square( A * x - b ) )

在精确算术中，这恰好等价于

minimize( square_pos( norm( A * x - b ) ) )

但是如果我们完全消去平方，等价性也被保留了：

minimize( norm( A * x - b ) )

x的最优值在所有三种情况下都是相同的，但最后一个版本可能会产生更准确的结果。当然，如果你需要平方范数的值，你可以通过在事实之后平方范数来恢复它。

使用Quadrature _ Form的转换有时会比较困难。例如，考虑

 quad_form( A * x - b, Q ) <= 1

其中Q是一个正定矩阵。等效规范版本是

norm( Qsqrt * ( A * x - b ) ) <= 1

其中，Qsqrt是Q的一个合适的矩阵平方根。一种选择是计算对称平方根Qsqrt = sqrtm ( Q )，但这种计算破坏了稀疏性。如果Q是稀疏的，那么计算一个基于Cholesky的稀疏平方根可能是值得的：

[ Qsqrt, p, S ] = chol( Q );

Qsqrt = Qsqrt * S;

有时候，有效的重新表述需要对问题等价的含义有实际的理解。例如，假设我们想在上面的目标中添加一个' 1正则项，由一些固定的、正的lambda加权：

minimize( sum_square( A * x - b ) + lambda * norm( x, 1 ) )

在这种情况下,我们通常不关心λ的特定的值;,而我们在一系列不同研究之间的权衡的剩余*取向和x的1-norm。相同的权衡可以通过检查这个修改模型研究:

minimize( norm( A * x - b ) + lambda2 * norm( x, 1 ) )

这是不完全相同的模型;λ和lambda2设置为相同的值不会产生相同的值(x)。但这两种模型跟踪相同的权衡曲线第二种形式可能会产生更精确的结果。

11.2双变量索引

在一些模型,约束的数量取决于模型参数不只是他们的大小。要建立这样的模型很简单在废用,Matlab for循环。为了分配这些约束一个单独的二元变量,我们必须找到一个方法来调整双变量的数量。出于这个原因,CVX支持索引双变量。

在现实中,他们只是标准Matlab细胞阵列的条目CVX双变量对象。让我们通过例子说明如何声明和使用索引双变量。考虑以下的半定规划SeDuMi例子:

 

这个问题最小化半正定矩阵的主对角线的加权和，同时保持每个对角线上的和不变。问题的参数为向量b∈Rn的元素，优化变量为对称矩阵X∈Rn × n。此模型的CVX版本是

cvx_begin 
    variable X( n, n ) symmetric
    minimize( ( n - 1 : -1 : 0 ) * diag( X ) );
    for k = 0 : n-1,
    sum( diag( X, k ) ) == b( k+1 ); 
    end
    X == semidefinite(n);
cvx_end

如果我们想要获得n个简单等式约束的对偶信息，我们需要一种方法来为for循环中的每个约束分配一个单独的对偶变量。具体如下：

cvx_begin
    variable X( n, n ) symmetric
    dual variables y{n} 
    minimize( ( n - 1 : -1 : 0 ) * diag( X ) );
    for k = 0 : n-1, sum( diag( X, k ) ) == b( k+1 ) : y{k+1}; 
    end 
    X == semidefinite(n);
cvx_end

语句对偶变量y { n }分配一个包含n个对偶变量的单元格数组，并将结果存储在Matlab变量Z中。for循环中的等式约束以y { k + 1 }为参考进行了增广，使得每个约束被分配一个单独的对偶变量。当发出cvx _ end命令时，CVX将计算这些对偶变量的最优值，并将它们存入n个单元数组y中。

这个例子固然有点简单化。经过仔细的安排，可以重写这个模型，以便将n个等式约束合并为一个向量约束，而这反过来又只需要一个向量对偶变量。1对于不适合这种简化的更复杂的示例，请参见文件

examples/cvxbook/Ch07_statistical_estim/cheb.m

在Cvx分布中。在这个问题中，for循环中的每个约束是一个线性矩阵不等式，而不是一个标量线性方程；因此，索引对偶变量是对称矩阵，而不是标量。

11.3 逐步逼近法

注意：如果您被CVX的警告消息引用到此网页：欢迎!请仔细阅读本节，充分理解为什么在CVX模型中使用log、exp等函数需要特别小心。

在1.2版之前，指数家族的函数exp、log、log _ det和其他函数不能在CVX中使用。直到最近，CVX使用了所谓的对称原/对偶求解器，这些求解器根本无法支持这些函数( 2 )。最近，诸如Mosek等求解器增加了支持。

对于指数锥。

对于不支持指数锥的求解器，我们构造了一个连续近似启发式，允许对称的原始/对偶求解器支持指数族函数。对该方法的精确描述超出了本文的范围，但大致来说，该方法的过程如下：

1 .选择一个初始近似中心点xc = 0。

2 .对每个log / exp /熵项构造多项式逼近，在xc的邻域内精确。

3 .求解这个近似模型得到它的最优点~ x。

4 .如果~ x满足原始模型达到足够精度的最优性条件，则退出。

5 .否则，将xc移向~ x，并重复步骤2 - 5。

再次，这是一种高度简化的描述方法；例如，我们实际上同时使用原解和对偶解来指导我们对xc和终止的判断。

这种方法对于许多问题已经被证明是非常有效的。然而，与许多启发式方法一样，它并不完美。即使对于已知有解决办法的问题，它有时也无法收敛。即使当它收敛时，由于它的迭代方法，它也比标准求解器慢几倍。因此，最好是谨慎和谨慎地使用它。以下是一些具体的使用技巧：

首先，如果您有权访问Mosek，请使用它，因为在版本9中添加了对指数锥的本机支持。

在许多情况下，完全等效的模型可以在没有它们的情况下构建，并且应该总是首选。例如，约束sum_log(x) >= 10

可以表达为geo_mean功能

geo_mean(x) >= log(10)^(1/length(x))

许多因素最大化问题通常使用log_det编写,但事实上,往往是不必要的。例如,考虑目标

minimize( log_det(X) )

CVX实际上把这个内部:

minimize( n*log(det_rootn(X)) )

所以你能做的只是把对数,而解决这个:

minimize( det_rootn(X) )

log_det(X)的值可以在模型完成后简单计算出来。不幸的是，这只有在log_det是目标中唯一的项时才有效；所以，例如，这个函数不能，不幸的是，以类似的方式转换。

minimize( log_det(X) + trace(C*X) )

-第三，尝试不同的求解器。SeDuMi的逐次逼近法往往比SDPT3更有效。因此，如果默认的求解器选择不能给你的模型一个解决方案，尝试切换到这些求解器中的一个。-

第三，尝试你的问题的小实例。如果它们在大实例失败的情况下成功了，那么至少你可以在考虑其他选项（如不同的求解器）之前确认模型的行为是否符合你的期望。

不幸的是，底线是我们不能保证逐次逼近法能成功处理你的特定模型。如果你遇到了问题，请你提交一份错误报告，但我们不能保证能修复。

11.3.1 抑制警告

由于所有这些注意事项，我们认为有必要在使用时发出警告，以便用户了解其实验性质。当你第一次试图在CVX中指定一个使用需要逐次逼近法的函数的模型时，这个警告就会出现。事实上，这个警告很可能把你带到本手册的这一部分。

如果你想在将来抑制这个警告，只需在构建模型前发出

cvx_expert true

命令即可。如果您希望在今后所有的MATLAB会话中抑制这一信息，请在这一命令之后再执行cvx_save_prefs命令。

11.4 幂函数和p值

为了实现幂函数xp的凸或凹分支以及p值的p值‖x‖p，CVX使用了[AG00]所述的SDP/SOCP转换方法的增强版。这种方法是精确的--只要指数p是有理的。为了确定积分值pn, pd，使pn/pd=p，CVX使用Matlab的rat函数，其默认公差为10-6。目前还没有办法改变这个公差。更多细节请参见MATLAB的rat函数文档。

所得模型的复杂性大致取决于值pn和pd的大小。让我们来介绍一下这种复杂性的更精确的衡量标准。对于p=2，一个约束xp≤y正好可以用一个2×2的LMI表示。

对于p = pn/pd的其他值，CVX会产生一些取决于pn和pd的2×2的LMI；我们用k(pn, pd)表示这个数字。 (在某些情况下还会产生额外的线性约束，但我们在此分析中忽略它们)。例如，对于p=3/1，我们有

 

 所以k（3，1）=2。一项经验研究表明，对于p = pn/pd > 1，我们有

 其中α(pn)项与log2项相比增长非常缓慢。事实上，对于pn≤4096，我们已经验证了α(pn)通常是1或2，但偶尔是0或3。在0<p<1和p<0的情况下也得到了类似的结果。

这种SDP表示法的成本对于几乎所有有用的p值来说都是比较小的。如果这个阈值不适合你，你可以使用命令cvx_power_warning(thresh)来改变它，其中thresh是所需的截止值。将阈值设置为Inf可以完全禁用它。和cvx_precision命令一样，你可以在一个模型内调用cvx_power_warning来改变单个模型的阈值；或者在一个模型外进行全局改变。该命令总是返回阈值的先前值，因此如果你愿意，你可以保存它并在完成模型后恢复它。您可以通过调用没有参数的 cvx_power_warning 来查询当前值。

11.5 过度确定的问题

当变量或集合中的结构没有被正确识别时，通常会出现过度确定的状态信息。例如，考虑寻找矩阵W∈Rn×n的最小对角线加法以使其成为正半定的问题。

CVX中，这个问题可能是表示如下:

n = size(W,1); 
cvx_begin 
    variable D(n,n) diagonal;
    minimize( trace( D ) ); 
    subject to 
        W + D == semidefinite(n);
cvx_end

如果我们将此规范应用于矩阵W=randn(5,5)，就会发出警告：

警告：等价约束过度；问题可能不可行。

变量cvx_status被设置为过度。这里发生的情况是，semidefinite(n)语句返回的未命名变量是对称的，但W是固定的、不对称的。因此，如上所述，该问题是不可行的。但这里还有n2个平等约束，而且只有n + n ∗ (n + 1)/2个唯一的自由度，因此问题是过度确定的。我们可以通过将平等约束替换为70 第11章 纠正这个问题。 sym( W ) + D == semidefinite(n); sym是我们提供的一个函数，可以提取其参数的对称部分；也就是说，sym(W)等于0.5 * ( W + W' )。

11.6 向原子库添加新函数

CVX允许定义新的凸函数和凹函数，并将其添加到原子库中，有两种方法，在本节中介绍。第一种方法很简单，CVX的很多用户都可以（也应该）使用，因为它只需要了解基本的DCP规则集。第二种方法非常强大，但有点复杂，应该被认为是一种高级技术，只有那些真正熟悉凸分析、严谨的凸编程和CVX当前状态的人才能尝试。

如果你已经实现了一个你认为对其他用户有用的凸或凹函数，请告诉我们；我们将很高兴在未来的版本中加入它。

11.6.1 通过DCP规则集的新函数

构建一个能在CVX中工作的新函数的最简单方法是使用完全符合DCP规则集的表达式来构建它。例如，考虑一下闭区间函数

 要在CVX中实现这个函数，只需创建一个包含函数

y = deadzone( x )

y = max( abs( x ) - 1, 0 ) 的deadzone.m文件。

这个函数的工作原理与你在CVX之外所期望的一样--也就是说，当它的参数是数值的时候。但是由于Matlab的运算符重载功能，如果调用一个仿射参数，它也会在CVX中工作。CVX将正确地得出结论，这个函数是凸的，因为所有进行的操作都符合DCP的规则：abs被认为是一个凸函数；我们可以从它那里减去一个常数，我们可以取结果和0的最大值，这就得到了一个凸函数。因此，我们可以在CVX规范中任何可能使用abs的地方自由使用deadzone，比如说，因为CVX知道它是一个凸函数。

我们要强调的是，以这种方式定义函数时，你使用的表达式必须符合DCP规则集，就像它们直接插入到CVX模型中那样。例如，如果我们用min代替max.

函数y = deadzone_bad( x )

y = min( abs( x ) - 1, 0 )

那么这个修改后的函数就不能满足DCP规则集。该函数在CVX规范之外也能工作，对于一个数字参数x，它能愉快地计算出min{|x|-1, 0}的值。但在CVX规范之内，如果用一个非常数参数调用，它将产生一个错误。

11.6.2 通过部分指定问题的新函数

在CVX中定义新函数的更高级方法依赖于以下凸分析的基本结果。

假设S⊂Rn×Rm是一个凸集，g : (Rn×Rm) → (R ∪+∞) 是一个凸函数。

那么f : Rn → (R ∪ +∞), f (x) , inf { g(x, y) | ∃y, (x, y) ∈S }也是一个凸函数。

(这个规则有时被称为部分最小化规则。)我们可以把凸函数f看作是凸优化问题系列的最优值，以x为索引或参数，最小化g(x, y)，服从(x, y)∈S，优化变量为y。

有一个特例应该非常熟悉：如果m = 1，g(x, y) , y，那么f (x) , inf { y | ∃y, (x, y) ∈S }就给出了f的经典表征：epi f = S + ({0} × R+) ，其中0∈Rn。

在CVX中，你可以用这种方式定义一个凸函数，即作为一个参数化的有规律的凸程序家族的最优值。我们把这种情况下的底层凸程序称为不完全规范--之所以这样称呼是因为在构建规范时参数（也就是函数输入）是未知的。不完全规范的概念起初看起来有点复杂，但它是非常强大的机制，使CVX能够支持各种各样的函数。

让我们看一个例子，看看它是如何工作的。考虑单位半宽的Huber惩罚函数h(x)：

 

我们可以用以下凸QP族来表达Huber函数，以x为参数：

 

我们注意到，这个QP中的目标函数和约束函数在v、w和x中是（共同）凸的。我们可以在CVX中实现Huber惩罚函数如下：

function cvx_optval = huber( x )
cvx_begin 
    variables w v;
    minimize( w^2 + 2 * v ); 
    subject to abs( x ) <= w + v;
    w <= 1; v >= 0;
cvx_end

如果huber被调用时有一个数字值x，那么在到达cvx_end语句时，CVX将找到一个完整的规范，并解决这个问题以计算结果。CVX将最佳目标函数值放入变量cvx_optval中，函数将该值作为其输出返回。当然，通过解QP来计算一个数值x的Huber函数是非常低效的。但它确实给出了正确的值（在核心求解器的精度范围内）。

然而，最重要的是，如果在CVX规范中使用Huber，并以仿生CVX表达式作为其参数，那么CVX将做正确的事情。特别是，CVX将识别出Huber函数，并以仿生参数调用，作为一个有效的凸表达式。在这种情况下，函数Huber将包含一个特殊的Matlab对象，在约束条件和目标中代表函数调用。因此，根据DCP规则集，函数huber可以用在任何可以使用传统凸函数的地方，在约束条件或目标函数中使用。

 

对于凹函数也有一个相应的发展。如上所述，给定一个凸集S，和一个凹函数g：(Rn × Rm) → (R ∪ -∞)，函数

 是凹的。如果g（x，y） ，y，那么

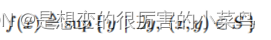
 给出f的超图表示：

在CVX中，凹形不完全规范是指使用最大化目标而不是最小化目标的规范；如果构建得当，它可以在CVX规范中的任何地方使用传统的凹形函数。

关于凹形不完全规范的例子，请看以下函数 

它的超图可以用一个线性矩阵不等式来表示：

 所以我们可以在CVX中实现这个函数如下：

function cvx_optval = lambda_min_symm( X )
n = size( X, 1 );
cvx_begin 
    variable y; 
    maximize( y ); 
    subject to X + X' - y * eye( n ) == semidefinite( n );
cvx_end

如果提供了一个X的数值，这个函数将返回min(eig(X+X'))（在数值公差范围内）。然而，这个函数也可以在CVX约束条件和目标中使用，就像原子库中的任何其他凹形函数。

在使用不完整规格定义函数时，有两个实际问题，我们将用上面的 huber 例子来说明这两个问题。首先，按照写法，这个函数只对标量值起作用。要把它（按元素）应用于一个向量，需要我们在for循环中遍历元素--这是一个非常低效的做法，特别是在CVX中。一个更好的方法是扩展 huber 函数来处理向量输入。事实上，这样做相当简单：我们只需创建一个多目标版本的问题。

function cvx_optval = huber( x )
sx = size( x ); 
cvx_begin 
    variables w( sx ) v( sx ); 
    minimize( w .^ 2 + 2 * v ); 
    subject to 
        abs( x ) <= w + v; 
        w <= 1; 
        v >= 0; 
cvx_end

这个版本的 huber 实际上将并行地创建问题的 sx "实例"；并且当用于 CVX 规范时，将被正确处理。

第二个问题是，如果huber的输入是数字，那么直接计算是一种比解决QP更有效的计算结果的方式。(更重要的是，多目标版本不能用于数字输入）。一个解决方案是将两个版本放在一个文件中，用一个适当的测试来选择要使用的正确版本。

function cvx_optval = huber( x ) 
if isnumeric( x ), 
    xa = abs( x ); 
    flag = xa < 1; 
    cvx_optval = flag .* xa.^2 + (~flag) * (2*xa-1); 
else, 
    sx = size( x ); 
    cvx_begin 
    variables w( sx ) v( sx ); 
    minimize( w .^ 2 + 2 * v ); 
    subject to 
        abs( x ) <= w + v; 
        w <= 1; v >= 0; 
    cvx_end
end

或者,您可以创建两个不同版本的函数,一个用于数字输入和一个用于CVX表达式,并将废版本在一个叫@cvx的子目录。(不包括这个目录在Matlab路径;只包括其母公司)。Matlab将自动调用@cvx目录中的版本,当其中一个参数是一个废变量。这是方法的版本huber CVX原子库中找到。

一个好方法学习更多关于使用不完整的规范是检查的一些例子已经在CVX原子库。不错的选择包括胡贝尔,inv_pos、lambda_min lambda_max, matrix_frac, quad_over_lin, sum_largest等等。一些有点难以阅读,因为诊断或错误检查代码,但这些都是相对简单的。