【思特奇杯·云上蓝桥-算法集中营】第3周

目录

目录

一、斐波那契数列

题干

斐波那契数，通常用 F(n) 表示，形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1 F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给你 n ，请计算 F(n) 。

解答

class Solution:
    def fib(self, n: int) -> int:
        if n < 2:
            return n
        
        p, q, r = 0, 0, 1
        for i in range(2, n + 1):
            p, q = q, r
            r = p + q
        
        return r

二、第N个泰波那契数

题干

泰波那契序列 Tn 定义如下：

T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2

给你整数 n，请返回第 n 个泰波那契数 Tn 的值

解答

class Solution:
    def tribonacci(self, n: int) -> int:
        if n == 0:
            return 0
        if n <= 2:
            return 1
        
        p = 0
        q = r = 1
        for i in range(3, n + 1):
            s = p + q + r
            p, q, r = q, r, s
        return s

三、爬楼梯

题干

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢

解答

class Solution {
public:
    int climbStairs(int n) {
        int p = 0, q = 0, r = 1;
        for (int i = 1; i <= n; ++i) {
            p = q; 
            q = r; 
            r = p + q;
        }
        return r;
    }
};

四、最小花费爬楼梯

题干

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费

解答

class Solution:
    def minCostClimbingStairs(self, cost: List[int]) -> int:
        n = len(cost)
        dp = [0] * (n + 1)
        for i in range(2, n + 1):
            dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
        return dp[n]

五、买股票的最佳时机

题干

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0

解答

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        inf = int(1e9)
        minprice = inf
        maxprofit = 0
        for price in prices:
            maxprofit = max(price - minprice, maxprofit)
            minprice = min(price, minprice)
        return maxprofit

六、最长公共子序列

题干

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

    例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列

解答

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        m, n = len(text1), len(text2)
        dp = [[0] * (n + 1) for _ in range(m + 1)]
        
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                if text1[i - 1] == text2[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1] + 1
                else:
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
        
        return dp[m][n]

七、杨辉三角

题干

 

解答

n = int(input(''))
m = []
for i in range(n):
    m.append([])
    for j in range(i+1):
        if j == 0 or i == j:
            m[i].append(1)
        else:
            m[i].append(m[i-1][j-1] + m[i-1][j])
    print(" ".join(str(a) for a in m[i]))

八、节点选择

题干

解答

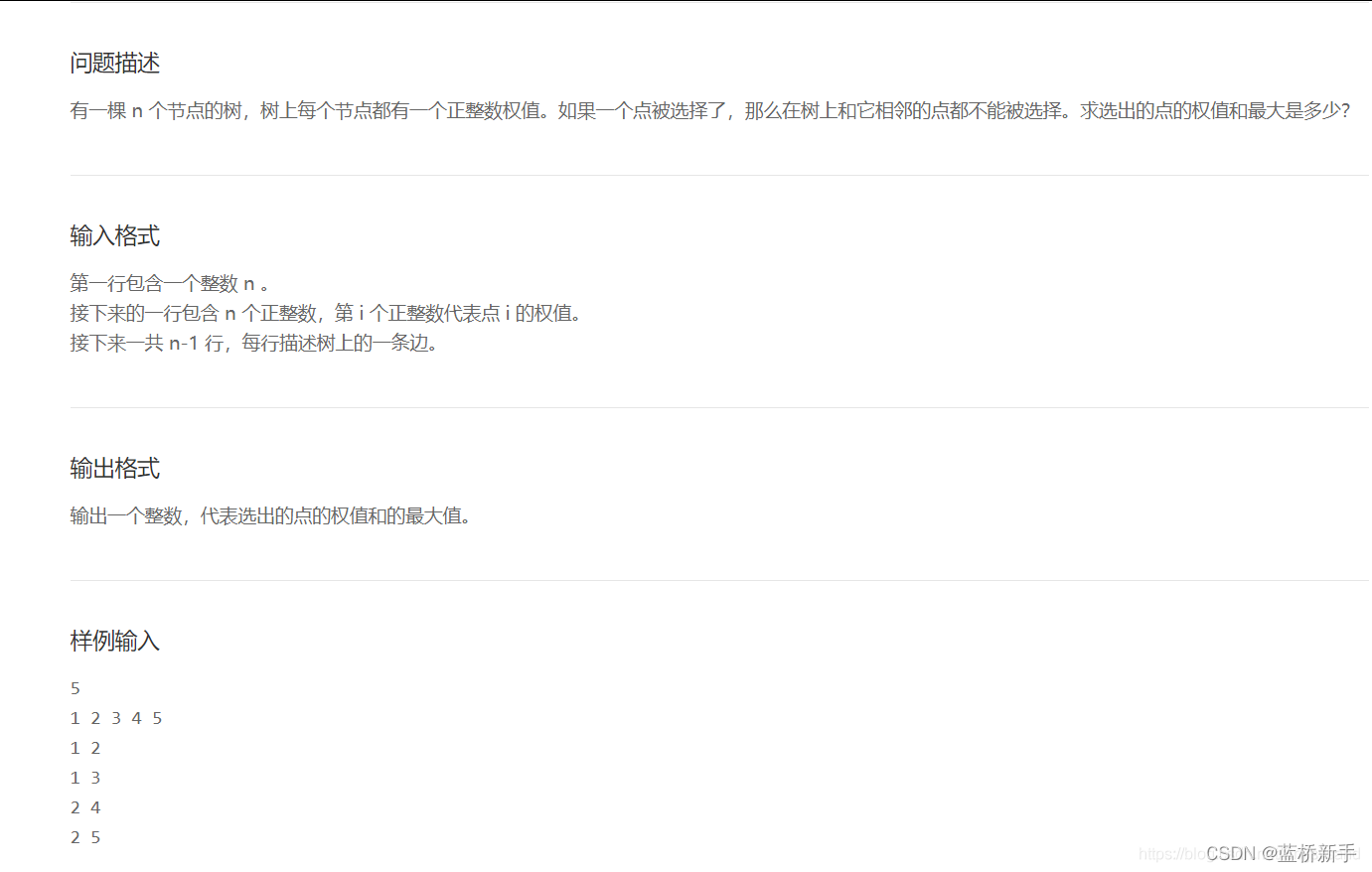
def dfs(node,pre):
    global value,table
    for i in table.get(node):
        if i !=pre:
            dfs(i,node)
            value[node][0]+=max(value[i][0],value[i][1])
            value[node][1]+=value[i][0]

def main():
    global value, table
    n = int(input())
    value = list(map(int, input().split()))
    value = list(map(lambda x:[0,x],value))
    value.insert(0,0)
    table = {}
    for i in range(n):
        table.update({i + 1: []})
    for i in range(n - 1):
        father, child = list(map(int, input().split()))
        table.get(father).append(child)
        table.get(child).append(father)
    print(table)
    dfs(1,0)
    print(max(value[1][0],value[1][1]))

if __name__=='__main__':
    main()

九、耐摔指数

题干

x 星球有很多高耸入云的高塔，刚好可以用来做耐摔测试。

塔的各层高度都是一样的。他们的第 1 层不是地面，而是相当于我们的 2 楼。

他们的地面层为 0 层。如果手机从第 7 层扔下去没摔坏，但第 8 层摔坏了，则

手机耐摔指数 = 7。

特别地，如果手机从第 1 层扔下去就坏了，则耐摔指数 = 0。

如果到了塔的最高层第 n 层扔没摔坏，则耐摔指数 = n。

为了加快测试进度，从每个型号手机中，抽样 3 部参加测试。

问题来了：如果已知了测试塔的高度 n，并且采用最佳的策略，在最坏的运气下

需要测试多少次才能确定手机的耐摔指数呢

 

解答

import sys
if __name__ == '__main__':
    phone = 3
    height = int(input())
    dp = [[0 for h in range(height)] for k in range(phone)]
    for h in range(height):
        dp[0][h] = h+1
    for k in range(phone):
        dp[k][0] = 1
    for h in range(1, height):
        for k in range(1, phone):
            minNum = sys.maxsize
            for t in range(1, h+1):
                minNum = min(minNum, 1 + max(dp[k-1][t-1], dp[k][h-t-1]))
            dp[k][h] = minNum

    print(dp[phone-1][height-1])

十、k好数

题干

如果一个自然数 N 的 K 进制表示中任意的相邻的两位都不是相邻的数字，那么

我们就说这个数是 K 好数。求 L 位 K 进制数中 K 好数的数目。例如 K = 4，L = 2

的时候，所有 K 好数为 11、13、20、22、30、31、33 共 7 个。由于这个数目很

大，请你输出它对 1000000007 取模后的值。

解答

#include<iostream>
#include<cmath>
using namespace std;
int dp[1000][1000];
const int MOD=1000000007;
int main()
{
	int sum=0;
	int CountK(int,int,int);
	int K,L;
	cin>>K>>L;
	if(K==1&&L==1)	//
		cout<<0<<endl;
	else if(K>1&&L==1)// 
		cout<<K<<endl;
	else if(L>1)
	cout<<CountK(L,K,sum)<<endl;
	return 0;
}
int CountK(int length,int range,int sum)
{
	for(int i=1;i<range;i++)
	{
		dp[0][i]=1;
	}
	for(int i=1;i<length;i++)
	{
		for(int j=0;j<range;j++)
		{
			for(int k=0;k<range;k++)
			{
				if(abs(j-k)!=1)
				{
					if((j-1)==0&&k==0)//
						continue;
					dp[i][j]=dp[i][j]+dp[i-1][k];
					dp[i][j]%=MOD;
				}
			}
		}
	}
	for(int i=0;i<range;i++)
	{
		sum+=dp[length-1][i];
		sum%=MOD;
	}
	return sum;
}

---