双指针解链表

双指针解链表

环形链表（8）

图解

假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点 节点数为y。 从相遇节点 再到环形入口节点节点数为 z。 如图所示：

相遇时： slow指针走过的节点数为: x + y

fast指针走过的节点数：x + y + n (y + z)，n为fast指针在环内走了n圈才遇到slow指针， （y+z）为 一圈内节点的个数A。

因为fast指针是一步走两个节点，slow指针一步走一个节点， 所以 fast指针走过的节点数 = slow指针走过的节点数 * 2：

(x + y) * 2 = x + y + n (y + z)

将x单独放在左面：x = n (y + z) - y ,

x = (n - 1) (y + z) + z 注意这里n一定是大于等于1的，因为 fast指针至少要多走一圈才能相遇slow指针。

先拿n为1的情况来举例，意味着fast指针在环形里转了一圈之后，就遇到了 slow指针了。

当 n为1的时候，公式就化解为 x = z

从头结点出发一个指针，从相遇节点 也出发一个指针，这两个指针每次只走一个节点， 那么当这两个指针相遇的时候就是 环形入口的节点。

思路

1.判断是否有环

​ 2.有环则从头指针一个节点与相遇节点出发一个指针，两个指针相遇就是环形入口x = z

代码

``

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) {// 有环
                ListNode index1 = fast;
                ListNode index2 = head;
                // 两个指针，从头结点和相遇结点，各走一步，直到相遇，相遇点即为环入口
                while (index1 != index2) {
                    index1 = index1.next;
                    index2 = index2.next;
                }
                return index1;
            }
        }
        return null;
    }
}

删除链表的倒数第n个节点（19）

思路

1.创建虚拟指针ListNode dummy=new ListNode(-1,head);防止删除的是头节点

2.让快慢指针指向虚拟指针ListNode fast=dummy; ListNode slow=dummy;

3.让快指针先走n+1步

for(int i=0;i<=n;i++){ fast=fast.next; }

4.快慢指针一起走

5.当快指针为空的时候，慢指针正好指向倒数第n个节点的前一个节点

代码

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dummy=new ListNode(-1,head);
        ListNode fast=dummy;
        ListNode slow=dummy;
        for(int i=0;i<=n;i++){
            fast=fast.next;
        }
        while(fast!=null){
            slow=slow.next;
            fast=fast.next;
        }
        slow.next=slow.next.next;
        // ListNode ans=dummy.next;
        return dummy.next;
	          
	}
}

反转链表204

图解

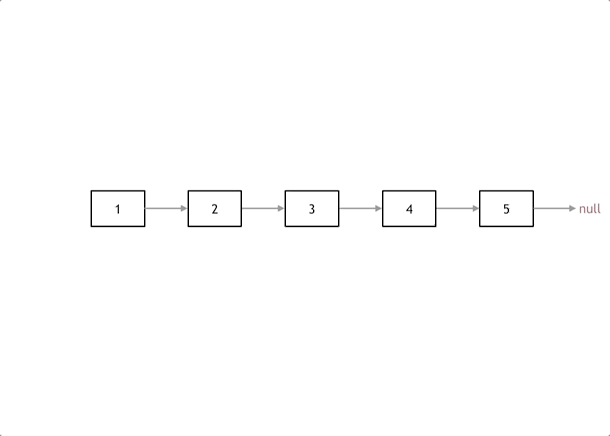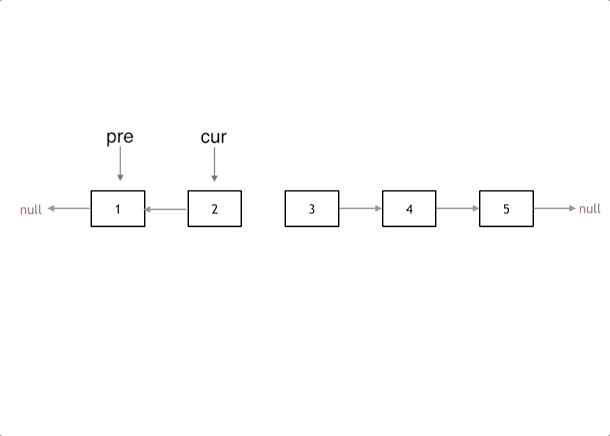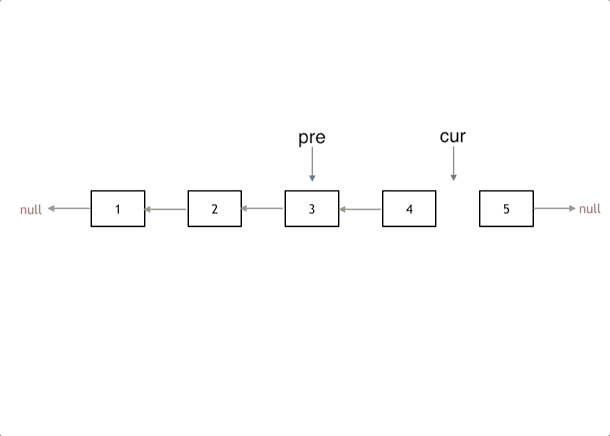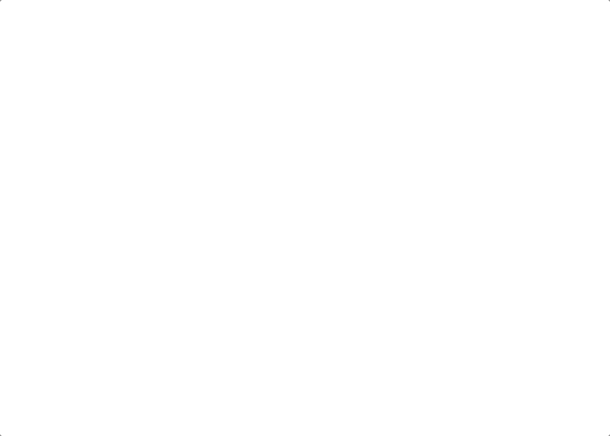
思路

1. 定义一个cur指针，指向头结点，再定义一个pre指针，初始化为null
2. 把 cur.next 节点用tmp指针保存一下 ， cur.next 指向pre

代码

class Solution {
	public ListNode reverseList(ListNode head) {
		//申请节点，pre和 cur，pre指向null
		ListNode pre = null;
		ListNode cur = head;
		ListNode tmp = null;
		while(cur!=null) {
			//记录当前节点的下一个节点
			tmp = cur.next;
			//然后将当前节点指向pre
			cur.next = pre;
			//pre和cur节点都前进一位
			pre = cur;
			cur = tmp;
		}
		return pre;
	}
}