冒泡排序（关于排序算法的重要性）

我们介绍一下冒泡排序，对于少量的元素排序，他是一个有效的算法。高效且稳定的排序算法在武学上被称为“秘笈”，而像冒泡排序这样的算法，因为易学、易懂、易用，成了流行品种。当然，他是不是一个高效有用的算法，不取决于他是否流行。

我们举一个简单的例子，我们让运行冒泡排序的的一台较快的计算机（计算机A）与运行归并排序的一台较慢的计算机（计算机B）竞争。每台计算机必须排序一个具有1000万个数的数组。（虽然1000万个数似乎很多，但别忘了，我们是一个14亿的人口大国，这样看来，1000万似乎就算不上很大了，如果这些数字是8字节的数据，那么输入将占用大致80MB）假设计算机A每秒执行百亿条指令（几乎快于任何单台穿行计算机），而计算机B每秒仅仅执行1000万条指令，结果计算机A就纯计算能力来说比计算机B快1000倍。为了使差别；更具有戏剧性，假设世界上最厉害最灵性的程序员用计算机A编码冒泡排序，而为了排序n个数，计算机A需要执行n^2条指令。进一步假设有一位水平一般的程序员使用计算机B编码归并排序，结果代码需要执行nlgn（以2为底的对数）。为了排序1000万个数，计算机A需要：

通过使用一个运行时间的增长较慢的算法，即使采用一个较差的编译器，计算机B比计算机A还快将近100倍！当排序超过一亿时，归并排序的优势更加明显。

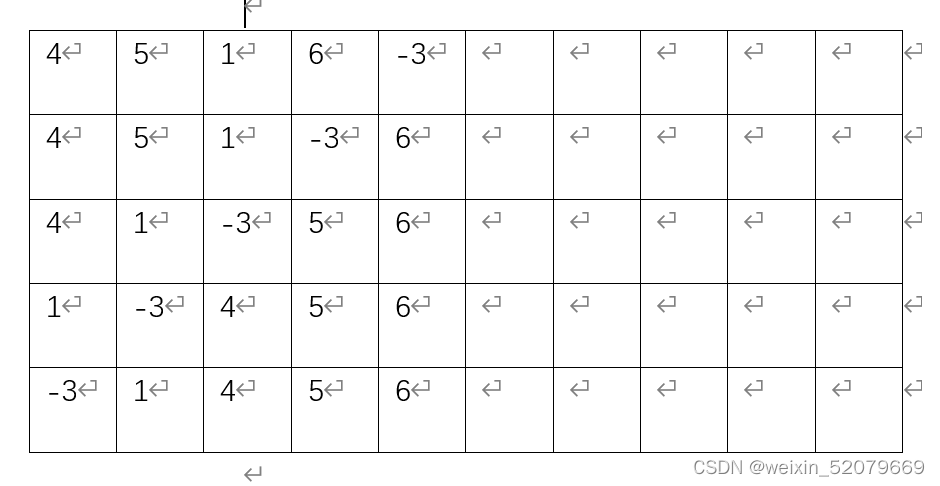
再说说冒泡排序的排序方法，首先用数组中的第一个数跟后面的数比较，如果比后面的数大，则交换位置，直到比较完一次，我们找到了最大的数排在数组的最后一个位置。之后我们用同样的方法，从第一个数开始比较到倒数第二个数，最后一个数因为是最大的，所以不用比较，第二轮我们找到了第二大的数，放在倒数第二的位置，于此类推循环n-1次。

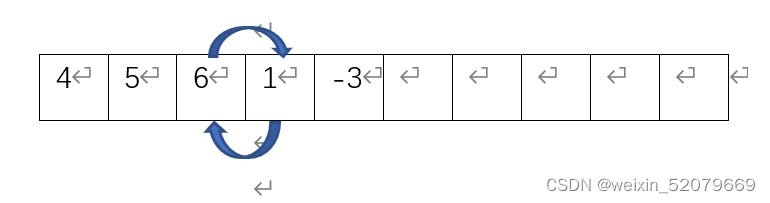
首先4和5比，4比5小，所以不交换位置

然后5和6比，同样不交换位置

之后6和1比，1比6小，1和6交换位置

然后到-3和6比，然后交换位置

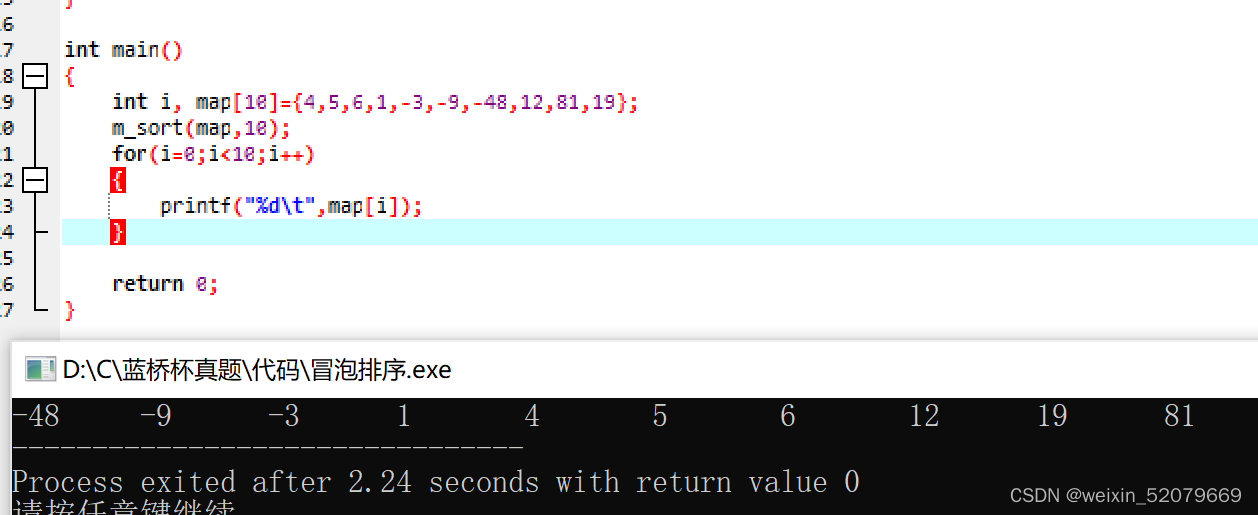
代码印证

#include <stdio.h>
void m_sort(int a[], int n)
{
	int i, j, temp;
	for (j = 0; j < n - 1; j++)
	for (i = 0; i < n - 1 - j; i++)
	{
		if (a[i] > a[i + 1])
		{
			temp = a[i];
			a[i] = a[i + 1];
			a[i + 1] = temp;
		}
	}
}

int main()
{
	int i, map[10]={4,5,6,1,-3,-9,-48,12,81,19};
	m_sort(map,10);
	for(i=0;i<10;i++)
	{
		printf("%d\t",map[i]);
	}
	
	return 0;
}

谢谢大家！