LeetCode每日一题（23）——最大三角形面积

1.题目

给定包含多个点的集合，从其中取三个点组成三角形，返回能组成的最大三角形的面积。

2.示例

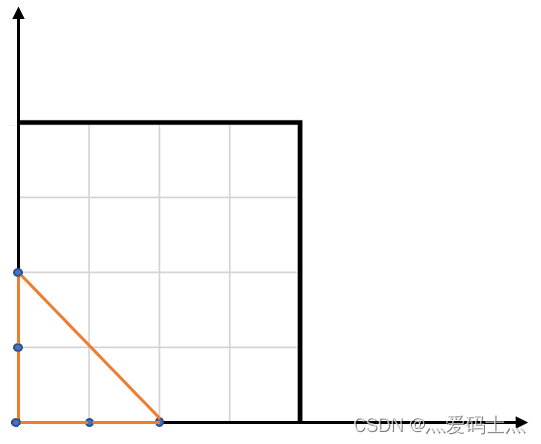
输入: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
输出: 2
解释: 这五个点如下图所示。组成的橙色三角形是最大的，面积为2。

注意:

   3 <= points.length <= 50. 
  不存在重复的点。 
  -50 <= points[i][j] <= 50. 
  结果误差值在10^-6 以内都认为是正确答案。

3.思路

感觉这道题并不简单，但是标的难度是简单，也就是说暴力可以通过。所以直接暴力穷举所有可能的情况，通过公式计算每一组的面积。保留最大的结果最后返回即可。如果对于时间复杂度有要求还是要用凸包解决。附官方的凸包解法代码。

4.代码

暴力穷举

func triangleArea(x1, y1, x2, y2, x3, y3 int) float64 {
    return math.Abs(float64(x1*y2+x2*y3+x3*y1-x1*y3-x2*y1-x3*y2)) / 2
}

func largestTriangleArea(points [][]int) (ans float64) {
    for i, p := range points {
        for j, q := range points[:i] {
            for _, r := range points[:j] {
                ans = math.Max(ans, triangleArea(p[0], p[1], q[0], q[1], r[0], r[1]))
            }
        }
    }
    return
}

凸包

func cross(p, q, r []int) int {
    return (q[0]-p[0])*(r[1]-q[1]) - (q[1]-p[1])*(r[0]-q[0])
}

func getConvexHull(points [][]int) [][]int {
    n := len(points)
    if n < 4 {
        return points
    }

    // 按照 x 从小到大排序，如果 x 相同，则按照 y 从小到大排序
    sort.Slice(points, func(i, j int) bool { a, b := points[i], points[j]; return a[0] < b[0] || a[0] == b[0] && a[1] < b[1] })

    hull := [][]int{}
    // 求凸包的下半部分
    for _, p := range points {
        for len(hull) > 1 && cross(hull[len(hull)-2], hull[len(hull)-1], p) <= 0 {
            hull = hull[:len(hull)-1]
        }
        hull = append(hull, p)
    }
    // 求凸包的上半部分
    m := len(hull)
    for i := n - 1; i >= 0; i-- {
        for len(hull) > m && cross(hull[len(hull)-2], hull[len(hull)-1], points[i]) <= 0 {
            hull = hull[:len(hull)-1]
        }
        hull = append(hull, points[i])
    }
    // hull[0] 同时参与凸包的上半部分检测，因此需去掉重复的 hull[0]
    return hull[:len(hull)-1]
}

func triangleArea(x1, y1, x2, y2, x3, y3 int) float64 {
    return math.Abs(float64(x1*y2+x2*y3+x3*y1-x1*y3-x2*y1-x3*y2)) / 2
}

func largestTriangleArea(points [][]int) (ans float64) {
    convexHull := getConvexHull(points)
    n := len(convexHull)
    for i, p := range convexHull {
        for j, k := i+1, i+2; j+1 < n; j++ {
            q := convexHull[j]
            for ; k+1 < n; k++ {
                curArea := triangleArea(p[0], p[1], q[0], q[1], convexHull[k][0], convexHull[k][1])
                nextArea := triangleArea(p[0], p[1], q[0], q[1], convexHull[k+1][0], convexHull[k+1][1])
                if curArea >= nextArea {
                    break
                }
            }
            ans = math.Max(ans, triangleArea(p[0], p[1], q[0], q[1], convexHull[k][0], convexHull[k][1]))
        }
    }
    return
}