深度学习笔记2_梯度性质证明深度学习-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_51828505/article/details/143212204

1.梯度的数学原理和性质

在梯度下降算法中，我们需要让函数的自变量沿函数梯度的反方向运动，使函数值以最快的速度减小，从而找到目标函数的极小值。

梯度（gradient),是多元函数全部偏导数所构成的向量。使用 $\bigtriangledown$ 表示某个函数的梯度。函数上某个点沿着梯度的方向运动，函数增加的速度最快，沿着梯度的反方向运动，函数减小的最快。梯度向量是在函数的输入空间中定义的，函数f(x,y)输入空间在平面x-O-y上

$f(x,y)=x^{2}+y^{2}$

$\frac{\partial f }{\partial x}=\frac{\partial }{\partial x}(x^{2}+y^{2})=2x$ $\bigtriangledown f(x,y)=(2x,2y)$

$\frac{\partial f}{\partial y}={\frac{\partial }{\partial y}}(x^{2}+y^{2})=2y$

2.梯度下降算法

梯度下降算法的目标：求解目标函数的极值点。

求函数极小值的方法：1.求偏导数的数学方法。2.循环迭代的梯度下降算法

执行梯度下降算法时，算法会一点点调整x0,x1的值使f(x)变小，一直到达某个局部最小值。开始时先对x0和x1初始化，随意设置一个初始值，然后寻找到函数最低点的路径，行进前需要选择行进的方向，A点周围360度有无数方向，选择一个能使函数值迅速下降的方向作为前进方向，才能找到极小值。而这个方向就是改位置的梯度的反方向。

计算出负梯度后，沿着该方向走一小步，所谓一小步就是基于梯度的反方向，略微修改x0和x1的值，不断按照这样的步骤调整自变量，函数f(x)就会不断减小，最终到达函数的最低点。

，

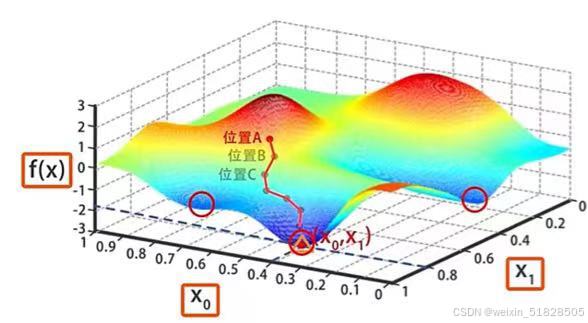
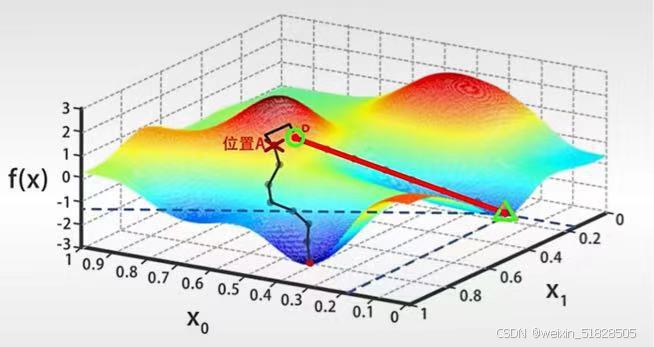
需要注意的是，这个位置（图中极小值点，即 $\bigtriangleup$ 标注的位置）很可能不是函数的全局最小值，但肯定是从位置A出发，能够一点一点找到的局部最小值。如果一开始初始化的时候，不选择A，而是另外的P点，在这个基础上进行梯度下降搜索，很可能找到另外一个局部最优解。

Python实现f(x,y)=x^2,y^2极小值的梯度下降算法：

x = 1.1  # 随意设置自变量x的初始值
y = 2.1  # 随意设置自变量x的初始值
n = 100  # 设置迭代轮数
alapa = 0.05  # 迭代速率，alapa用于控制“一小步”的大小
for i in range(1, n + 1):  # 梯度下降是一个迭代的过程，对应于for循环
    # 在循环中会一步步调整自变量的取值，让函数不断减小
    # gx和gy用于控制迭代的方向
    gx = x * 2  # f(x,y)对x的偏导
    gy = y * 2  # f(x,y)对y的偏导

    x = x - alapa * gx  # x方向的一小步
    y = y - alapa * gy  # y方向的一小步
    # 计算过后,自变量(x,y)沿着负梯度方向，移动一小步
    print(f'第{i}轮迭代后,'  # 迭代轮数i
          f'x={x:.3f},'  # 自变量x
          f'y={y:.3f},'  # 自变量y 
          f'f(x,y)={x ** 2 + y ** 2:.3f}') #函数值f(x,y)

第1轮迭代后,x=0.990,y=1.890,f(x,y)=4.552
第2轮迭代后,x=0.891,y=1.701,f(x,y)=3.687
第3轮迭代后,x=0.802,y=1.531,f(x,y)=2.987
第4轮迭代后,x=0.722,y=1.378,f(x,y)=2.419
第5轮迭代后,x=0.650,y=1.240,f(x,y)=1.960
第6轮迭代后,x=0.585,y=1.116,f(x,y)=1.587
第7轮迭代后,x=0.526,y=1.004,f(x,y)=1.286
第8轮迭代后,x=0.474,y=0.904,f(x,y)=1.041
第9轮迭代后,x=0.426,y=0.814,f(x,y)=0.844
……
会一直打印到第100轮，这里不再写了

梯度下降算法不一定找到目标函数的全局最小值，但一定可以找到某个局部最小值，这与目标函数f(x)本身的数学性质有关。如果函数是凸函数，梯度下降算法可以保证求出全局最小值。如果函数是非凸的，梯度下降算法可能只求出某个局部最小值。

3.一元函数的梯度下降算法

求f(x)取得极小值时x的取值：

1.设置自变量的初始值，求导数计算x的梯度

2.计算自变量步长

3.沿着梯度反方向调整自变量的值。

#使用梯度下降，求二次函数f(x)极值的代码实现
x=2#初始自变量的值
alapha=0.001#迭代速率
iteration=10#迭代次数
for i in range(1,iteration+1):
    gradient=2*x-2#函数导数，求梯度
    step=alapha*gradient#计算每次迭代的步长
    x=x-step
    print(f'第{i}次迭代，x={x:.3f},梯度gradient={gradient:.3f}')

4.梯度下降迭代速率

在使用梯度下降对参数进行迭代时，需要使用常量 $\alpha$ ，来控制以多大的幅度更新参数x，使得用更少的迭代次数获得最优解。每次进行梯度下降时，使用x=x- $\alpha$ *f'(x),对x更新，迭代速率 $\alpha$ 在选择时，需要选择一个不大不小合适的值才能使梯度下降正常进行。

$\alpha$ 一般取值范围在（0.0001，0.001）之间，如果f(x)比较光滑， $\alpha$ 就大一点，如果f(x)在某些区域的导数变化剧烈， $\alpha$ 就小一点才能使迭代更稳定。

移动幅度 $\alpha$ *f'(x)会随着迭代的次数越来越小，x越接近极值点，导数f'(x)会变得更小，梯度下降算法就会采取更小的移动幅度。现阶段学习中先不考虑需要额外调整学习速率 $\alpha$ 的值，之后的学习中会遇到需要调整学习速率 $\alpha$ 的情况。

5.Pytorch求偏导数

pytorch的自动微分是一种自动计算导数和梯度的技术。自动微分依赖链式法则。通过backward函数自动计算梯度。

import torch
import matplotlib.pyplot as plot
if __name__=='__main__':
    #生成自变量序列x,张量x,需要自动微分功能
    #这里requires_grad=True代表张量x需要自动微分功能
    x=torch.linspace(-10,10,100,requires_grad=True)
    y_f=x*x+2*x-4#计算函数f(x)的值

    #使用backward函数，计算f(x)关于x的梯度 ，所有的梯度值，都会保存在x.grad中
    y_f.sum().backward()
    print(y_f)
    print(y_f.sum())
    print(x.grad)
    #因为backward()函数只能对标量进行操作，所以需要先使用y_f.sum,将y_f中的元素求和
    #将其转换为一个标量，再在这个标量上调用backward,计算梯度
    #将梯度值x.grad、函数值y_f、自变量x,从pytorch张量转换为numpy数组
    #转换前需要使用detach,他会创建一个原张量的副本
    y_df=x.grad.detach().numpy()
    y_f=y_f.detach().numpy()
    x=x.detach().numpy()
    #使用detach将正常的张量转换为numpy数组后，不会影响自动梯度的计算

    #绘制图像
    plot.plot(x,y_f,label='f(x)=x*x+2*x-4')
    plot.plot(x,y_df,label='df(x)=2*x+2')
    plot.legend()#对图像进行标记
    plot.grid(True)#使用grid函数标记出网格线
    plot.show()

grad.zero_方法

grad.zero_方法用于将张量中的梯度清零，是梯度下降过程中必须要调用的方法。如果要重复调用backward,需要先调用grad.zero_将张量中的梯度清零。

import torch
#初始化一个带有梯度的张量
x=torch.tensor([0.0],requires_grad=True)
y=x*x+2*x-4
y.backward()#调用backdraw计算y关于x的梯度
df=2*x+2
print("第一次打印：")
print("x的值：",x.data)
print("x的梯度：",x.grad.data)
print("x的梯度值：",df.data)
print()
x.grad.zero_()
y=x*x+2*x-4
y.backward()
print("第二次打印：")
print("x的值：",x.data)
print("x的梯度：",x.grad.data)
print("x的梯度值：",df.data)
print()
y=x*x+2*x-4
y.backward()
print("第三次打印：")
print("x的值：",x.data)
print("x的梯度：",x.grad.data)
print("x的梯度值：",df.data)

第一次打印：
x的值： tensor([0.])
x的梯度： tensor([2.])
x的梯度值： tensor([2.])

第二次打印：
x的值： tensor([0.])
x的梯度： tensor([2.])
x的梯度值： tensor([2.])

第三次打印：
x的值： tensor([0.])
x的梯度： tensor([4.])
x的梯度值： tensor([2.])

第三次打印时因为第二次计算梯度后，没有使用grad.zero_对张量中的梯度清零，所以梯度累加到了已有的梯度上。所以如果需要重新计算梯度值，需要将原来保存的梯度清零。

使用pytorch求 $f(x,y)=x^{_{2}}+y^{_2{}}$ 的偏导，对梯度下降算法代码进行改进。

import torch
x=torch.tensor([1.1],requires_grad=True)
y=torch.tensor([1.1],requires_grad=True)
n =100
alpha=0.05
for i in range(1,n+1):
    z=x*x+y*y
    z.backward()#调用backward计算梯度
    #更新x.data和y.data,进行梯度下降算法
    x.data-=alpha*x.grad.data
    y.data-=alpha*y.grad.data
    #清楚梯度
    x.grad.zero_()
    y.grad.zero_()
    print(f'第{i}轮迭代后,'  # 迭代轮数i
              f'x={x.item():.3f},'  # 自变量x
              f'y={y.item():.3f},'  # 自变量y 
              f'f(x,y)={z.item():.3f}') #函数值f(x,y)