算法集训营 - Day2 | 209.长度最小的子数组，59.螺旋矩阵II，区间和

209.长度最小的子数组

题目

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。

示例：

输入：s = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

核心思路

大前提：都是正整数
如果有复数就可以不可以用滑动窗口，因为负数收缩还是扩展窗口，总和可能增加或者减少，变得不可控。

• 滑动窗口概念
  滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。
  本质是满足单调性，即左右指针只往一个方向走且不会回头，收缩的本质是去掉不再需要的元素。

在本题中实现滑动窗口，主要确定如下三个重点：

• 窗口内是什么？
  满足其和 ≥ s 的长度最小的 连续 子数组。
• 如何移动窗口的起始位置？
  如果当前窗口（集合里的元素）的值大于等于s了，窗口就要向前移动了（也就是该缩小了）。
• 如何移动窗口的结束位置？
  窗口的结束位置就是遍历数组的指针，也就是for循环里的索引j。

解题过程

实现代码：

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int i = 0; //起始指针
        int sum = 0;
        int result = Integer.MAX_VALUE; //为最大值才能进行比较
        for (int j = 0; j < nums.length; j++) { //j为终止指针
            sum += nums[j];
            while (sum >= target) {   //此处不可用if，下文有解释
                result = Math.min(result, j-i+1); 
                sum -= nums[i++]; //移动起始位置
            }
        }
        return result == Integer.MAX_VALUE ? 0 : result;
    }
}

• 时间复杂度：O(n)

实现代码注意点：

• result应该初始为最大值，只有取最大值，才会在min(result, subL)中不断更新

• 集合收集完后，要开始移动起始位置，向后移动一位，即sum和减去nums[j]

• 要用while(sum >= s) 而不是if (sum >= s) 因为是持续向后移动的过程，往后移动一位可能sum还是大于s的，知道元素集合小于s为止。如果是if，执行一次就结束了。

59.螺旋矩阵

题目

给定一个正整数 n，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。

示例:

输入: 3 输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]

核心思路

坚持循环不变量原则，重点在解决边界问题，即在代码处理上，坚持左闭右开，或者左开右闭。

模拟顺时针画矩阵的过程:

• 填充上行从左到右
• 填充右列从上到下
• 填充下行从右到左
• 填充左列从下到上

解题过程

实现代码：

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] nums = new int[n][n];
        int startX = 0, startY = 0; // 起点
        int offSet = 1;
        int count = 1;
        int loop = 1; //圈数
        int i,j;
        while (loop <= n/2) { //顶部
            for (j = startY; j < n - offSet; j++) { //左闭右开
                nums[startX][j] = count++;
            }
            for (i = startX; i < n - offSet; i++) { //右边
                nums[i][j] = count++;
            }
            for ( ; j > startY; j--) { //底部
                nums[i][j] = count++;
            }
            for ( ; i > startX; i--) { //左边
                nums[i][j] = count++;
        }
        startX++;
        startY++;
        offSet++;
        loop++;
        }
        if (n % 2 == 1) { //n为奇数时，单独赋值给中间
            nums[startX][startY] = count;
        }
        return nums;
    }
}

• 时间复杂度 O(n^2): 模拟遍历二维矩阵的时间
• 空间复杂度 O(1)

区间和

题目

给定一个整数数组 Array，请计算该数组在每个指定区间内元素的总和。

• 输入描述
  第一行输入为整数数组 Array 的长度 n，接下来 n 行，每行一个整数，表示数组的元素。随后的输入为需要计算总和的区间，直至文件结束。

• 输出描述
  输出每个指定区间内元素的总和。

输入示例

5
1
2
3
4
5
0 1
1 3

输出示例

3
9

核心思路

在这道题中，暴力解法会超时。

在涉及计算区间和的问题时，前缀和非常有用！

前缀和概念
举例说明：我们要统计 vec[i] 这个数组上的区间和。

我们先做累加，即 p[i] 表示 下标 0 到 i 的 vec[i] 累加 之和

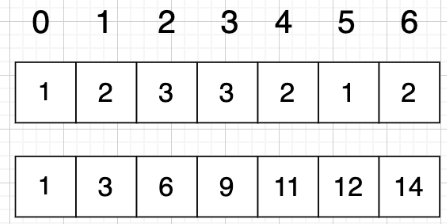
第一列为vec[i]，第二列为p[i]
在vec数组上 下标 2 到下标 5 之间的累加和，那是不是就用 p[5] - p[1] 就可以

• 为什么？
  p[1] = vec[0] + vec[1];
  p[5] = vec[0] + vec[1] + vec[2] + vec[3] + vec[4] + vec[5];
  p[5] - p[1] = vec[2] + vec[3] + vec[4] + vec[5];

实现代码

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        int n = scanner.nextInt();
        int[] vec = new int[n];
        int[] p = new int[n];

        int presum = 0;
        for (int i = 0; i < n; i++) {
            vec[i] = scanner.nextInt();
            presum += vec[i];
            p[i] = presum;
        }

        while (scanner.hasNextInt()) {
            int a = scanner.nextInt();
            int b = scanner.nextInt();

            int sum;
            if (a == 0) {
                sum = p[b];
            } else {
                sum = p[b] - p[a - 1];
            }
            System.out.println(sum);
        }

        scanner.close();
    }
}