无线电能传输（WPT）系统中S-P拓扑的详细参数计算步骤

兀兀年

已于 2025-01-24 22:46:07 修改

阅读量855

点赞数 9

文章标签：硬件工程

于 2025-01-24 22:32:48 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.youkuaiyun.com/weixin_51676207/article/details/145347332

版权

目录

1. 系统参数定义

2. 谐振条件推导

2.1 发射端谐振条件

2.2 接收端谐振条件

3. 输入输出关系推导

3.1 输入电压与输入电流的关系

3.2 输出电压与输出电流的关系

3.3 互感耦合关系

4. 求解输入电流 I1 和输出电流 I2

5. 输出电压 UL

1. 系统参数定义

输入电压（Uin）：系统的输入电压。
输出电压（UL）：负载上的输出电压。
输入电流（I1）：发射端的输入电流。
输出电流（I2）：接收端的输出电流。
负载电阻（Req）：负载电阻。
工作频率（f）：系统的工作频率。
角频率（ω）：ω=2πf。
发射线圈电感（L1）：发射端的电感。
接收线圈电感（L2）：接收端的电感。
互感（M）：发射线圈和接收线圈之间的互感。

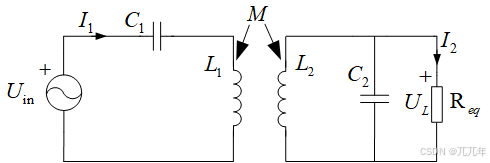
2. 谐振条件推导

2.1 发射端谐振条件

发射端为串联谐振电路，其阻抗为：

$Z_1=j\omega L_1+\frac{1}{j\omega C_1}$

在谐振时，电感和电容的阻抗相互抵消，即：

$\omega L_1=\frac{1}{\omega C_1}$

解得发射端电容：

$C_1=\frac{1}{\omega^2L_1}$

2.2 接收端谐振条件

接收端为并联谐振电路，其阻抗为：

$Z_2=\frac{1}{j\omega C_2+\frac{1}{j\omega L_2}}$

在谐振时，电感和电容的阻抗相互抵消，即：

$\omega L_2=\frac{1}{\omega C_2}$

解得接收端电容：

$C_2=\frac{1}{\omega^2L_2}$

3. 输入输出关系推导

3.1 输入电压与输入电流的关系

在谐振条件下，发射端的阻抗为纯电阻，输入电压与输入电流的关系为：

$U_{in}=I_1\cdot Z_1$

由于 Z1 在谐振时为纯电抗（Z1=0），输入电流 I1由系统的耦合和负载决定。

3.2 输出电压与输出电流的关系

在接收端，输出电压 UL与输出电流 I2的关系为：

$U_L=I_2\cdot R_{eq}$

3.3 互感耦合关系

发射端和接收端通过互感 M 耦合，其电压关系为：(基尔霍夫电压电流定律)

$U_{in}=j\omega L_1I_1+j\omega MI_2$

$0=j\omega MI_1+j\omega L_2I_2+I_2R_{eq}$

4. 求解输入电流 I1 和输出电流 I2

从互感耦合关系中，可以得到以下方程组：

$U_{in}=j\omega L_1I_1+j\omega MI_2\quad(1)$

$0=j\omega MI_1+j\omega L_2I_2+I_2R_{eq}\quad(2)$

从方程 (2) 中解出 I2：

$I_2=-\frac{j\omega MI_1}{j\omega L_2+R_{eq}}$

将 I2代入方程 (1)：

$U_{in}=j\omega L_1I_1+j\omega M\left(-\frac{j\omega MI_1}{j\omega L_2+R_{eq}}\right)$

化简：

$U_{in}=j\omega L_1I_1-\frac{\omega^2M^2I_1}{j\omega L_2+R_{eq}}$

进一步化简：

$U_{in}=I_1\left(j\omega L_1-\frac{\omega^2M^2}{j\omega L_2+R_{eq}}\right)$

解得输入电流 I1：

$I_1=\frac{U_{in}}{j\omega L_1-\frac{\omega^2M^2}{j\omega L_2+R_{eq}}}$

输出电流 I2：

$I_2=-\frac{j\omega MI_1}{j\omega L_2+R_{eq}}$

5. 输出电压 UL

输出电压 UL 为：

$U_L=I_2\cdot R_{eq}$

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。