树和二叉树

树就是一种非线性的数据结构，存储的是具有“一对多”关系的数据元素的集合。类似现实生活中的树（倒置的树），所以称这种存储结构为“树型”存储结构，可以用于保存组织架构、图书目录等数据。

树（tree）是 n(n≥0)个节点的有限集。当n=0时，称为空树。

树的节点

树的结点：使用树结构存储的每一个数据元素都被称为“结点”。如下图，数据元素 123 都是树中的一个结点；而节点又根据不同的条件被分为根节点、子节点、叶子节点三种；我们可以根据下图来理解各种节点：

• 根节点：节点1是根节点（root），在非空树中，根节点就是没有父节点的节点，并且是唯一的；
• 子节点：节点2、节点3是根节点的子节点，简单来说，就是与根节点直接相连的那些节点；
• 叶子节点：节点5、节点6、节点7、节点8是树的末端，没有子节点，被称为叶子节点（leaf）；
• 子树：以一个节点的子节点为根节点形成的就树称为该节点的子树，图中虚线部分，是根节点1的其中一个子树；

有关树的度和层次（如下图）

• 节点的度 ：对于一个结点，拥有的子树个数（结点有多少分支）称为结点的度（Degree）；例如，根结点 A 下分出了 3 个子树，所以，结点 A 的度为 3。

• 树的度：一棵树的度是树内各节点的度的最大值；例如，所有结点的度的最大值为 3，所以，整棵树的度的值是 3。
• 节点层次：从一棵树的树根开始，树根所在层为第一层，根的子结点所在的层为第二层，依次类推；例如：A 结点在第一层，B、C、D 为第二层，E、F、G、H、I、J 在第三层，K、L、M 在第四层。
• 树的高度 ：一棵树的高度是树中结点所在的最大层次，也就是这棵树的叶子节点所在的层数。树的高度，也被称为树的深度；例如：树的高度为 4。

• 节点深度 ：根节点到该节点的路径所包含的边数；例如：节点A是根节点，深度为0，子节点E与根节点A之间的路径包含边数为2，所以子节点E深度为2。

• 节点高度：该节点到叶子节点的最长路径所包含的边数；例如：节点B到叶子节点K之间的路径包含边数为2，所以节点B高度为2。

树的特点

在任意一个非空树中，有如下特点：

1. 有且仅有一个根节点；
2. 一棵树中的任意两个结点，有且仅有唯一的一条路径连通，不包含回路；
3. 一棵树如果有 n 个结点，那么它一定有 n-1 条边；

Binary Tree 二叉树

• 二叉树（Binary Tree）是一种特殊的有序树。

• 每个节点最多只有两个子节点：树中包含的各个节点的度不能超过 2，即只能是 0、1 或者 2。如下图，a是二叉树，b不是二叉树，因为b的根节点的度是3。

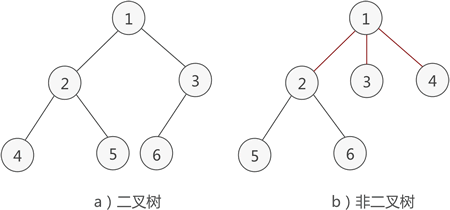
• 子节点通常被称作“左孩子节点”或“右孩子节点”，子节点的左右次序不能颠倒，左孩子节点小于父节点，右孩子节点大于父节点。所以，二叉树是有序树。如上图，二叉树a中节点2是根节点1的左孩子节点，节点3是根节点1的右孩子节点。

二叉树的分类

二叉树被分为满二叉树和完全二叉树。

满二叉树

如果二叉树中除了叶子结点，每个结点的度都为 2，也可以理解为：一个二叉树的所有非叶子节点都存在左右子节点，并且所有叶子节点都在同一层级上。满足上述条件的二叉树称为满二叉树。

满二叉树除了满足普通二叉树的性质，还具有以下性质：

• 一个层数为k的满二叉树，总节点数 = -1,如上图所示，该满二叉树的层数为3，所以总节点数为；
• 第i层的节点数 = ，如上图所示，该满二叉树的第3层有个节点；
• 一个层数为k的满二叉树，叶子节点数 = ，如上图所示，该满二叉树的层数为3，所以它的叶子节点为；
• 具有x个节点的满二叉树，叶子节点数 = (x+1)/2，如上图所示，该满二叉树的层数为3，所以总节点数为，因此，叶子节点数为(7+1)/2=4;
• 具有n个节点的满二叉树，深度为 log2(n+1),如上图所示，该满二叉树的层数为3，所以总节点数为，因此,深度为log2(7+1)=3;

完全二叉树

如果二叉树中除去最后一层节点为满二叉树，且最后一层的结点依次从左到右分布，则此二叉树被称为完全二叉树。

完全二叉树有一个很好的性质：父结点和子节点的序号有对应关系。

例如：当根节点的序号值为 1 的情况下，若父结点的序号是 i，那么左子节点的序号就是 2i，右子节点的序号是 2i+1。这个性质使得完全二叉树利用数组存储时可以极大地节省空间，以及利用序号找到某个节点的父结点和子节点。

二叉树的存储

二叉树的存储方式主要分为 链式存储 和 顺序存储 两种：

链式存储

和链表类似，二叉树的链式存储依靠指针将各个节点串联起来，不需要连续的存储空间。

每个节点包括3个属性：

• • 数据 Data
  • 左孩子节点指针 Left
  • 右孩子节点指针 Right

顺序存储

二叉树的顺序存储，指的是使用顺序表（数组）存储二叉树。需要注意的是，顺序存储只适用于完全二叉树。满二叉树也是完全二叉树，所以同样适用。

在顺序存储中，顺序表（数组）中的每一个位置仅存储节点的 data，不需要存储左右子节点的指针，子节点的索引通过计算父节点下标完成。

• 假设一个父节点的下标是parentIndex，它的左子节点下标 = 2×parentIndex；右子节点下标 = 2×parentIndex + 1
• 假设一个左子节点的下标是leftChildIndex，它的父节点 下标= leftChildIndex/ 2
• 假设一个右子节点的下标是rightChildIndex，它的父节点 下标= (rightChildIndex-1)/ 2

一棵完全二叉树的数组顺序存储如下图所示：

具体的的代码实现如下：

package com.hpc.demo01;

import javax.swing.tree.TreeNode;

public class BinaryTree<E> {
	private Object[] elementDatas=null;
	
	public BinaryTree(E[] elements){
		elementDatas=new Object[elements.length+1];
		for(int i=0;i<elements.length;i++) {
			elementDatas[i+1]=elements[i];
		}
	}
	
	public E get(int index) {
		return (E) elementDatas[index];
	}
	
	public E left(int index) throws Exception {
		if((index<<1)>=elementDatas.length) {
			throw new Exception("左孩子节点不存在！");
		}
		return (E) elementDatas[index<<1];
	}
	
	
	public E right(int index) throws Exception {
		if((index<<1)+1>=elementDatas.length) {
			throw new Exception("右孩子节点不存在！");
		}
		return (E) elementDatas[(index<<1)+1];
	}
}

 测试类如下：

package com.hpc.demo01;

public class Test01 {
	public static void main(String[] args) throws Exception {
		BinaryTree<String> tree=new BinaryTree<String>(new String[] {"A","B","C","D","E","F","G","H"});
		
		System.out.println(tree.get(4));
		System.out.println(tree.left(4));
		System.out.println(tree.right(4));
	}

}

 测试结果如下：

D
H
Exception in thread "main" java.lang.Exception: 右孩子节点不存在！
	at com.hpc.demo01.BinaryTree.right(BinaryTree.java:29)
	at com.hpc.demo01.Test01.main(Test01.java:9)

由上述测试结果可知，我们可以根据下标去获取某个节点的父节点和左孩子节点或右孩子节点，如上图，下标为4的节点D只有左孩子节点，没有右孩子节点，因此，抛出异常：右孩子节点不存在！ 

如果普通二叉树使用顺序存储，在数组中就会出现空隙，导致内存利用率降低

二叉树的遍历

• 前序遍历：根节点->左子树->右子树（根->左->右）
• 中序遍历：左子树->根节点->右子树（左->根->右）
• 后序遍历：左子树->右子树->根节点（左->右->根）

前序遍历： ABDECFG

中序遍历：DBEAFCG

后序遍历：DEBFGCA