学习笔记-针孔/鱼眼模型相机畸变

(搬运了很多博主写的文章，如有侵权立删并表示抱歉！)

鱼眼镜头的成像原理到畸变矫正（完整版）_鱼眼畸变-优快云博客

1.针孔相机畸变模型

1.1 径向畸变

在相机制造过程中，很难保证镜头的厚度完全均匀，由于制造工艺的原因，通常这种情况为中间厚、边缘薄，因而光线在远离透镜中心的地方，会发生更大程序的扭曲。径向畸变是沿着透镜半径方向分布的畸变，光线在原理透镜中心的地方比靠近中心的地方更加弯曲，光线离主轴越远，畸变越大。包括枕形畸变和桶形畸变。

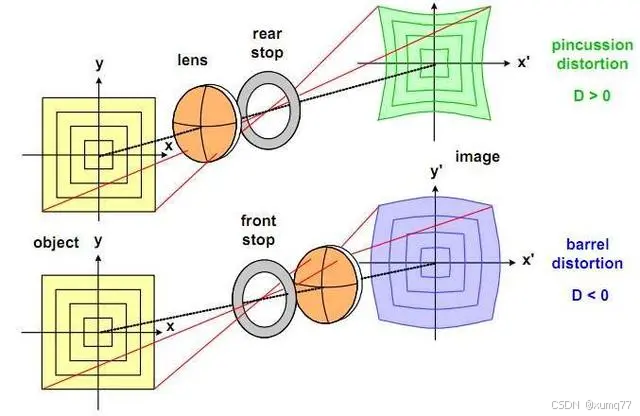包括

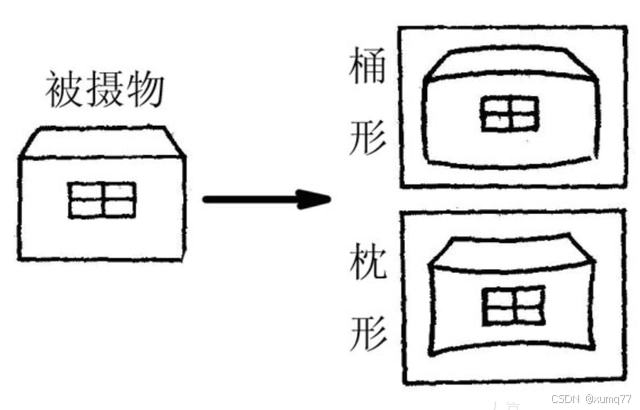
广角镜头变形效果是桶形畸变，长焦镜头变形效果是枕形畸变。

实际情况中我们常用 r = 0处的泰勒级数展开的前几项来近似描述径向畸变。

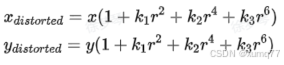
下图表示是光心不同距离的点经过透镜径向畸变后的便宜示意图，距离光心越远，径向畸变唯一越大，在光心附件几乎没有偏移。

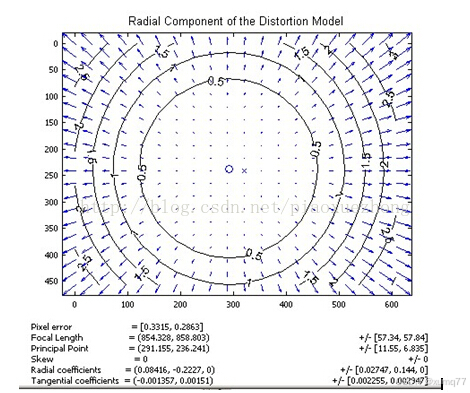
通常只用k1、k2来矫正相机，k1对于畸变较小的图像中心区域有很大的作用和影响；
对于畸变较大的图像边缘区域，主要是k2在起作用，k3一般用于广角相机，鱼眼相机。

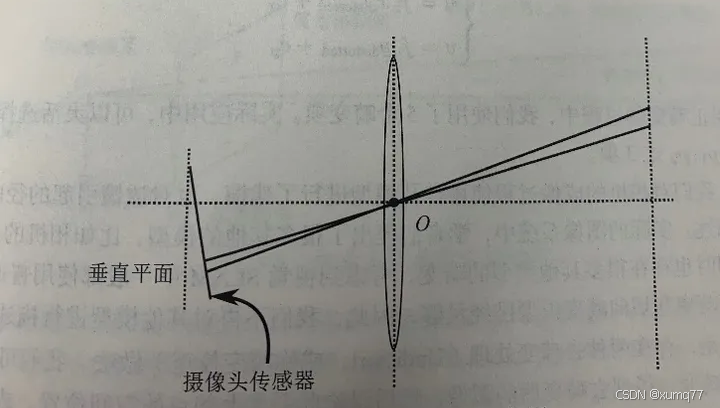
1.2 切向畸变

在相机制造过程中，成像平面与透镜平面不平行，产生切向畸变。

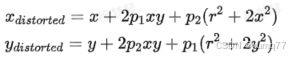
1.3 总畸变模型

综上，

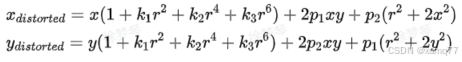
一般用K1,K2,K3,P1,P2五个参数来描述针孔模型的畸变。

2.鱼眼相机畸变模型

2.1 Kannala-Brandt模型

鱼眼相机所成影像存在畸变，其中径向畸变非常严重，因此其畸变模型主要考虑径向畸变。鱼眼镜头生产过程中不可能精确地按照投影模型来设计，所以为了方便鱼眼相机的标定，Kannala-Brandt提出了一种鱼眼相机的一般多项式近似模型。是入射角θ的奇函数，将这些式子按泰勒级数展开，发现θd用θ的奇次多项式表示。

鱼眼相机的畸变系数是k0，k1，k2，k3，k4.

，由于f不影响畸变模型，那么

那么

由相似关系可得

2.2 投影过程

另一种解法：

2.3 投影过程