2024年CSP-S组（提高组）试题+答案

最新推荐文章于 2025-11-10 14:11:03 发布

原创最新推荐文章于 2025-11-10 14:11:03 发布 · 2.8k 阅读

19 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构 #CSP-J/S #c++

CSP-J/S 专栏收录该内容

5 篇文章

订阅专栏

1. 在 Linux 系统中，如果你想显示当前工作目录的路径，应该使用哪个命令？（）

A. pwd B. cd C. Ls D. echo

2. 假设一个长度为 n 的整数数组中每个元素互不相同，且这个数组是无序的。要找到这个数组中最大元素的时间复杂度是多少？（）

A. O(n) B. O(log n) C. O(n log n) D. O(1)

3. 在 C++中，以下哪个函数调用会造成栈溢出？（）

A. int foo( return 0; )

B. Int bar( int x=1; return x)

C. Void baz(){int a[1000]; baz();}

D. Void qux(){return;}

4. 在一场比赛中，有 10 名选手参加，前三名将获得金银铜牌，若不允许并列，且每名选手只能获得一枚铜牌，则不同的颁奖方式共有多少种？（）

A.120 B.720 C.504 D.1000

5. 下面那个数据结构最适合实现先进先出（FIFO）的功能？（）

A. 栈 B. 队列 C. 线性表 D. 二叉搜索树

6. 一直 f(1) = 1,且对于 n>=2 有 f(n) = f(n − 1) + f( n/2 ) ,则 f(4)的值为：（）

A.4 B.5 C.6 D.7

7. 假设一个包含 n 个顶点的无向图，且该图是欧拉图。一下关于该图的描述中哪一项不一定正确？（）

A. 所有顶点的度数均为偶数 B. 该图联通 C. 该图存在一个欧拉回路 D. 该图的边数是奇数

8. 对数组进行二分查找的过程中，以下哪个条件必须满足？（）

A.数组必须是有序的

B.数组必须是无序的

C.数组长度必须是 2 的幂

D.数组中的元素必须是整数

9. 考虑一个自然数 n 以及一个模数 m，你需要计算 n 的逆元（即 n 在模 m 意义下的乘法逆元）。下列哪种算法最为合适？（）

A. 使用暴力方法依次尝试

B. 使用扩展欧几里得解法

C. 使用快速幂解法

D. 使用线性筛法

10. 在设计一个哈希表时，为了减少冲突，需要使用适当的哈希函数和和冲突解决策略。已知某哈希表中有 n 个键值对，表的装载因子为α（0α）。在使用开放地址法解决冲突的过程中，最坏情况下查找一个元素的时间复杂度为（）

A. O(1) B. O(log n) C. O (1/(1-α)) D. O(n)

11. 假设有一颗 h 层的完全二叉树，该树最多包含多少个节点（）

A. 2^ℎ − 1 B. 2^(ℎ+1) − 1 C. 2^ℎ D. 2^(ℎ+1)

12. 设有一个 10 个顶点的完全图，每两个顶点之间都有一条边，有多少个长度为 4 的环？（）

A.120 B.210 C.630 D.5040

13. 对于一个整数 n，定义 f(n)为 n 的各个位数之和，问使 f(f(x))=10 的最小自然数 x 是多少?（）

A.29 B.199 C.299 D.399

14. 设有一个长度为 n 的 01 字符串，其中有 k 个 1，每次操作可以交换相邻两个字符。在最坏的情况下将这 k 个 1 移到字符串最右边所需要的交换次数是多少？（）

A. K B. K*(k-1)/2 C. (n-k)*k D. (2n-k-1)*k/2

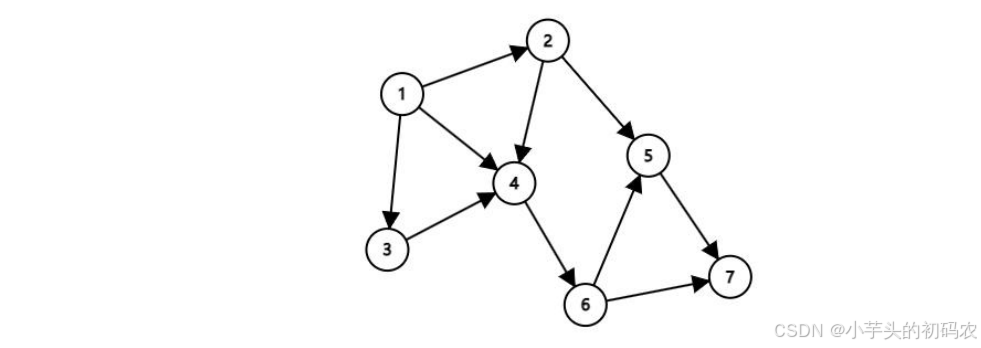
15. 如图是一张包含 7 个顶点的有向图。如果要删除一些边，使得从节点 1 到节点 7 没有可行路径，且删除的边数最少，请问总共有多少种可行的删除边的集合？（）

A.1 B.2 C.3 D.4

二、阅读程序

（程序输入不超过数组或字符串定义的范围；判断题正确填√，错误填×，除特殊说明外，判断题 1.5 分，选择题 3 分，共计 40 分）

（1）

1 #include <iostream>
2 using namespace std;
3
4 const int N = 1000;
5 int c[N];
6
7 int logic(int x, int y) {
8 return (x & y) ^ ((x ^ y) | (~x & y));
9 }
10 void generate(int a, int b, int *c) {
11 for (int i = 0; i < b; i++) {
12     c[i] = logic(a, i) % (b + 1);
13 }
14 }
15 void recursion(int depth, int *arr, int size) {
16 if (depth <= 0 || size <= 1)return;
17 int pivot = arr[0];
18 int i = 0, j = size - 1;
19 while (i <= j) {
20     while (arr[i] < pivot)i++;
21     while (arr[j] > pivot)j--;
22     if (i <= j) {
23         int temp = arr[i];
24         arr[i] = arr[j];
25         arr[j] = temp;
26         i++;j--;
27     }
28 }
29 recursion(depth - 1, arr, j + 1);
30 recursion(depth - 1, arr + i, size - i);
31 }
32
33 int main() {
34 int a, b, d;
35 cin >> a >> b >> d;
36 generate(a, b, c);
37 recursion(d, c, b);
38 for (int i = 0; i < b; i++)cout << c[i] << " ";
39 }

判断题：

16. 当 1000>=d>=b 时，输出的序列是有序的（ T ）

17. 当输入“5 5 1”时，输出为“1 1 5 5 5”（ F ）

18. 假设数组 c 长度无限制，该程序所实现的算法的时间复杂度是 O(b)的（ F ）

单选题：

19. 函数 int logic(int x,int y)的功能是（）

A. 按位与 B. 按位或 C. 按位异或 D. 以上都不是

20. （4 分）当输入为“10 100 100”时，输出的第 100 个数是（）

A.91 B.94 C.95 D.98

1 #include <iostream>
2 #include <string>
3 using namespace std;
4
5 const int P = 998244353, N = 1e4 + 10, M = 20;
6 int n, m;
7 string s;
8 int dp[1 << M];
9
10 int solve() {
11 dp[0] = 1;
12 for (int i = 0; i < n; i++) {
13     for (int j = (1 << (m - 1)) - 1; j >= 0; j--) {
14         int k = (j << 1) | (s[i] - '0');
15         if (j != 0 || s[i] == '1')
16             dp[k] = (dp[k] + dp[j]) % P;
17     }
18     }
19 int ans = 0;
20 for (int i = 0; i < (1 << m); i++) {
21     ans = (ans + 1ll * i * dp[i]) % P;
22 }
23 return ans;
24 }
25 int solve2() {
26 int ans = 0;
27 for (int i = 0; i < (1 << n); i++) {
28     int cnt = 0;
29     int num = 0;
30     for (int j = 0; j < n; j++) {
31         if (i & (1 << j)) {
32             num = num * 2 + (s[j] - '0');
33             cnt++;
34         }
35     }
36     if (cnt <= m)(ans += num) %= P;
37 }
38 return ans;
39 }
40
41 int main() {
42     cin >> n >> m;
43     cin >> s;
44     if (n <= 20) {
45         cout << solve2() << endl;
46     }
47     cout << solve() << endl;
48     return 0;
49 }

21. 假设输入的 s 是包含 n 个字符的 01 串，函数 solve()所实现的算法时间复杂度是 O(n*2^m)。（ T ）

22. 输入“11 2 10000000001”时，程序输出两个数 32 和 23.（ T ）

23. （2 分）在 n<10时，solve()的返回值始终小于4^(10)（ T ）

单选题

24. 当 n=10 且 m=10 时，有多少种输入使得两行的结果完全一致？（）

A.1024 B.11 C.10 D.0

25. 当 n时，solve()的最大可能返回值为？（）

A.65 B.211 C.665 D.2059

26. 若 n=8，m=8，solve 和 solve2 的返回值的最大可能的差值为（）

A.1477 B.1995 C.2059 D.2187

(3)

1 #include <iostream>
2 #include <cstring>
3 #include <algorithm>
4 using namespace std;
5
6 const int maxn = 1000000 + 5;
7 const int P1 = 998244353, P2 = 1000000007;
8 const int B1 = 2, B2 = 31;
9 const int K1 = 0, K2 = 13;
10
11 typedef long long ll;
12
13 int n;
14 bool p[maxn];
15 int p1[maxn], p2[maxn];
16
17 struct H {
18     int h1, h2, l;
19     H(bool b = false) {
20         h1 = b + K1;
21         h2 = b + K2;
22         l = 1;
23     }
24     H operator + (const H &h)const {
25         H hh;
26         hh.l = l + h.l;
27         hh.h1 = (1ll * h1 * p1[h.l] + h.h1) % P1;
28         hh.h2 = (1ll * h2 * p2[h.l] + h.h2) % P2;
29         return hh;
30     }
31     bool operator == (const H &h)const {
32         return l == h.l && h1 == h.h1 && h2 == h.h2;
33     }
34     bool operator < (const H &h)const {
35         if (l != h.l)return l < h.l;
36         else if (h1 != h.h1) 
                return h1 < h.h1;
37         else return h2 < h.h2;
38     }
39 } h[maxn];
40
41 void init() {
42     memset(p, 1, sizeof(p));
43     p[0] = p[1] = false;
44     p1[0] = p2[0] = 1;
45     for (int i = 1; i <= n; i++) {
46         p1[i] = (1ll * B1 * p1[i - 1]) % P1;
47         p2[i] = (1ll * B2 * p2[i - 1]) % P2;
48         if (!p[i])continue;
49         for (int j = 2 * i; j <= n; j += i) {
50             p[j] = false;
51         }
52     }
53 }
54
55 int solve() {
56     for (int i = n; i; i--) {
57         h[i] = H(p[i]);
58         if (2 * i + 1 <= n) {
59             h[i] = h[2 * i] + h[i] + h[2 * i + 1];
60         } else if (2 * i <= n) {
61             h[i] = h[2 * i] + h[i];
62         }
63     }
64     cout << h[1].h1 << endl;
65     sort(h + 1, h + n + 1);
66     int m = unique(h + 1, h + n + 1) - (h + 1);
67     return m;
68 }
69
70 int main() {
71     cin >> n;
72     init();
73     cout << solve() << endl;
74 }

判断题

27. 假设程序运行前能自动将 maxn改为 n+1，所实现的算法的时间复杂度是 O(nlogn)。( T )

28. 时间开销的瓶颈是 init()函数（ F ）

29. 若修改常数 B1 或 K1 的值，该程序可能会输出不同呢的结果（ T ）

单选题

30. 在 solve()函数种，h[]的合并顺序可以看作是：（）

A. 二叉树的 BFS 序

B. 二叉树的先序遍历

C. 二叉树的中序遍历

D. 二叉树的后序遍历

31. 输入“10”，输出的第一行是？（）

A.83 B.424 C.54 D.110101000

32. (4 分)输入“16”，输出的第二行是？（）

A.7 B.9 C.10 D.12

三．完善程序（单选题，每小题 3 分，共计 30 分）

（1）合并序列，有两个长度为 N 的单调不降序列 A 和 B，序列的每个元素都是小于 10^9 的非负整数。在 A 和 B 中各取一个数相加可以得到 N^2 个和，求其中第 k 小的和。上述参数满足 N和 N<=10^5和1<=K<=N^2

#include <iostream>
using namespace std;
const int maxn = 100005;
int n;
long long k;
int a[maxn], b[maxn];
int *upper_bound(int *a, int *an, int ai) {
    int l = 0, r = (1) ;
    while (l < r) {
        int mid = (l + r) >> 1;
        if ( (2) ) {
            r = mid;
        } else {
            l = mid + 1;
        }
    }
return (3) ;
long long get_rank(int sum) {
    long long rank = 0;
    for (int i = 0; i < n; i++) {
        rank += upper_bound(b, b + n, sum - a[i]) - b;
    }
    return rank;
}
int solve() {
    int l = 0, r = (4) ;
    while (l < r) {
        int mid = ((long long)l + r) >> 1;
        if ( (5) ) {
            l = mid + 1;
        } else {
            r = mid;
        }
    }
    return l;
}
int main() {
    cin >> n >> k;
    for (int i = 0; i < n; i++)
        cin >> a[i];
    for (int i = 0; i < n; i++)
        cin >> b[i];
    cout << solve() << endl;
    return 0;
}

33. （1）处应填（）

A.an-a B.an-a-1 C.ai D.ai+1

34. (2)处应填（）

A.a[mid]>ai

B.a[mid]>=ai

C.a[mid]<ai

D.a[mid]<=ai

35. (3)处应填（）

A.a+l B.a+l+1 C.a+l-1 D.an-l

36. (4)处应填（）

A.a[n-1]+b[n-1] B.a[n]+b[n] C.2*maxn D.maxn

37. (5)处应填（）

A.get_rank(mid)<k B.get_rank(mid)<=k C.get_rank(mid)>k D.get_rank(mid)>=k

(2) （次短路）已知有一个 n 个点 m 条边的有向图 G，并且给定图中的两个点 s 和 t，求次短路（长度严格大于最短路的最短路径）。如果不存在，输出一行“-1”。如果存在，输出两行，第一行表示此段路经的长度，第二行表示此段路的一个方案

#include <cstdio>
#include <queue>
#include <utility>
#include <cstring>
using namespace std;
const int maxn = 2e5 + 10, maxm = 1e6 + 10, inf = 522133279;
int n, m, s, t;
int head[maxn], nxt[maxm], to[maxm], w[maxm], tot = 1;
int dis[maxn << 1], *dis2;
int pre[maxn << 1], *pre2;
bool vis[maxn << 1];
void add(int a, int b, int c) {
    ++tot;
    nxt[tot] = head[a];
    to[tot] = b;
    w[tot] = c;
    head[a] = tot;
}
bool upd(int a, int b, int d, priority_queue<pair<int, int> > &q) {
    if (d >= dis[b])return false;
    if (b < n) (1) ;
    q.push( (2) );
    dis[b] = d;
    pre[b] = a;
    return true;
}
void solve() {
    priority_queue<pair<int, int> >q;
    q.push(make_pair(0, s));
    memset(dis, (3) , sizeof(dis));
    memset(pre, -1, sizeof(pre));
    dis2 = dis + n;
    pre2 = pre + n;
    dis[s] = 0;
    while (!q.empty()) {
        int aa = q.top().second;q.pop();
        if (vis[aa])continue;
        vis[aa] = true;
        int a = aa % n;
        for (int e = head[a]; e; e = nxt[e]) {
            int b = to[e], c = w[e];
            if (aa < n) {
                if (!upd(a, b, dis[a] + c, q))
                    (4)
            } else {
                upd(n + a, n + b, dis2[a] + c, q);
            }
        }
    }
}
void out(int a) {
    if (a != s) {
        if (a < n)
            out(pre[a]);
        else
            out( (5) );
    }
    printf("%d%c", a % n + 1, " \n"[a == n + t]);
}
int main() {
    scanf("%d%d%d%d", &n, &m,&s,&t);
    s--, t--;
    for (int i = 0; i < m; i++) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a - 1, b - 1, c);
    }
    solve();
    if (dis2[t] == inf)
        puts("-1");
    else {
        printf("%d\n", dis2[t]);
        out(n + t);
    }

38.(1)处应填（）

A.udp(pre[b],n+b,dis[b],q)

B.upd(a,n+b,d,q)

C.upd(pre[b],b,dis[b],q)

D.upd(a,b,d,q)

39.(2)处应填（）

A.make_pair(-d,b)

B.make_pair(d,b)

C.make_pair(b,d)

D.make_pair(-b,d)

40.(3)处应填（）

A.0xff B.0x1f C.0x3f D.0x7f