初识Numpy库总结自用

一、数组和列表的区别

创建数组：np.array([1，2，3，4])

创建列表：[1，2，3，4]

二、创建数组

1.直接创建数组

（1）创建1维数组：np.array( [ 1，2，3，4 ] ) 以列表为记忆点

（2）创建2维数组：np.array( [ [ ] , [ ] ] )，在一维的基础上再增加一维

2.快速创建数组

e=np.zeros((3,4)) 注意这里括号里面的数字指的是行列个数

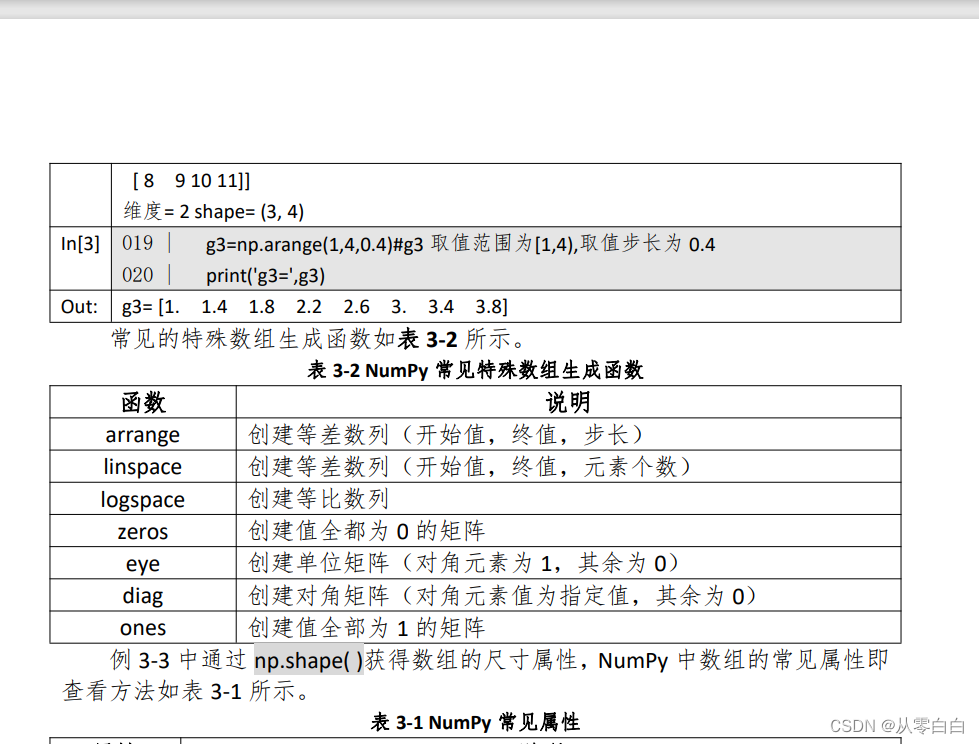
linspace区别在于左闭右闭。

3.创建随机数组：随机指的是伪随机，有众多seed，在某一个seed按顺序抽取

np.random.randn(3)

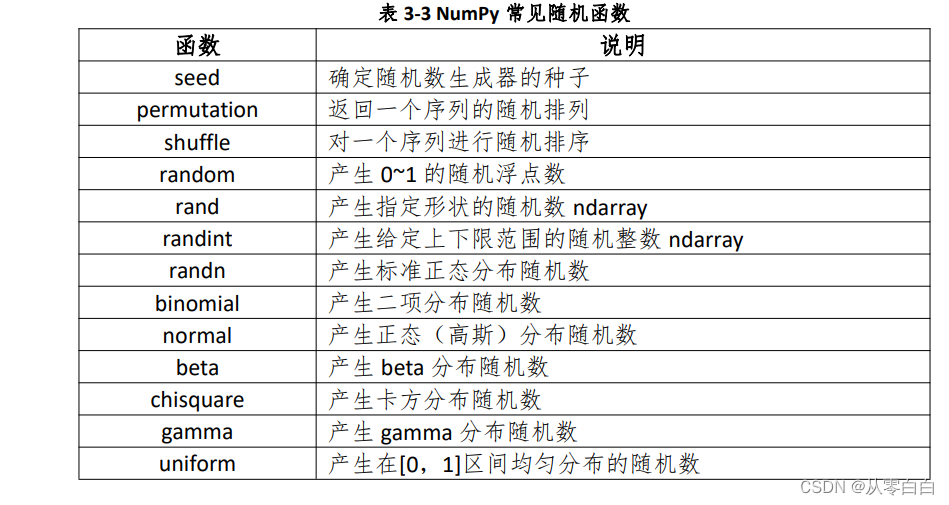
三、数组运算与访问元素

1.数组运算：加减乘除（两个数组元素个数相对应，行列必相等，任何元素都需要对判断条件进行判断）

类似列表会被处理

c+=a(先读＝再读+，c=c+a)

2.矩阵运算

np.dot(d,f),注意df顺序是不可以调换的，因为矩阵没有交换律

3.元素处理

以下是对矩阵中元素进行处理的函数列表，包括数学处理和统计处理

输出某一条件的元素，只需[]

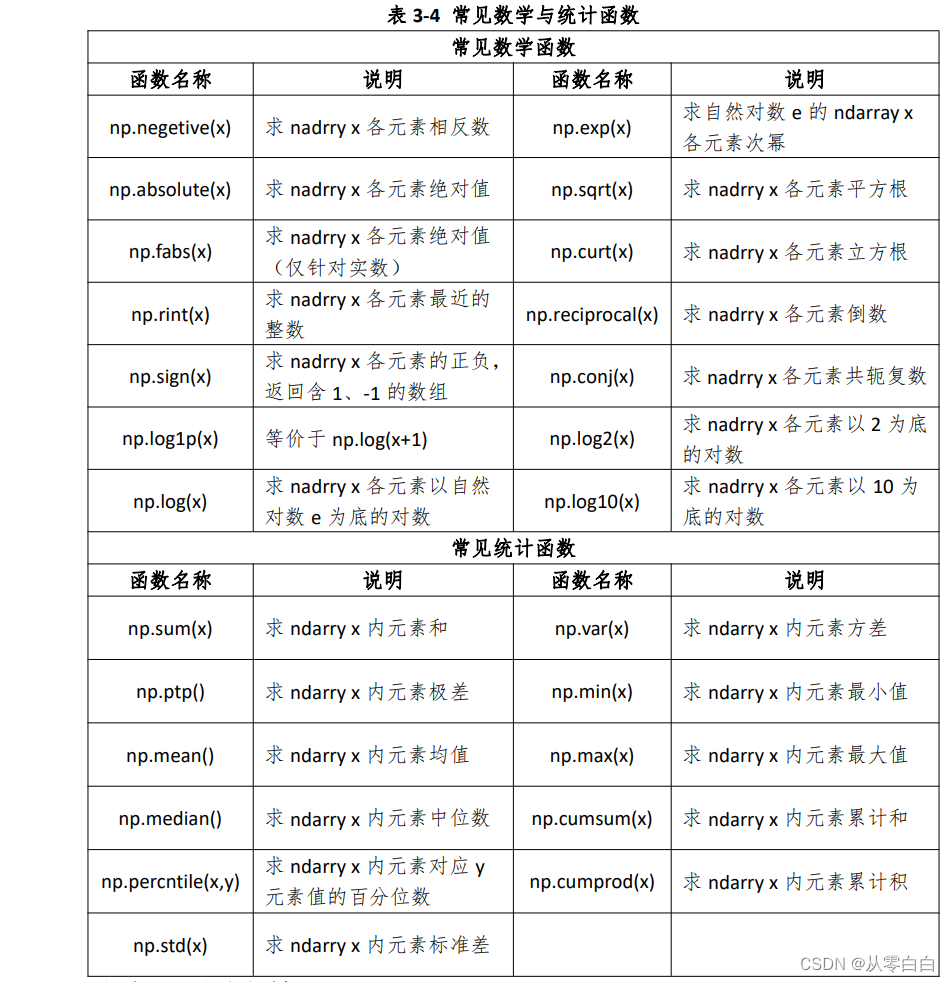
类似excel中的列求和，行求和，只需要规定axis值，=0列求和，=1行求和 

对数组中的元素进行排序np.sort(h),升序排序，降序思路可以为先相反数排序，再相反数则能够实现逆序

或者先顺序排列再倒着输出

输出特定条件的元素

print('对数组进行排序')
h=np.random.random(8)
print('随机数组',h,'\n','排序np.sort(h)后得到',np.sort(h)) #升序排列
h=-np.sort(-h)
print(h)
h2=np.sort(h)
h3=h2[::-1]
print(h3)





print('输出特定条件的元素')
k=np.array([[0,1,2],[3,4,5],[6,7,8],[9,10,11]])
print('数组k','\n',k,'\n','输出其中小于8的元素k[k<8]=',k[k<8])

三、数组运算与访问元素

1.数组运算

A.基本数学运算

加减乘除

注意c+=a:c=c+a

B.内置函数函数

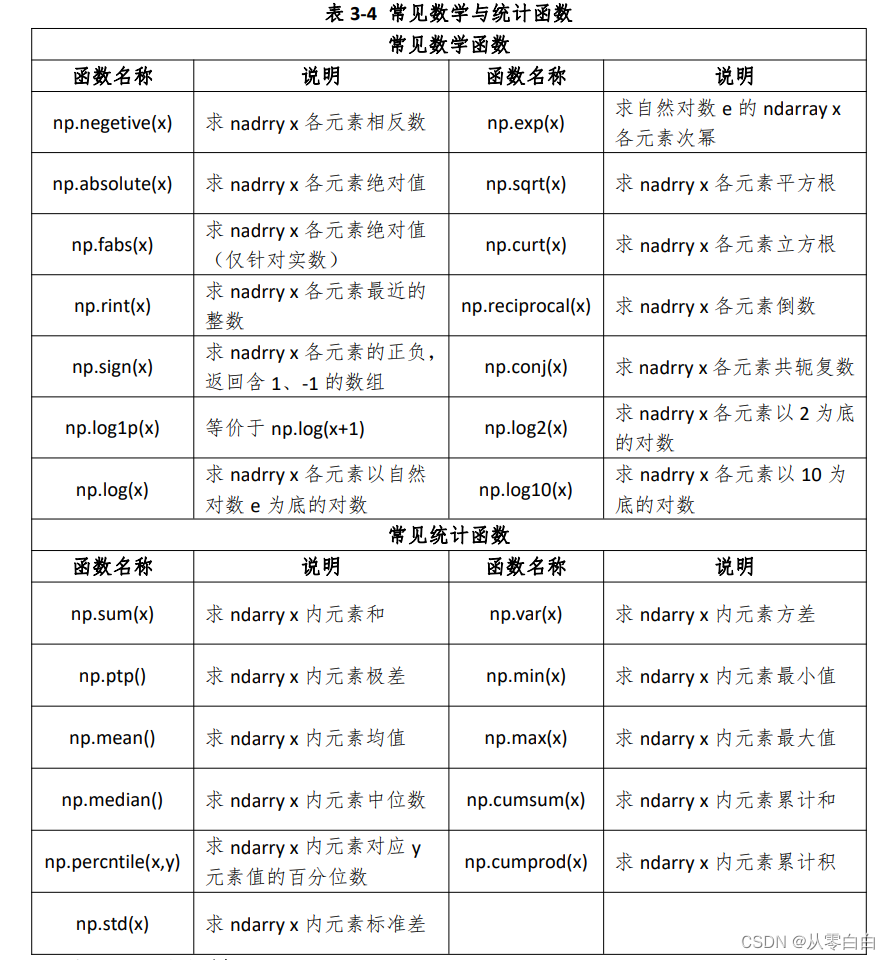
C.矩阵运算

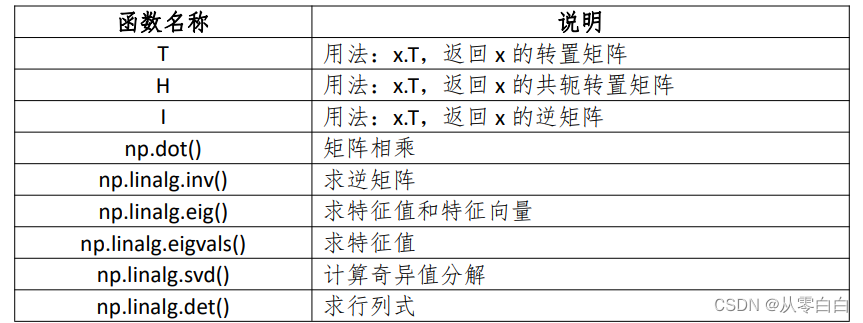
 2.访问元素

切片

索引

行列之间用逗号隔开

综合运用：

1.解线性方程

import numpy as np
import scipy.linalg as scig#必须引入scipy包用于求解线性方程
a=np.array([[3,1,-2],[1,-1,4],[2,0,3]])
b=np.array([5,-2,2.5])
print('方程形如ax=b,其中a=','\n',a,'\n','b=','\n',b)
print('方程的解为：',scig.solve(a,b))

2.利用numpy进行最小二乘参数估计

import numpy as np

#模拟样本数据
np.random.seed(123) #设定随机种子以便重现
x1 = np.random.normal(1, 2, 100)#随机生成解释变量x1
x2 = np.random.uniform(1, 2, 100)#随机生成解释变量x2
b = np.ones(100)         #产生100个1
X = np.array([b,x1,x2]).T   #产生样本解释变量矩阵X=[X1,X2,X3]
y = 2.5 + 2* x1 - 3* x2 + np.random.normal(0, 1, 100)#产生样本被解释变量
print('样本解释变量矩阵前三行前三列为','\n',X[:3,:3])
print('样本被解释变量y的前10个值为',y[:10])

#进行参数估计，运用矩阵运算求解参数
b_hat = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)#运用式3-1计算参数估计值 
print('参数估计值为',b_hat)

#求得被解释变量拟合值与回归残差，用作后续检验
y_hat = X.dot(b_hat) #运用式3-2计算被解释变量拟合值
print('被解释变量拟合值前10个值为：',y_hat[:10])
res = y-y_hat#运用计算回归残差

import statsmodels.api as sm  #加载statsmodels程序包
import numpy as np

#模拟样本数据（同上）
np.random.seed(123) #设定随机种子以便重现
x1 = np.random.normal(1, 2, 100)#随机生成解释变量x1
x2 = np.random.uniform(1, 2, 100)#随机生成解释变量x2
b = np.ones(100)         #产生100个1
X = np.array([b,x1,x2]).T   #产生样本解释变量矩阵X=[X1,X2,X3]
y = 2.5 + 2* x1 - 3* x2 + np.random.normal(0, 1, 100)#产生样本被解释变量
print('样本解释变量矩阵前三行前三列为','\n',X[:3,:3])
print('样本被解释变量y的前10个值为',y[:10],'\n')
model = sm.OLS(y,X)         #产生普通最小二乘OLS模型对象
result = model.fit()                            #训练模型
print('回归结果为','\n',result.summary())       #回归结果汇总