逻辑回归算法相关数学知识(极大似然估计及sigmoid函数)

1 极大似然估计

1.1 极大似然估计引入

例子：我与一位猎人一起外出打猎，一只野兔从前方穿过，只听到一声枪响，野兔应声倒下。问是谁打下的呢？

​ 答：极有可能是猎人。

​ 显然候选人就两个，我和猎人。若选择我，则事件发生的发生概率为0.01%，因为我不会打猎；若选择猎人，则事件发生的概率为99%，而事件已经发生，因此选择猎人更为合适。

​ 极大似然估计的思想

​设总体中含有待估参数w。已经观测样本数据（对于机器学习来讲,就是样本），从观测样本中选择出现概率最大的作为w参数的估计值，这就是极大似然估计。（顾名思义：就是看上去那个是最大可能的意思）
**核心:**根据观测到的结果来估计模型算法中的未知数

1.2 极大似然估计步骤

求极大似然函数估计值的一般步骤：

（1） 写出似然函数；

（2） 对似然函数取对数，并整理；(化简)

（3） 求导数 ；

（4） 解似然方程

极大似然估计，只是一种概率论在统计学的应用，它是参数估计的方法之一。说的是**已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察其结果，利用结果推出参数的大概值。**极大似然估计是建立在这样的思想上：已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。
　　当然极大似然估计只是一种粗略的数学期望，要知道它的误差大小还要做区间估计。

1.3 极大似然估计示例

1.3.1 示例1

1.3.2 示例2

1.3.3 示例3

2 Sigmoid函数

2.1 逻辑斯特函数的由来

Sigmod函数，也称之为逻辑斯特函数

假设一事件发生的概率为P，则不发生的概率为1-P，我们把发生概率/不发生概率称之为发生的概率比，数学公式表示为：

更进一步我们定义logit函数，它是概率比的对数函数（log-odds）

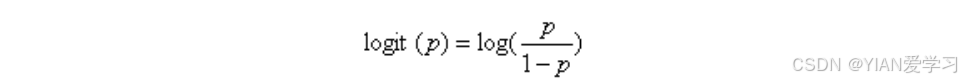
Logit函数耳朵输入值范围介于[0,1]之间，它能将输入转换到整个实数范围内。

对logit函数求反函数，我们将logit的反函数叫做logistic函数：

该函数的图像如下图：

对图像的理解：sidmod函数以实数值作为输入并将其反射到[0，1]区间，拐点在y=0.5地方。

2.2 Sigmod函数绘图

• 需求：绘制[-7，7]的sigmod函数图像

import matplotlib.pyplot as plt
import numpy as np
def sigmod(z):
    return 1.0/(1.0+np.exp(-z))
z=np.arange(-7,7,0.1)
phi_z=sigmod(z)
plt.plot(z,phi_z)
plt.axvline(0.0,color='k')
plt.axhspan(0.0,1.0,facecolor='1.0',alpha=1.0,ls='dotted')
plt.yticks([0.0,0.5,1.0])
plt.ylim(-0.1,1.1)
plt.xlabel('z')
plt.ylabel('$\phi (z)$')
plt.show()

1. 逻辑回归的分类结果是通过属于某个类别的概率值来判断
2. 预测概率大于 50% 则分为类1类别(正例), 反之为0类别(反例)

2.3 Sigmoid函数的使用

输出结果解释(重要)：假设有两个类别A，B，并且假设我们的概率值为属于A(1)这个类别的概率值。现在有一个样本的输入到逻辑回归输出结果0.55，那么这个概率值超过0.5，意味着我们训练或者预测的结果就是A(1)类别。那么反之，如果得出结果为0.3那么，训练或者预测结果就为B(0)类别。
关于逻辑回归的阈值是可以进行改变的，比如上面举例中，如果你把阈值设置为0.6，那么输出的结果0.55，就属于B类。