凸优化关于线性代数的复习

一.矩阵的表达

R m×n：表示一个m行n列的矩阵，矩阵的取值为实数

R n：n行的向量

二.矩阵乘法

x T y = y T x

每一列都相同的矩阵A可以表示为A=x 乘1 T（x为A的列向量，1T为转置1矩阵）

矩阵（矩阵乘向量，矩阵乘矩阵）乘法可以看作：

1.

2.

y is a linear combination of the columns of A

左乘表示行变换，右乘表示列变换

3.

 4.

对左边矩阵的列变换

5.

对右边矩阵的行变换

 三.矩阵的性质

满足结合律，分配律，但不满足交换律

-------------------------------

矩阵转置运算

关于矩阵的对称：

意味着A是一个对称矩阵

关于矩阵的迹的性质：

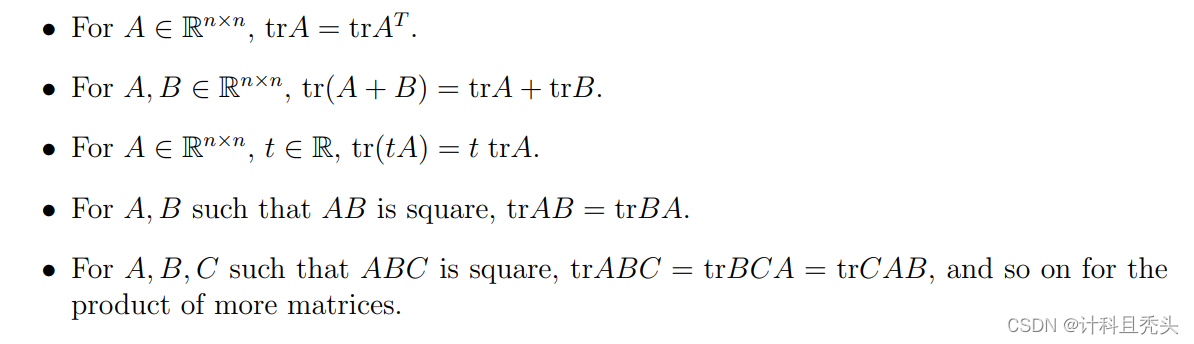
矩阵的模(norm)：

模运算的函数：

四.线性独立和秩

矩阵秩的性质：

矩阵的逆：

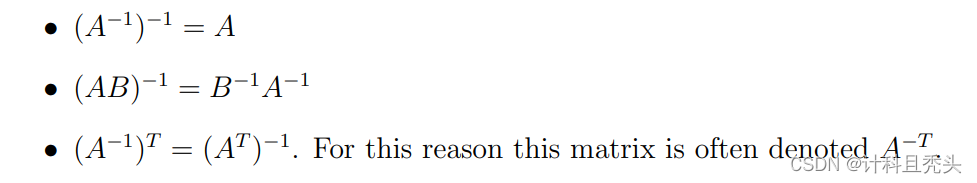
矩阵正交：

A square matrix U ∈ Rn×n is orthogonal (note the different meanings when
talking about vectors versus matrices) if all its columns are orthogonal to each other and are
normalized (the columns are then referred to as being orthonormal).

正交矩阵的转置乘他自身是单位矩阵

正交矩阵的逆就是他的转置

同时乘正交矩阵不会改变原矩阵的模

矩阵的列空间和零空间：

 矩阵的列空间和零空间是正交补的：

即：矩阵列空间的转置和零空间正交

关于矩阵的行列式（略）

二次型与正定、半正定矩阵：

常常隐式的假定二次型的矩阵是对称的；

关于正定、半正定等的符号定义：

一类矩阵需要特别注意：

对于任意A ∈ Rm×n，G = AT A总是半正定的，如果m >= n，则G是正定的 

注意特征向量和特征值的定义

特征值的性质：

 

任意一个满秩的正方形矩阵可以被对角化

 Λ为对角矩阵，对角线元素为A的特征值；U为彼此正交的单位特征向量组成的矩阵

后续还有一部分内容，不方便书写就不记录了