continue的用法示例（c++）——A、B、C的全排列

continue的用法示例（c++）——A、B、C的全排列

continue的作用：
跳出当前循环周期，回到循环控制行

#include <iostream>
using namespace std;

int main()
{
	char ch1, ch2, ch3;
	for (ch1 = 'A'; ch1 <= 'C'; ++ch1)     //第一个位置的值
		for (ch2 = 'A'; ch2 <= 'C'; ++ch2)//第二个位置的值
			if (ch1 == ch2) continue;    //第一个位置与第二个位置不能相同
			else for (ch3 = 'A'; ch3 <= 'C'; ++ch3)   //第三个位置的值
				if (ch3 == ch1 || ch3 == ch2) continue;//第三个位置和第一个第二个位置不能相同
				else cout << ch1 << ch2 << ch3 << endl;//输出
	return 0;
}

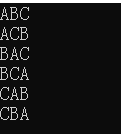
运行结果：