Leetcode 第284场周赛 总结
1. 找出数组中的所有 K 近邻下标
描述:
给你一个下标从 0 开始的整数数组 nums 和两个整数 key 和 k 。K 近邻下标 是 nums 中的一个下标 i ,并满足至少存在一个下标 j 使得 |i - j| <= k 且 nums[j] == key 。以列表形式返回按 递增顺序 排序的所有 K 近邻下标。
示例 1:
输入:nums = [3,4,9,1,3,9,5], key = 9, k = 1
输出:[1,2,3,4,5,6]
解释:因此,nums[2] == key 且 nums[5] == key 。
- 对下标 0 ,|0 - 2| > k 且 |0 - 5| > k ,所以不存在 j 使得 |0 - j| <= k 且 nums[j] == key 。所以 0 不是一个 K 近邻下标。
- 对下标 1 ,|1 - 2| <= k 且 nums[2] == key ,所以 1 是一个 K 近邻下标。
- 对下标 2 ,|2 - 2| <= k 且 nums[2] == key ,所以 2 是一个 K 近邻下标。
- 对下标 3 ,|3 - 2| <= k 且 nums[2] == key ,所以 3 是一个 K 近邻下标。
- 对下标 4 ,|4 - 5| <= k 且 nums[5] == key ,所以 4 是一个 K 近邻下标。
- 对下标 5 ,|5 - 5| <= k 且 nums[5] == key ,所以 5 是一个 K 近邻下标。
- 对下标 6 ,|6 - 5| <= k 且 nums[5] == key ,所以 6 是一个 K 近邻下标。
因此,按递增顺序返回 [1,2,3,4,5,6] 。
示例 2:
输入:nums = [2,2,2,2,2], key = 2, k = 2
输出:[0,1,2,3,4]
解释:对 nums 的所有下标 i ,总存在某个下标 j 使得 |i - j| <= k 且 nums[j] == key ,所以每个下标都是一个 K 近邻下标。
因此,返回 [0,1,2,3,4] 。
提示:
1 <= nums.length <= 10001 <= nums[i] <= 1000key是数组nums中的一个整数1 <= k <= nums.length
// 本人解法 核心思想:找到数组中的所有值为key的元素,并存储其下标。再通过每个下标找到k临近点
// 主要缺陷:代码能力不好,写的有些繁琐。对java的内置函数不熟悉
class Solution {
public List<Integer> findKDistantIndices(int[] nums, int key, int k) {
int n = nums.length;
List<Integer> ans = new ArrayList<>();
// 用于存储值为key的下标
List<Integer> find = new ArrayList<>();
for (int i = 0; i < n; i++) {
if (nums[i] == key) find.add(i);
}
// flag[i] == true 表示 已经存到答案里,不需要再次存储了;
boolean[] flag = new boolean[n];
// 依次遍历每个满足的下标,存储其k近邻点。
for (int j = 0; j < find.size(); j++) {
int index = find.get(j);
// 这里需要考虑越界情况!!
int w = index - k >= 0 ? index - k : 0;
for (int m = w ; m < n && m <= index + k; m++) {
if (!flag[m]) {
ans.add(m);
flag[m] = true;
}
}
}
return ans;
}
}
// 大神解法 @arignote (https://leetcode-cn.com/u/arignote/)
class Solution {
public List<Integer> findKDistantIndices(int[] nums, int key, int k) {
// 使用TreeSet存储 值为key的索引
TreeSet<Integer> set = new TreeSet<>();
for (int i = 0; i < nums.length; i++) {
if (nums[i] == key) {
set.add(i);
}
}
ArrayList<Integer> list = new ArrayList<>();
// 遍历每个 下标,判断是否满足 k近邻
for (int i = 0; i < nums.length; i++) {
// floor(E e)方法返回在这个集合中 <= e 的最大元素,如果不存在这样的元素,返回null.
if (set.floor(i + k) != null && set.floor(i + k) >= i - k) {
list.add(i);
}
}
return list;
}
}
总结: 内置函数/内置方法,多熟悉
2. 统计可以提取的工件
描述:
存在一个 n x n 大小、下标从 0 开始的网格,网格中埋着一些工件。给你一个整数 n 和一个下标从 0 开始的二维整数数组 artifacts ,artifacts 描述了矩形工件的位置,其中 artifacts[i] = [r1i, c1i, r2i, c2i] 表示第 i 个工件在子网格中的填埋情况:
(r1i, c1i)是第i个工件 左上 单元格的坐标,且(r2i, c2i)是第i个工件 右下 单元格的坐标。
你将会挖掘网格中的一些单元格,并清除其中的填埋物。如果单元格中埋着工件的一部分,那么该工件这一部分将会裸露出来。如果一个工件的所有部分都都裸露出来,你就可以提取该工件。
给你一个下标从 0 开始的二维整数数组 dig ,其中 dig[i] = [ri, ci] 表示你将会挖掘单元格 (ri, ci) ,返回你可以提取的工件数目。
生成的测试用例满足:
- 不存在重叠的两个工件。
- 每个工件最多只覆盖
4个单元格。 dig中的元素互不相同。
示例 1:
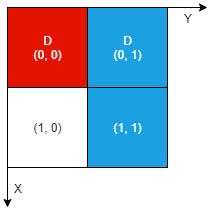
输入:n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1]]
输出:1
解释:
不同颜色表示不同的工件。挖掘的单元格用 'D' 在网格中进行标记。
有 1 个工件可以提取,即红色工件。
蓝色工件在单元格 (1,1) 的部分尚未裸露出来,所以无法提取该工件。
因此,返回 1 。
示例 2:
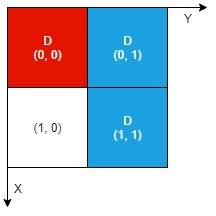
输入:n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1],[1,1]]
输出:2
解释:红色工件和蓝色工件的所有部分都裸露出来(用 'D' 标记),都可以提取。因此,返回 2 。
提示:
1 <= n <= 10001 <= artifacts.length, dig.length <= min(n2, 105)artifacts[i].length == 4dig[i].length == 20 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1r1i <= r2ic1i <= c2i- 不存在重叠的两个工件
- 每个工件 最多 只覆盖
4个单元格 dig中的元素互不相同
/* 本人解法: 1) 根据artifacts建好每个工件区域,并统计不同工件所占单元格数量
2) 根据dig遍历每个单元格,如果当前单元格存在工件,将其工件所占单元格数量-1;
3) 统计所有工件数量为0的个数
*/
class Solution {
public int digArtifacts(int n, int[][] artifacts, int[][] dig) {
// map存储每个工件所占的单元格数量
Map<Integer, Integer> map = new HashMap<>();
// 根据artifacts建好每个工件区域 不同工件用不同的index 标记
int[][] area = new int[n][n];
int index = 1;
for (int[] goods : artifacts) {
int cnt = 0;
int r1 = goods[0], c1 = goods[1];
int r2 = goods[2], c2 = goods[3];
for (int i = r1;i < n && i <= r2; i++) {
for (int j = c1; j < n && j <= c2; j++) {
area[i][j] = index;
cnt++;
}
}
map.put(index, cnt);
index++;
}
// 根据dig遍历每个单元格,如果当前单元格存在工件,将其工件所占单元格数量-1;
for (int[] find : dig) {
int r = find[0], c = find[1];
// area[r][c] != 0 说明有工件
if (area[r][c] != 0) {
// 工件标号
int value = area[r][c];
// 将其数量-1;
map.put(value, map.get(value) - 1);
}
}
// 统计其数量为0 的工件数
int ans = 0;
for (int k : map.keySet()) {
if (map.get(k) == 0) ans++;
}
return ans;
}
}
// 大神解法 @arignote (https://leetcode-cn.com/u/arignote/)
class Solution {
public int digArtifacts(int n, int[][] artifacts, int[][] dig) {
// 将dig转存到HashSet中
HashSet<List<Integer>> set = new HashSet<>();
for (int[] i : dig) {
set.add(List.of(i[0], i[1]));
}
// 遍历artifacts,统计挖掘工件数量
int count = 0;
for (int[] artifact : artifacts) {
// digArtifacts() 用于判断当前工件是否全被挖掘;是 1;否 0
count += digArtifacts(artifact, set);
}
return count;
}
private int digArtifacts(int[] artifact, HashSet<List<Integer>> set) {
// 遍历当前工件区域
for (int i = artifact[0]; i <= artifact[2]; i++) {
for (int j = artifact[1]; j <= artifact[3]; j++) {
// 只要有一个单元格在set中不存在,说明此工件未被(完全)挖掘
if (!set.contains(List.of(i, j))) {
return 0;
}
}
}
return 1;
}
}
总结: 无
3. K 次操作后最大化顶端元素
题目改过!!!!离谱!!!

描述:
给你一个下标从 0 开始的整数数组 nums ,它表示一个 栈 ,其中 nums[0] 是栈顶的元素。每一次操作中,你可以执行以下操作 之一 :
- 如果栈非空,那么 删除 栈顶端的元素。
- 如果存在 1 个或者多个被删除的元素,你可以从它们中选择任何一个,添加 回栈顶,这个元素成为新的栈顶元素。
同时给你一个整数 k ,它表示你总共需要执行操作的次数。请你返回 恰好 执行 k 次操作以后,栈顶元素的 最大值 。如果执行完 k 次操作以后,栈一定为空,请你返回 -1 。
示例 1:
输入:nums = [5,2,2,4,0,6], k = 4
输出:5
解释:
4 次操作后,栈顶元素为 5 的方法之一为:
- 第 1 次操作:删除栈顶元素 5 ,栈变为 [2,2,4,0,6] 。
- 第 2 次操作:删除栈顶元素 2 ,栈变为 [2,4,0,6] 。
- 第 3 次操作:删除栈顶元素 2 ,栈变为 [4,0,6] 。
- 第 4 次操作:将 5 添加回栈顶,栈变为 [5,4,0,6] 。
注意,这不是最后栈顶元素为 5 的唯一方式。但可以证明,4 次操作以后 5 是能得到的最大栈顶元素。
示例 2:
输入:nums = [2], k = 1
输出:-1
解释:
第 1 次操作中,我们唯一的选择是将栈顶元素弹出栈。
由于 1 次操作后无法得到一个非空的栈,所以我们返回 -1 。
提示:
1 <= nums.length <= 1050 <= nums[i], k <= 109
// 由于改前题目略坑,没做!血亏!!!!
// 大神解法 @arignote (https://leetcode-cn.com/u/arignote/)
class Solution {
public int maximumTop(int[] nums, int k) {
// 技巧点, 如果当前数组长度为1,只要执行奇数次操作,就一定会取完,所以返回-1;
if (nums.length == k % 2) {
return -1;
}
int max = 0;
// 找到前k-1个数的最大值 0 ~ k-2
for (int i = 0; i < Math.min(nums.length, k - 1); i++) {
max = Math.max(max, nums[i]);
}
// 第k次操作,要么添加已删除元素的最大值,要么就是删掉nums[k-1] 返回nums[k];
return Math.max(max, nums.length > k ? nums[k] : 0);
}
}
总结: 题目背锅我不背。
4. 得到要求路径的最小带权子图
描述:
给你一个整数 n ,它表示一个 带权有向 图的节点数,节点编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ,其中 edges[i] = [fromi, toi, weighti] ,表示从 fromi 到 toi 有一条边权为 weighti 的 有向 边。最后,给你三个 互不相同 的整数 src1 ,src2 和 dest ,表示图中三个不同的点。请你从图中选出一个 边权和最小 的子图,使得从 src1 和 src2 出发,在这个子图中,都 可以 到达 dest 。如果这样的子图不存在,请返回 -1 。
子图 中的点和边都应该属于原图的一部分。子图的边权和定义为它所包含的所有边的权值之和。
示例 1:
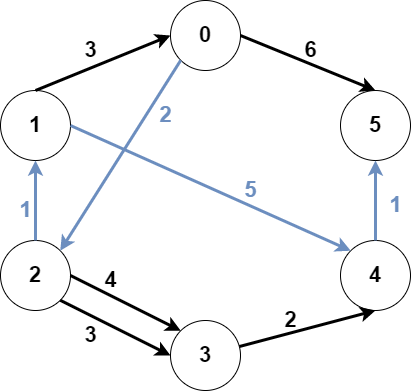
输入:n = 6, edges = [[0,2,2],[0,5,6],[1,0,3],[1,4,5],[2,1,1],[2,3,3],[2,3,4],[3,4,2],[4,5,1]], src1 = 0, src2 = 1, dest = 5
输出:9
解释:
上图为输入的图。
蓝色边为最优子图之一。
注意,子图 [[1,0,3],[0,5,6]] 也能得到最优解,但无法在满足所有限制的前提下,得到更优解。
示例 2:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-v48CgnNX-1647150289703)(https://assets.leetcode.com/uploads/2022/02/17/example2-1drawio.png)]
输入:n = 3, edges = [[0,1,1],[2,1,1]], src1 = 0, src2 = 1, dest = 2
输出:-1
解释:
上图为输入的图。
可以看到,不存在从节点 1 到节点 2 的路径,所以不存在任何子图满足所有限制。
提示:
3 <= n <= 1050 <= edges.length <= 105edges[i].length == 30 <= fromi, toi, src1, src2, dest <= n - 1fromi != toisrc1,src2和dest两两不同。1 <= weight[i] <= 105
/* 我以为很简单 直接Dijkstra算法就行了! 结果我还是太天真了。
我的想法是:使用Dijkstra算法 1.找到src1 到 dest的最短距离 d1;
2.找到src2 到 dest的最短距离 d2;
3.如果有的话,找到src1 到 src2的最短距离 + d2 = d3;
4. 或者 src2 到 src1的最短距离 + d1 = d4;
返回 d1 + d2, d3, d4 的最大值;
只过了72个测试用例,最后发现,需要考虑路径重合问题!!!!!
*/
// 大神解法: @arignote (https://leetcode-cn.com/u/arignote/) (改变版,原版使用三目等,排版不好看)
// 没看太懂,尬住!
class Solution {
public long minimumWeight(int n, int[][] edges, int src1, int src2, int dest) {
ArrayList<long[]>[] list = new ArrayList[n], list2 = new ArrayList[n];
for (int i = 0; i < n; i++) {
list[i] = new ArrayList<>();
list2[i] = new ArrayList<>();
}
for (int[] edge : edges) {
// 每个索引,存储其子节点
list[edge[0]].add(new long[] { edge[1], edge[2] });
// 每个索引,存储其父节点
list2[edge[1]].add(new long[] { edge[0], edge[2] });
}
//
Long s1[] = minimumWeight(src1, list);
Long s2[] = minimumWeight(src2, list);
Long d[] = minimumWeight(dest, list2),
Long min = Long.MAX_VALUE;
for (int i = 0; i < n; i++) {
if (s1[i] != null && s2[i] != null && d[i] != null) {
min = Math.min(min, s1[i] + s2[i] + d[i]);
}
}
return min < Long.MAX_VALUE ? min : -1;
}
private Long[] minimumWeight(int src, ArrayList<long[]>[] list) {
Long[] dist = new Long[list.length], poll;
// 使用优先级队列(小根堆)
PriorityQueue<Long[]> queue = new PriorityQueue<>((a, b) -> Long.compare(a[0], b[0]));
for (queue.offer(new Long[] { 0L, (long) src }); (poll = queue.poll()) != null;) {
if (dist[poll[1].intValue()] == null) {
dist[poll[1].intValue()] = poll[0];
for (long[] edge : list[poll[1].intValue()]) {
queue.offer(new Long[] { poll[0] + edge[1], edge[0] });
}
}
}
return dist;
}
}
总结: 图算法还需要多实战!!!
如果有大佬看懂了这个或者有更好的解法,麻烦在评论区讲一下,感谢!!!!







 本文总结了LeetCode第284场周赛的四道题目,包括找出数组中的所有K近邻下标、统计可以提取的工件、K次操作后最大化顶端元素和得到要求路径的最小带权子图。文章分析了解题思路,对比了个人解法与优秀解法,强调了熟悉内置函数、图算法和路径重合问题的重要性。
本文总结了LeetCode第284场周赛的四道题目,包括找出数组中的所有K近邻下标、统计可以提取的工件、K次操作后最大化顶端元素和得到要求路径的最小带权子图。文章分析了解题思路,对比了个人解法与优秀解法,强调了熟悉内置函数、图算法和路径重合问题的重要性。
















 311
311

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








