解题--＞在线OJ(十四)

1.二维数组中的查找

1.

解题思路:

class Solution {
     public static boolean findNumberIn2DArray(int[][] matrix, int target) {
        boolean flag=false;
        int i=matrix.length-1;
        int j=0;
        for(;i>=0 && j<matrix[0].length;){
            if(matrix[i][j]==target && i>=0 && j<matrix[0].length){
                flag=true;
                break;
            }else if(matrix[i][j]>target &&i>=0 && j<matrix[0].length){
                i--;
            }else{
                j++;
            }
        }
        return flag;
    }
}

2.从尾到头打印链表

解题思路：
1.先反转链表，然后再遍历链表，将节点值存在数组当中，返回即可。

class Solution {
  public static int[] reversePrint(ListNode head) {
        ListNode temp=head;
        int  length=0;
        while(temp!=null){
            length++;
            temp=temp.next;
        }
        int[] arr=new int[length];
        if(head==null){
            return arr;
        }
        if(head.next==null){
            arr[0]=head.val;
            return arr;
        }
        ListNode pre=head;
        ListNode node=head.next;
        while(node!=null){
            ListNode next=node.next;
            node.next=pre;
            pre=node;
            node=next;
        }
        int i=0;
        while(pre!=null && i<arr.length){
            arr[i++]=pre.val;
            pre=pre.next;
        }
        return arr;
    }
}

3.重建二叉树

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return build(preorder,0,inorder,0,inorder.length-1);
    }
    public TreeNode build(int[] preorder,int rootIndex,int[] inorder,int left,int right){
        if(rootIndex>=preorder.length || left>right){
            return null;
        }
        TreeNode node=new TreeNode(preorder[rootIndex]);
        int i=0;
        for(;i<inorder.length;i++){
            if(inorder[i]==node.val){
                break;
            }
        }
        node.left=build(preorder,rootIndex+1,inorder,left,i-1);
        node.right=build(preorder,rootIndex+i-left+1,inorder,i+1,right);
        return node;
    }
}

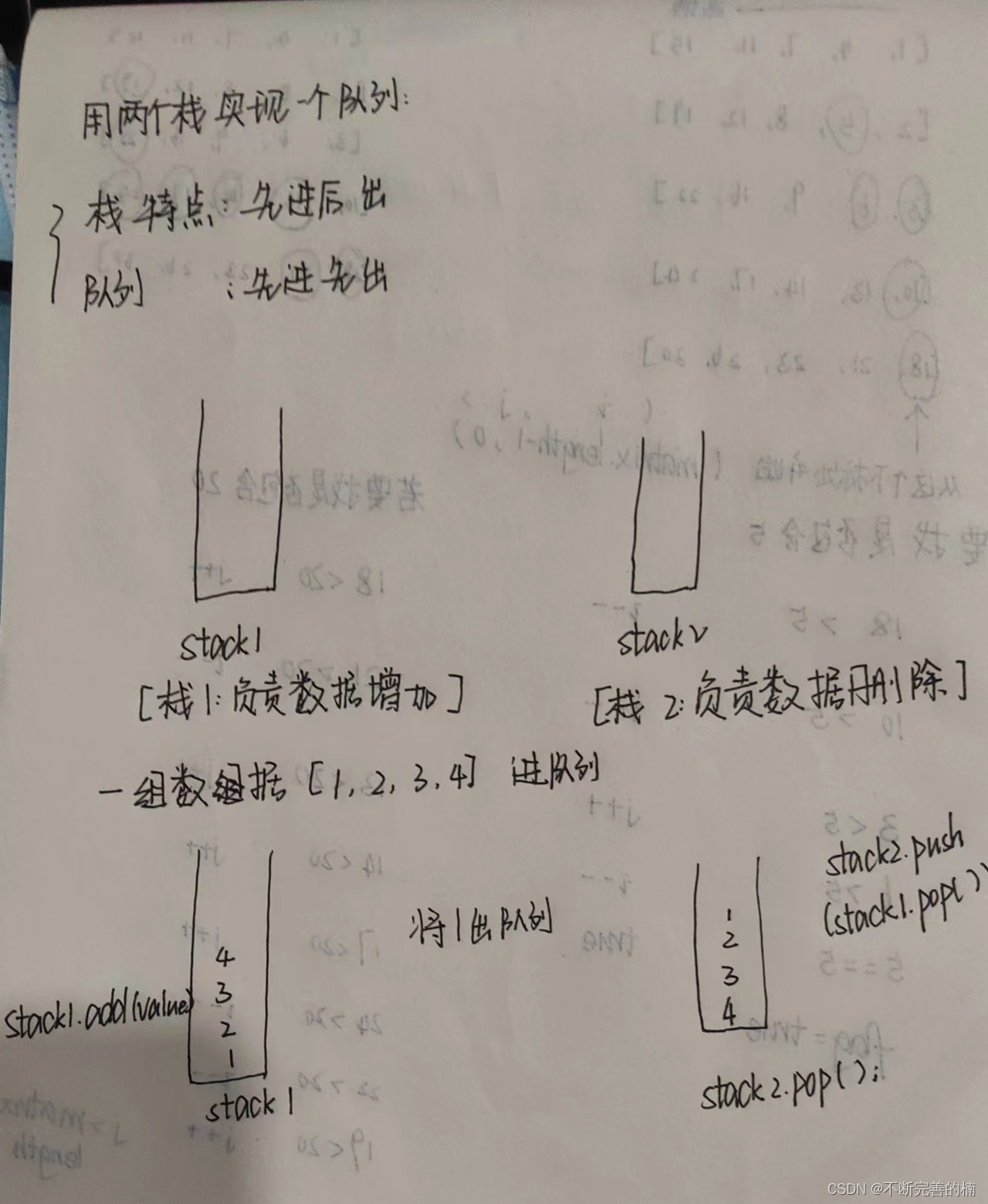
4.用两个栈实现一个队列

解题思路:

class CQueue {
    Stack<Integer> stack1=new Stack<>();
    Stack<Integer> stack2=new Stack<>();
    public void CQueue() {

    }

    public void appendTail(int value) {
        stack1.add(value);
    }

    public int deleteHead() {
      if(stack2.isEmpty()){
          if (stack1.isEmpty()){
              return -1;
          }
          while(!stack1.isEmpty()){
              stack2.push(stack1.pop());
          }
      }
        return stack2.pop();
    }
}

5.斐波那契数列

解题思路：
f(0)=0;
f(1)=1;
f(2)=f(2-1)+f(2-2);
f(n)=f(n-1)+f(n-2);
如果采用递归的方法，会时间超时。
所以采用for循环，来计算出第n项的值
另外:
青蛙跳台和斐波那契数列类似。只是 f(0)=1。

class Solution {
    public int fib(int n) {
        if(n==0){
            return 0;
        }
        if(n==1){
            return 1;
        }
        int a0=0;
        int a1=1;
        int result=0;
        for(int i=2;i<=n;i++){
            result=(a0+a1)%1000000007;
            a0=a1;
            a1=result;
        }
        return a1;
    }
}

6.课程表（207）

解题思路:

class Solution {
    ArrayList<Integer>[] arr;
    int[] visiting;
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        arr=new ArrayList[numCourses];
        visiting =new int[numCourses];
        for(int[] pre:prerequisites){
            int course=pre[0];
            int precourse=pre[1];
            if(arr[course]==null){
                arr[course] = new ArrayList<>();
            }
            arr[course].add(precourse);
        }
        for(int i=0;i<numCourses;i++){
         if(dfs(i)==false){
               return false;
           }
        }
        return true;
    }
    public boolean dfs(int i){
        if(visiting[i]==1){
            return false;
        }
        if(arr[i]==null){
            return true;
        }
        visiting[i]=1;
        for(int x:arr[i]){
            if(dfs(x)==false){
                return false;
            }
        }
        visiting[i]=0;
        arr[i]=null;
        return true;
    }
}

7.完全平方数(279)

class Solution {
    public  static int numSquares(int n) {
        int[] dp=new int[n+1];
        dp[0]=0;
        List<Integer> list=squareNum(n);
        for(int i=1;i<dp.length;i++){
            int min=Integer.MAX_VALUE;
            for(int x:list){
                if(i<x){
                    break;
                }
                min=Math.min(min,dp[i-x]+1);
                dp[i]=min;
            }
        }
        return dp[n];
    }
    public static List<Integer> squareNum(int n){
        List<Integer> list=new ArrayList<>();
        int num=1;
        int add=3;
        while(num<=n){
            list.add(num);
            num=num+add;
            add+=2;
        }
        return list;
    }
}

8.矩阵中的路径

解题思路:

class Solution {
public boolean exist(char[][] board, String word) {
        //将字符串拆分成一个字符数组
        char[] ret=word.toCharArray();
        for(int i=0;i<board.length;i++){
            for(int j=0;j<board[0].length;j++){
                if(dfs(board,i,j,ret,0)){
                    return true;
                }
            }
        }
        return false;
    }
    public boolean dfs(char[][] board,int i,int j,char[] ret,int index){
        //如果 i,j下标小于0，或者大于board数组长度，直接返回false;
        //如果board数组元素和ret数组元素不一致的时候，直接返回false;
        if(i<0 || i>=board.length || j<0 || j>=board[0].length || ret[index]!=board[i][j]){
            return false;
        }
        //如果ret的长度:index==ret.length-1：说明匹配完成，直接返回true即可
        if(index==ret.length-1){
            return true;
        }
        //走到这就说明，board当下对应元素 等于 ret数组当下对应的元素
        //此时，将board当下的元素做个标记
        board[i][j]='#';
        //继续递归
        //按照上左下右的顺序
            boolean flag=dfs(board,i-1,j,ret,index+1)
                    || dfs(board,i,j-1,ret,index+1)
                    || dfs(board,i+1,j,ret,index+1)
                    || dfs(board,i,j+1,ret,index+1);
                     //回退当前矩阵的元素
        board[i][j]=ret[index];
        return flag;
    }
}

9.机器人的运动范围

解题思路:
从(0,0)开始，
先判断下标是否越界和是否已经被访问过
再判断 行坐标和列坐标的数位之和是否小于k
如果下标没有越界，也没有被访问过，行坐标和列坐标的数位之和小于k，这就是符合条件的，count++，然后再递归当前元素的上下左右是否满足条件。

class Solution {
  int count;
    public int movingCount(int m, int n, int k) {
        count=0;
        boolean[][] visiting=new boolean[m][n];
        dfs(0,0,m,n,k,visiting);
        return count;
    }
    //递归,计算当下对应元素的上下左右是否满足条件，并且保证它的上下左右是之前没有被计算过的
    public void dfs(int x,int y, int m,int n,int k,boolean[][] visiting){
        //如果下标越界或者是对应元素已经被访问了，直接返回
        if(x<0 || x>=m ||y<0 ||y>=n ||visiting[x][y]){
            return;
        }
        //如果下标不满足条件，直接返回
        if(!countNum(x,y,k)){
            return;
        }
        //走到这一步，就证明此时下标对应的位置是符合条件的，所以，计数++
        count++;
        //标记此下标，说明此下标的位置已经被访问过了
        visiting[x][y]=true;
        //然后开始遍历当前下标的 上左下右 是否满足条件
        dfs(x-1,y,m,n,k,visiting);
        dfs(x,y-1,m,n,k,visiting);
        dfs(x+1,y,m,n,k,visiting);
        dfs(x,y+1,m,n,k,visiting);

    }
    //判断x下标，y下标的每一位加起来 是否比 给定值k 大
    public boolean countNum(int x,int y,int k){
        int sum=0;
        while(x>0){
            sum+=x%10;
            x/=10;
        }
        while(y>0){
            sum+=y%10;
            y/=10;
        }
        return sum<=k;
    }
}

10.丑数

解题思路:

class Solution {
 public  static int nthUglyNumber(int n) {
        int[] result=new int[n+1];
        result[1]=1;
        int dp_2=1;
        int dp_3=1;
        int dp_5=1;
        for(int i=2;i<result.length;i++){
            int r_2=result[dp_2]*2;
            int r_3=result[dp_3]*3;
            int r_5=result[dp_5]*5;
            result[i]=Math.min(Math.min(r_2,r_3),r_5);
            if(result[i]==r_2){
                dp_2++;
            }
            if(result[i]==r_3){
                dp_3++;
            }
            if(result[i]==r_5){
                dp_5++;
            }
        }
        return result[result.length-1];
    }
}