参数估计（基于R）

首先，参数估计是指用样本统计量去估计总体的参数，参数估计的方法有点估计和区间估计。

• 点估计是用估计量的某个取值来直接作为总体参数的取值，比如用样本均值作为总体均值，样本方差作为总体方差，但点估计无法得到估计的可靠性，也无法说出点估计值与总体参数真实值接近的程度，所以我们应该围绕点估计值构造出总体参数的一个区间
• 区间估计是在点估计的基础上得到总体参数的一个估计区间，该区间通常是由样本统计量加减估计误差得到的。
• 在区间估计中，由样本估计量构造出的总体参数在一定置信水平下的估计区间称为置信区间；假定抽取100个样本构造出100个置信区间，这100个置信区间中有95%的区间包含总体参数的真值，则95%这个值称为置信水平。

一、评量估计量的标准

1.无偏性：指估计量抽样分布的期望值等于被估计的总体参数。

#无偏性
#样本均值、样本中位数和样本方差的无偏性模拟
x<-vector();m<-vector();v<-vector()
n=10
for(i in 1:10000){
  d<-rnorm(n,50,10)
  x<-append(x,mean(d))
  m<-append(m,median(d))
  v<-append(v,var(d))
}
data.frame(mean(x),mean(m),mean(v))

2.有效性：指估计量的方差大小。

#有效性
#计算样本均值的方差和样本中位数的方差
x<-vector();m<-vector()
n=10;
for(i in 1:10000){
  d<-rnorm(n)
  x<-append(x,mean(d))
  m<-append(m,median(d))
}
data.frame(var(x),var(m))

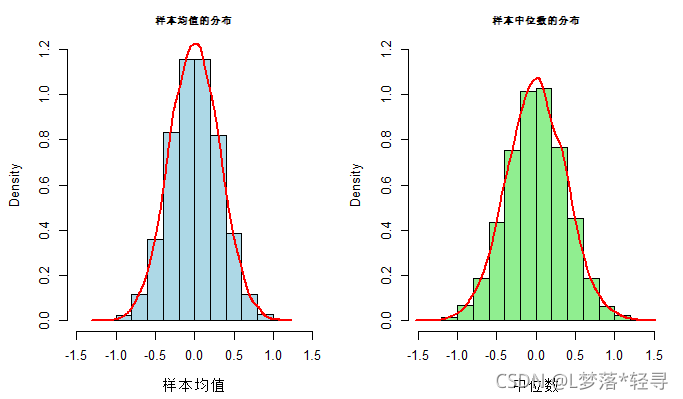
• 我们可以进一步绘制均值和样本中位数分布的直方图，如下：

par(mfrow=c(1,2),mai=c(0.7,0.7,0.4,0.2),cex=0.8)
hist(x,prob=T,col="lightblue",xlim=c(-1.5,1.5),ylim=c(0,1.2),xlab="样本均值",main="样本均值的分布",cex.main=0.8)
lines(density(x),col="red",lwd=2)
hist(m,prob=T,col="lightgreen",xlim=c(-1.5,1.5),ylim=c(0,1.2),xlab="中位数",main="样本中位数的分布",cex.main=0.8)
lines(density(m),col="red",lwd=2)

其结果如图：

3.一致性：指随着样本量无限增大，统计量收敛于所估计的参数，即一个大样本得到的估计量更接近于总体参数。

#一致性
#样本量分别为10,100,500,900时的样本均值
set.seed(12)
N=rnorm(1000,50,10)
mu=mean(N)
xbar10<-mean(sample(N,10,replace=F))
xbar100<-mean(sample(N,100,replace=F))
xbar500<-mean(sample(N,500,replace=F))
xbar900<-mean(sample(N,900,replace=F))
data.frame(总体均值=mu,xbar10,xbar100,xbar500,xbar900)
data.frame("d10"=(xbar10-mu),"d100"=(xbar100-mu),"d500"=(xbar500-mu),"d900"=(xbar900-mu))

二、总体均值的区间估计

1.一个总体均值的估计

• 大样本的估计

#大样本的估计(n>=30)
example5_1<-read.csv("D:/R/example5_1.csv")
library(lattice)
library(BSDA)
z.test(example5_1$耗油量,mu=0,sigma.x=sd(example5_1$耗油量),conf.level=0.90)
z.test(example5_1$耗油量,mu=0,sigma.x=sd(example5_1$耗油量),conf.level=0.90)$conf.int

• 小样本的估计

#小样本的估计(n<30)
example5_2<-read.csv("D:/R/example5_2.csv")
t.test(example5_2,conf.level=0.95)
t.test(example5_2)$conf.int

2.两个总体均值之差的估计

• 独立大样本的估计

#独立大样本的估计
example5_3<-read.csv("D:/R/example5_3.csv")
library(BSDA)
z.test(example5_3$男性工资,example5_3$女性工资,mu=0,sigma.x=sd(example5_3$男性工资),sigma.y=sd(example5_3$女性工资))$conf.int

• 独立小样本的估计

#独立小样本的估计
example5_4<-read.csv("D:/R/example5_4.csv")
t.test(x=example5_4$方法一,y=example5_4$方法二,var.equal=TRUE)$conf.int#方差相等
t.test(x=example5_4$方法一,y=example5_4$方法二,var.equal=FALSE)$conf.int#方差不等

• 配对样本的估计

example5_5<-read.csv("D:/R/example5_5.csv")
t.test(example5_5$试卷A,example5_5$试卷B,paired=TRUE)$conf.int

三、总体比例的区间估计

1.一个总体比例的估计

• 大样本的估计方法

n<-500;x<-325;p<-x/n;q<-qnorm(0.975)
LCI<-p-q*sqrt(p*(1-p)/n)
UCI<-p+q*sqrt(p*(1-p)/n)
data.frame(LCI,UCI)

library(Hmisc)
library(survival)
library(Formula)
library(ggplot2)
library(Hmisc)
binconf(x,n,alpha=0.05,method="all")

注：使用Hmisc包中的binconf函数可以得到三种不同方法的区间：一是利用F分布计算的精确区间；二是基于得分检验的Wison近似置信区间；三是按式计算的大样本正态近似的置信区间。

• 任意大小样本的估计方法

n1<-500+4
p1<-(325+2)/n1
q<-qnorm(0.975)
LCI<-p1-q*sqrt(p1*(1-p1)/n1)
UCI<-p1+q*sqrt(p1*(1-p1)/n1)
data.frame(LCI,UCI)

2.两个总体比例之差的估计

• 两个大样本的估计方法

#两个大样本
p1<-225/500;p2<-128/400
q<-qnorm(0.975)
LCI<-p1-p2-q*sqrt(p1*(1-p1)/500+p2*(1-p2)/400)
UCI<-p1-p2+q*sqrt(p1*(1-p1)/500+p2*(1-p2)/400)
data.frame(LCI,UCI)

• 两个任意大小样本的估计方法

#两个任意大小样本
p1<-(225+1)/(500+2);p2<-(128+1)/(400+2)
q<-qnorm(0.975)
LCI<-p1-p2-q*sqrt(p1*(1-p1)/(500+2)+p2*(1-p2)/(400+2))
UCI<-p1-p2+q*sqrt(p1*(1-p1)/(500+2)+p2*(1-p2)/(400+2))
data.frame(LCI,UCI)

四、总体方差的区间估计

1.一个总体方差的估计

#一个总体方差的估计
example5_2<-read.csv("D:/R/example5_2.csv")
library(Hmisc)
library(BSDA)
library(TeachingDemos)
sigma.test(example5_2$食品重量,conf.level=0.95)$conf.int

2.两个总体方差比的估计

example5_4<-read.csv("D:/R/example5_4.csv")
var.test(example5_4$方法一,example5_4$方法二,alternative="two.sided")$conf.int

五、确定合适的样本量

1.已知：最大容许误差E，总体标准差的估计s，置信度所对应的z值
带入公式n=(z*s/E)^2
例：

z<-qnorm(0.05,low=F)#z<-qnorm(0.95)
s<-2000;E<-100
n<-(z*s/E)^2

2.已知：最大容许误差E，比例估计值p，置信度所对应的z值
带入公式n=p*(1-p)*(z/E)^2