Java 做相关性分析

相关性分析

相关分析是指对两个或多个具备相关性的变量元素进行分析，从而衡量两个因素的的相关密切程度，相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析。

1. 相关系数 相关系数衡量了两个变量的统一程度，范围是-1~1,‘1’代表完全正相关，‘-1’代表完全负相关。比较常用的是Pearson‘皮尔逊’相关系数、Spearman‘斯皮尔曼’相关系数；
2. Pearson相关系数 一般用于分析，两个连续变量之间的关系，是一种线性相关系数；
3. Spearman相关系数 Pearson相关系数要求连续变量的取值服从正态分布，不服从正态分布的变量、分类或等级变量之间的关联性可采用Spearman秩相关系数，也称等级相关系数来描述。；
4. P值 P值即概率，反映某一事件发生的可能性大小。统计学根据显著性检验方法所得到的P 值，一般以P < 0.05 为显著， P<0.01 为非常显著，其含义是样本间的差异由抽样误差所致的概率小于0.05 或0.01；

示例

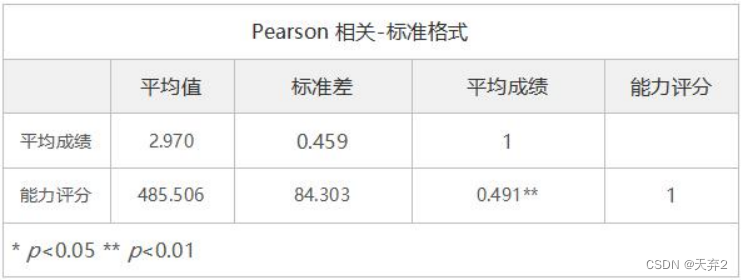
平均成绩和能力评分之间的相关系数为0.491，并且呈现出0.01水平的显著性，因而说明平均成绩和能力评分之间有显著的正相关关系

相关性分析流程

安装依赖

        <dependency>
            <groupId>net.sf.jsci</groupId>
            <artifactId>jsci</artifactId>
            <version>1.2</version>
        </dependency>
        <dependency>
            <groupId>org.apache.commons</groupId>
            <artifactId>commons-math3</artifactId>
            <version>3.6.1</version>
        </dependency>

Java代码

统计工具类

import JSci.maths.statistics.TDistribution;
import org.apache.commons.math3.exception.DimensionMismatchException;
import org.apache.commons.math3.stat.correlation.PearsonsCorrelation;
import org.apache.commons.math3.stat.correlation.SpearmansCorrelation;
import org.apache.commons.math3.stat.descriptive.moment.Mean;
import org.apache.commons.math3.stat.descriptive.moment.StandardDeviation;


/**
 * Statistics
 * 统计工具类，使用统计工具用于做统计学数据分析，将计算方法进行集成调用
 */
public class StatisticsUtil {
    
    private static StatisticsUtil stat;

    private static final double  NOVALUE = Double.NaN;

    private StatisticsUtil() {
    }

    public static StatisticsUtil getInstance() {

        if (stat == null) {
            stat = new StatisticsUtil();
        }
        return stat;
    }

    /**
     * 计算数据均值
     * @param values 双精度数组
     * @return 平均值
     */
    public static double computeMean(final double[] values) {
        if (testNull(values)) {
            return NOVALUE;
        }
        Mean mean = new Mean();
        return mean.evaluate(values);
    }

    /**
     * 计算数据标准差
     * @param values 双精度数组
     * @return 标准差
     */
    public static double computeStandardDeviation(final double[] values) {
        if (testNull(values)) {
            return NOVALUE;
        }
        StandardDeviation sd = new StandardDeviation();
        return sd.evaluate(values);
    }

    /**
     * 获取数据最大值
     * @param values 双精度数组
     * @return 最大值
     */
    public static double getMaxValue(final double[] values) {
        if (testNull(values)) {
            return NOVALUE;
        }
        Arrays.sort(values);
        return values[values.length - 1];
    }


    /**
     * 获取数据最小值
     * @param values 双精度数组
     * @return 最小值
     */
    public static double getMinValue(final double[] values) {
        if (testNull(values)) {
            return NOVALUE;
        }
        Arrays.sort(values);
        return values[0];
    }

    /**
     * 获取数据最大值和最小值
     * @param values - 双精度数组
     * @return map<String, Double>
     */
    public static Map<String, Double> getMaxAndMin(final double[] values) {
        Map<String, Double> result = new HashMap<>(16);
        result.put("max", NOVALUE);
        result.put("min", NOVALUE);
        if (testNull(values)) {
            return result;
        }
        Arrays.sort(values);
        result.clear();
        result.put("max", values[values.length - 1]);
        result.put("min", values[0]);
        return result;
    }

    /**
     * 计算两个数据之间的相关系数
     * @param xArray -- 双精度数组
     * @param yArray -- 双精度数组
     * @param methodId -- 相关系数方法
     * @return double
     */
    public static double correlation(final double[] xArray, final double[] yArray, String methodId) {

        double value = NOVALUE;
        if (xArray.length != yArray.length) {
            throw new DimensionMismatchException(xArray.length, yArray.length);
        } else if (xArray.length < 2) {
            return value;
        } else {
            if (PEARSON_ID.equals(methodId)) {
                PearsonsCorrelation pearsonsCorrelation = new PearsonsCorrelation();
                value = pearsonsCorrelation.correlation(xArray, yArray);
            } else if (SPEARMAN_ID.equals(methodId)) {
                SpearmansCorrelation spearmansCorrelation = new SpearmansCorrelation();
                value = spearmansCorrelation.correlation(xArray, yArray);
            }

        }
        return value;
    }

    /**
     * 计算两个数据之间的相关系数
     * @param xArray -- 双精度数组
     * @param yArray -- 双精度数组
     * @return double
     */
    public static double correlation(final double[] xArray, final double[] yArray) {
        return correlation(xArray, yArray, PEARSON_ID);
    }


    /**
     * 计算显著性p值算法
     * @param rValue 相关系数
     * @param n 分析数据的个数
     * @param methodId 使用的方法
     * @return p-value
     */
    public static double getPValue(final double rValue, final int n, String methodId) {

        if (n < 2) {
            return NOVALUE;
        }
        double pValue = NOVALUE;
        double tValue = ((rValue * Math.sqrt(n-2)) / (Math.sqrt(1 - (rValue * rValue))));
        int free= n-2;
        TDistribution td=new TDistribution(free);
        if (PEARSON_ID.equals(methodId)) {

            double cumulative = td.cumulative(tValue);
            if(tValue>0) {
                pValue=(1-cumulative)*2;
            }else {
                pValue=cumulative*2;
            }

        } else if (SPEARMAN_ID.equals(methodId)) {
            if (n > 500) {
                tValue = (rValue * Math.sqrt(n-1));
            }

            double cumulative = td.cumulative(tValue);
            if(tValue>0) {
                pValue=(1-cumulative)*2;
            }else {
                pValue=cumulative*2;
            }

        }

        return pValue;
    }

    /**
     * 计算显著性p值算法
     * @param rValue 相关系数
     * @param n 分析数据的个数
     * @return p-value
     */
    public static double getPValue(final double rValue, final int n) {
        return getPValue(rValue, n, PEARSON_ID);
    }

    /**
     * 判空
     * @param values 双精度数组
     * @return boolean
     */
    private static boolean testNull(final double[] values) {
        return values == null;
    }

}

常量类

/**
 * 分析统计常量
 */
public class AnalysisConstants {

    /**
     * pearson常量
     */
    public static final String PEARSON_ID = "1001";

    public static final String PEARSON_NAME = "pearson";

    /**
     * spearman常量
     */
    public static final String SPEARMAN_ID = "1002";

    public static final String SPEARMAN_NAME = "spearman";

}

测试

public class CorrTest {

    public static void main(String[] args) {
        double[] x = new double[] { 106,86,100,101,99,103,97,113,112,110};
        double[] y = new double[] { 7,0,27,50,28,29,20,12,6,17};

        final double mean = StatisticsUtil.computeMean(x);

        final double correlation = StatisticsUtil.correlation(x, y, PEARSON_ID);

        final double correlation2 = StatisticsUtil.correlation(x, y, SPEARMAN_ID);

        final double pValue = StatisticsUtil.getPValue(correlation, x.length);

        System.out.println(
                "x的平均值为" + mean + '\n' +
                        "x和y的pearson相关系数为" + correlation + '\n' +
                        "x和y的spearman相关系数为" + correlation2 + '\n' +
                        "x和y的p值为" + pValue
        );

    }



}

测试结果

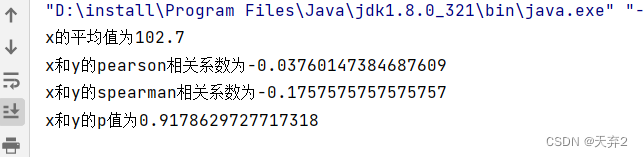
实际工作

做相关性分析需要做一些准备工作，这里给了大致的流程图参考

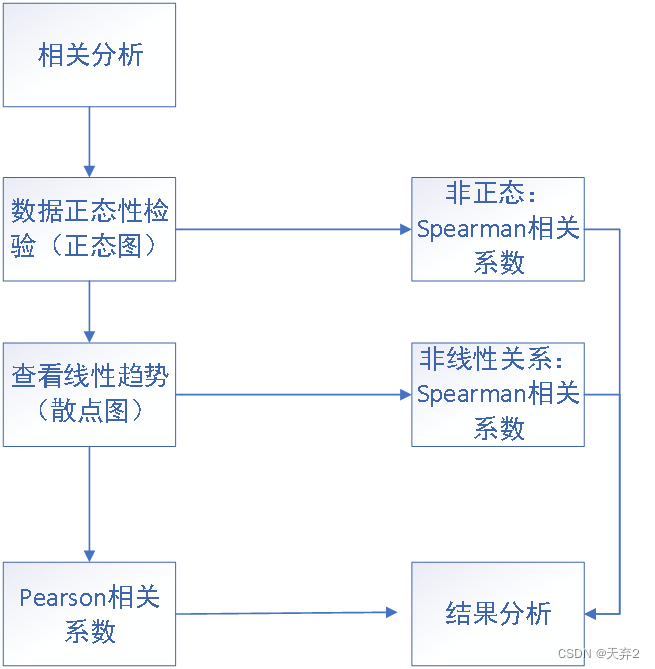
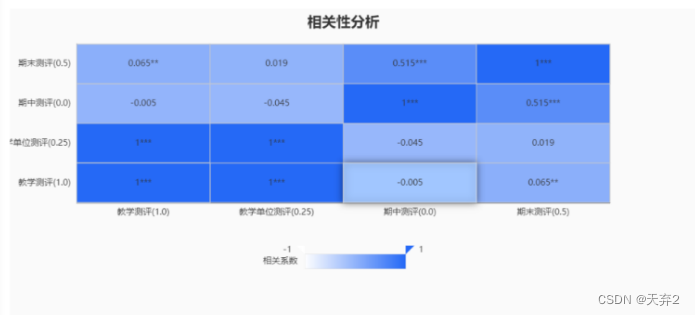
正常来说，相关性分析需要对数据做正态性检验，可以对数据正态频率图检验，业务数据要求对同一类型的数据做分组，再求两个数据之间的相关系数，最后的结果采用echarts的热力图展示

参考

相关分析流程总结 https://www.sohu.com/a/448889275_100103806

Pearson 相关分析 理论与应用 https://blog.youkuaiyun.com/ScapeD/article/details/119515360?spm=1001.2014.3001.5506

java实现皮尔逊相关系数计算 https://blog.youkuaiyun.com/weixin_43861785/article/details/109195963?spm=1001.2014.3001.5506