（图文结合）利用快慢指针判断链表中是否有环和找出环的入口结点的原理剖析

判断链表中是否有环

首先假设有一个无限长的链表，其中slow指针指向链表的第N个结点（结点从0开始），fast指向第0个结点，那么此时fast与slow的距离为N-0=N。

图 1

接下俩采取slow和fast分别采取一次一步和两步的策略移动，设k为移动次数，当k=1即一次移动后则slow与fast距离变为N+1-2=N-1

图 2

继续移动，其总的距离变化：N、N-1、N-2...2、1、0（相遇）

当移动k=N时即移动N次后，fast与slow距离变为0，相遇；

理解了这个，我们再看一个带环链表，其中的环等价于一个无限长的链表，当slow进入环时，fast总会在环中的某个位置。

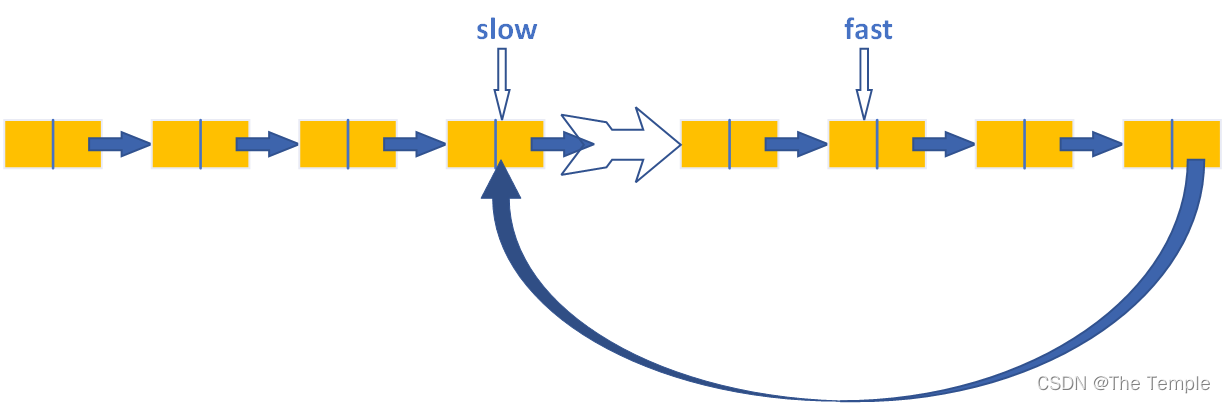
假设此时fast在slow后N位，那么此时与图1的情况类似。同样采取slow一步、fast两步，其总的距离变化也为：N、N-1、N-2...2、1、0（相遇）

由此可知，采取快2、慢1的双指针，如果有环，slow与fast总会在环中相遇。

当fast步频调整为3、4...n时，slow和fast总会相遇吗？（待写）

进一步，其实可以延伸出另一个问题，即寻找环的第一个结点

我们先探究一个问题，当fast与slow相遇时，k=？（可以直接看结论）

设环长为m，非环长n，指针移动如下图所示

 

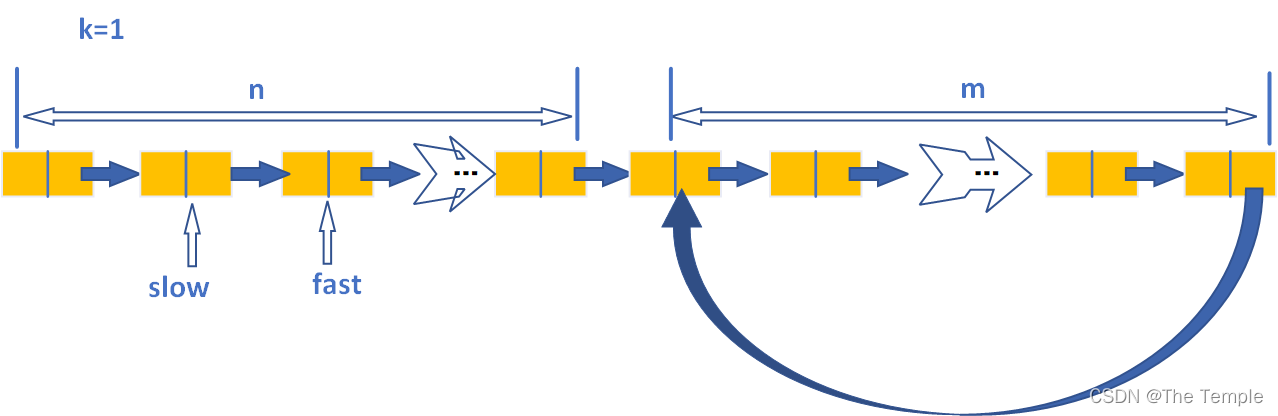
我们可以知道当k=n时，slow指针指向环的入口结点，此时fast走的的步数为2n。（同时我们可以推出slow再走m步又会回到环的起点，即指针走λm+n步时总会指向环的起点）

那么此时fast在slow后的距离为多少？可以分两种情况来讨论

当m>n时，fast仍然是第一次入环，所以其距离环起点（slow所在位置）N=（m+n）-2n=m-n

当m<=n时，其距离环起点距离（slow所在位置）N=（λm+n）-2n=λm-n （λ>=2）由于不知到m与n的具体大小，我们无法判断它是第几次入环

由此可知当k=n,slow位于环入口时，如果想要slow与fast相遇需再移动m-n次或λm-n次

此时k=n+m-n=m或k=n+λm-n=λm

结论：设m为环长,n为非环长，k为移动次数，如果有环当k=m（m>n）或k=λm（m<=n），fast与slow相遇（slow一次一步，fast一次两步）

此时我们可以设置两个指针flag1与flag2，flag1指向链表的起始结点，flag2指向相遇结点，两者均一次一步同时移动，当k=n时，flag1到达环的起始结点，flag2此时相当于走了m+n或λm+n步，同样也到达了起始结点。