【数据结构】树-二叉树、树和森林的还原（图解、c++、java）

已于 2022-07-06 00:27:30 修改
阅读量2.7k 收藏 28
点赞数 6
分类专栏： URLeisure的数据结构之旅 文章标签： 数据结构 c++ java
于 2022-03-05 09:01:45 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/weixin_50564032/article/details/123269869
版权

文章目录

GitHub同步更新（已分类）：Data_Structure_And_Algorithm-Review

公众号：URLeisure 的复习仓库
公众号二维码见文末

以下是本篇文章正文内容，下面案例可供参考。

根据遍历序列可以还原树，包括二叉树还原、树还原和森林还原 3 种。

二叉树的还原

  • 由二叉树的中序序列和前 / 后序序列，或者中序序列和层序序列可以唯一地还原一棵二叉树。

  • 注意：必须包含中序序列才能唯一地还原一棵二叉树。

前中序还原二叉树

1). 算法步骤

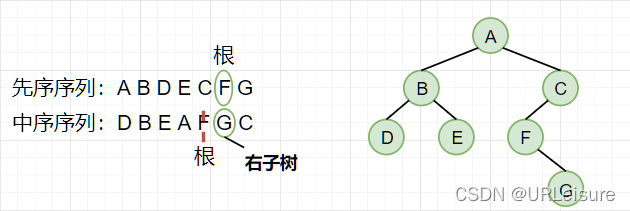
  • 例如：已知一棵二叉树的先序序列 A B D E C F G ABDECFG ABDECFG 和中序序列 D B E A F G C DBEAFGC DBEAFGC，画出二叉树。

算法步骤:

  1. 先序序列的第一个字符为根；
  2. 在中序序列中，以根为中心划分左、右子树；
  3. 还原左、右子树。

2). 图解

  1. 找到先序的第一个字符 A 即为根，在中序中找到根 A 以划分左、右子树。

如图，左子树包含 DBE，右子树包含 FGC。

在这里插入图片描述

  1. 左子树包含 DBE 对应先序序列为 BDE，所以在左子树中字符 B 即为根，在中序中找到根 B 以划分左、右子树。

如图，左子树包含 D，右子树包含 E。

在这里插入图片描述

  1. 右子树包含 FGC 对应先序序列为 CFG，所以在右子树中字符 C 即为根，在中序中找到根 C 以划分左、右子树。

如图，左子树包含 GF，无右子树。

在这里插入图片描述

  1. 左子树包含 GF 对应先序序列为 FG，所以在左子树中字符 F 即为根，在中序中找到根 F 以划分左、右子树。

如图，无左子树，右子树包含 G。

在这里插入图片描述

3). 代码

先解释一下代码中各变量和操作，以便更好的理解代码。

  1. 函数有三个参数，pre 和 mid 为字符串类型，分别指向先序、中序序列的串；len 为序列的长度。前序和中序的序列长度一定是相同的。
  2. 先序序列的第一个字符 pre[0] 为根，然后在中序序列中查找根所在的位置，用 index 记录查找长度，找到后以根为中心，划分出左右子树。

在这里插入图片描述

  • 根据算法步骤可知，每次寻找左、右子树的过程都是相同的，我们可以使用递归求解即可。

c++代码如下（示例）：

void pre_mid_tree(string pre, string mid, int len, Btree &T) {
    if (len == 0) {
        T = nullptr;
        return;
    }
    char ch = pre[0];//得到根
    int index = 0;
    while (mid[index] != ch) {//查找根在中序序列中的位置
        index++;
    }
    T = new BNode;
    T->data = ch;
    pre_mid_tree(pre.substr(1), mid, index, T->lchild);
    pre_mid_tree(pre.substr(index + 1), mid.substr(index + 1), len - index - 1, T->rchild);
}

java代码如下（示例）：

public static Bnode pre_mid_tree(String pre,String mid,int len){
    if(len == 0){
        return null;
    }
    char ch = pre.charAt(0);
    int index = 0;
    while(mid.charAt(index) != ch){
        index ++;
    }
    Bnode t = new Bnode();
   	t.data = ch;
    t.lchild = pre_mid_tree(pre.substring(1),mid,index);
    t.rchild = pre_mid_tree(pre.substring(index+1),mid.substring(index+1),len-index-1);
    return t;
}

中后序还原二叉树

1). 算法步骤

  • 例如：已知一棵二叉树的中序序列 D B E A F G C DBEAFGC DBEAFGC 和后序序列 D E B G F C A DEBGFCA DEBGFCA，画出二叉树。

算法步骤:

  1. 后序序列的最后一个字符为根；
  2. 在中序序列中，以根为中心划分左、右子树；
  3. 还原左、右子树。

2). 图解

  1. 找到后序的最后一个字符 A 即为根，在中序中找到根 A 以划分左、右子树。

如图，左子树包含 DBE，右子树包含 FGC。

在这里插入图片描述

  1. 左子树包含 DBE 对应后序序列为 DEB，所以在左子树中字符 B 即为根，在中序中找到根 B 以划分左、右子树。

如图，左子树包含 D，右子树包含 E。

在这里插入图片描述

  1. 右子树包含 FGC 对应后序序列为 GFC，所以在右子树中字符 C 即为根，在中序中找到根 C 以划分左、右子树。

如图，左子树包含 GF，无右子树。

在这里插入图片描述

  1. 左子树包含 GF 对应后序序列为 GF，所以在左子树中字符 F 即为根，在中序中找到根 F 以划分左、右子树。

如图，无左子树，右子树包含 G。

在这里插入图片描述

3). 代码

先解释一下代码中各变量和操作，以便更好的理解代码。

  1. 函数有三个参数，pro 和 mid 为字符串类型，分别指向后序、中序序列的串；len 为序列的长度。后序和中序的序列长度一定是相同的。
  2. 后序序列的第一个字符 pro[len-1] 为根，然后在中序序列中查找根所在的位置，用 index 记录查找长度，找到后以根为中心，划分出左右子树。

在这里插入图片描述

  • 根据算法步骤可知，每次寻找左、右子树的过程都是相同的，我们可以使用递归求解即可。

c++代码如下（示例）：

void mid_pro_tree(string mid, string pro, int len, Btree &T) {
    if (len == 0) {
        T = nullptr;
        return;
    }
    char ch = pro[len - 1];//得到根
    int index = 0;
    while (mid[index] != ch) {//查找根在中序序列中的位置
        index++;
    }
    T = new BNode;
    T->data = ch;
    mid_pro_tree(mid, pro, index, T->lchild);
    mid_pro_tree(mid.substr(index + 1), pro.substr(index), len - index - 1, T->rchild);
}

java代码如下（示例）：

public static Bnode mid_pro_tree(String mid,String pro,int len){
    if(len == 0){
       	return null;
    }
    char ch = pro.charAt(len-1);
    int index = 0;
    while(mid.charAt(index) != ch){
        index ++;
    }
    Bnode t = new Bnode();
    t.data = ch;
    t.lchild = mid_pro_tree(mid,pro,index);
    t.rchild = mid_pro_tree(mid.substring(index+1),pro.substring(index),len-index-1);
    return t;
}

完整代码

c++代码如下（示例）：

#include<iostream>

using namespace std;

typedef struct BNode {
    char data;
    BNode *lchild, *rchild;
} *Btree;

void pre_mid_tree(string pre, string mid, int len, Btree &T) {
    if (len == 0) {
        T = nullptr;
        return;
    }
    char ch = pre[0];
    int index = 0;
    while (mid[index] != ch) {
        index++;
    }
    T = new BNode;
    T->data = ch;
    pre_mid_tree(pre.substr(1), mid, index, T->lchild);
    pre_mid_tree(pre.substr(index + 1), mid.substr(index + 1), len - index - 1, T->rchild);
}

void mid_pro_tree(string mid, string pro, int len, Btree &T) {
    if (len == 0) {
        T = nullptr;
        return;
    }
    char ch = pro[len - 1];
    int index = 0;
    while (mid[index] != ch) {
        index++;
    }
    T = new BNode;
    T->data = ch;
    mid_pro_tree(mid, pro, index, T->lchild);
    mid_pro_tree(mid.substr(index + 1), pro.substr(index), len - index - 1, T->rchild);
}


int main() {
    Btree T;
    string pre, mid, pro;
    cout << "1.前中序还原\n2.中后序还原\n(输入序号)" << endl;
    int num;
    while (cin >> num) {
        if (num != 1 && num != 2) {
            cout << "输入错误，请重新输入！" << endl;
            continue;
        }
        break;
    }
    cout << "请输入序列：" << endl;
    if (num == 1) {
        cin >> pre >> mid;
        int len = pre.length();
        pre_mid_tree(pre, mid, len, T);
    } else {
        cin >> mid >> pro;
        int len = pro.length();
        mid_pro_tree(mid, pro, len, T);
    }
    return 0;
}
/*
前中序还原：
ABDECFG
DBEAFGC

中后序还原：
DBEAFGC
DEBGFCA
 */

java代码如下（示例）：

import java.util.Scanner;

public class A {
    private static Scanner sc = new Scanner(System.in);

    public static Bnode pre_mid_tree(String pre,String mid,int len){
        if(len == 0){
            return null;
        }
        char ch = pre.charAt(0);
        int index = 0;
        while(mid.charAt(index) != ch){
            index ++;
        }
        Bnode t = new Bnode();
        t.data = ch;
        t.lchild = pre_mid_tree(pre.substring(1),mid,index);
        t.rchild = pre_mid_tree(pre.substring(index+1),mid.substring(index+1),len-index-1);
        return t;
    }

    public static Bnode mid_pro_tree(String mid,String pro,int len){
        if(len == 0){
            return null;
        }
        char ch = pro.charAt(len-1);
        int index = 0;
        while(mid.charAt(index) != ch){
            index ++;
        }
        Bnode t = new Bnode();
        t.data = ch;
        t.lchild = mid_pro_tree(mid,pro,index);
        t.rchild = mid_pro_tree(mid.substring(index+1),pro.substring(index),len-index-1);
        return t;
    }

    public static void main(String[] args) {
        String pre,mid,pro;
        Bnode t = new Bnode();
        System.out.println("1.前中序还原\n2.中后序还原\n(输入序号)");
        int num;
        do{
            num = sc.nextInt();
            if (num != 1 && num != 2) {
                System.out.println("输入错误，请重新输入！");
                continue;
            }
        }while(num != 1 && num != 2);

        System.out.println("请输入序列：");
        if (num == 1) {
            pre = sc.next();
            mid = sc.next();
            int len = pre.length();
            t = pre_mid_tree(pre, mid, len);
        } else {
            mid = sc.next();
            pro = sc.next();
            int len = pro.length();
            t = mid_pro_tree(mid, pro, len);
        }
    }

    private static class Bnode{
        char data;
        Bnode lchild,rchild;
    }
}
/*
前中序还原：
ABDECFG
DBEAFGC

中后序还原：
DBEAFGC
DEBGFCA
 */

树的还原

  • 由于树的先根遍历和后根遍历与其对应的二叉树的先序遍历和中序遍历相同，因此可以根据该对应关系，先还原为二叉树，然后再把二叉树转换成树。

1). 算法步骤

算法步骤:

  1. 根据先根遍历和后根遍历，通过上述的 pre_mid_tree() 方法还原二叉树。
  2. 将二叉树转换成树。

2). 图解

森林的还原

  • 由于森林的先序遍历和中序遍历与其对应的二叉树的先序遍历和中序遍历相同，因此可以根据该对应关系，先还原为二叉树，然后再把二叉树转换成森林。

1). 算法步骤

算法步骤:

  1. 根据先序遍历和中序遍历，通过上述的 pre_mid_tree() 方法还原二叉树。
  2. 将二叉树转换成森林。

2). 图解

总结

  • 要还原唯一二叉树必须要有中序遍历。
关注公众号，感受不同的阅读体验

请添加图片描述

下期预告：哈夫曼树

评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

扑腾的江鱼

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值