【数据结构】树-二叉树的遍历（动态图解、c++、java、递归、多思路非递归）

已于 2022-07-06 00:12:54 修改
阅读量1.3k 收藏 8
点赞数 3
分类专栏： URLeisure的数据结构之旅 文章标签： java 数据结构 c++ 二叉树 算法
于 2022-01-30 19:02:21 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/weixin_50564032/article/details/122587338
版权

文章目录

GitHub同步更新（已分类）：Data_Structure_And_Algorithm-Review

公众号：URLeisure 的复习仓库
公众号二维码见文末

以下是本篇文章正文内容，下面案例可供参考。

二叉树的遍历

  • 二叉树的遍历就是按照某条搜索路径访问二叉树中的每个节点依次且只有一次。

  • 访问的含义很广，如输出、查找、插入、删除、修改、运算等，都可以称为访问。遍历是由顺序的。

  • 一棵二叉树是由根、左子树和右子树构成的。

  • 按照根、左子树和右子树的访问先后顺序不同，二叉树的遍历可以有6种方案：
    D L R 、 L D R 、 L R D 、 D R L 、 R D L 、 R L D DLR、LDR、LRD、DRL、RDL、RLD DLR、LDR、LRD、DRL、RDL、RLD

  • 如果限定先左后右（先左子树后右子树），则只有前3种遍历方案：DLR、LDR、LRD。

  • 按照根的访问顺序不同，分别称为先序遍历（DLR）、中序遍历（LDR）、后序遍历（LRD） 。

  • 因为树的定义本身就是递归的，因此树和二叉树的基本操作用递归算法很容易实现。

递归代码

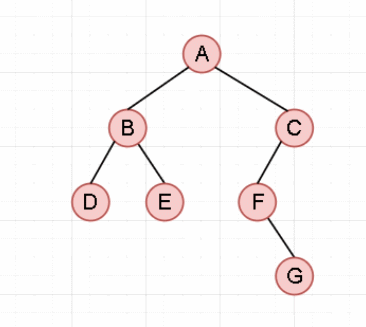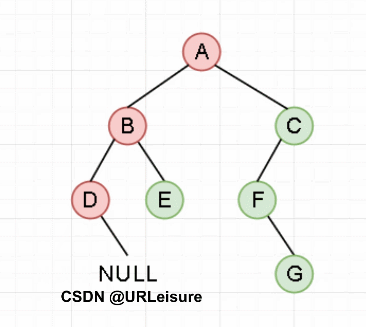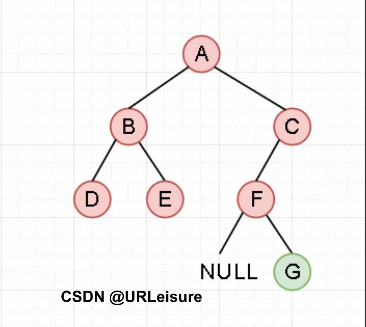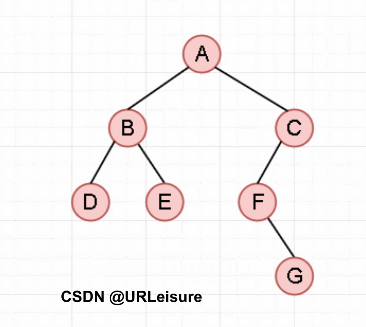
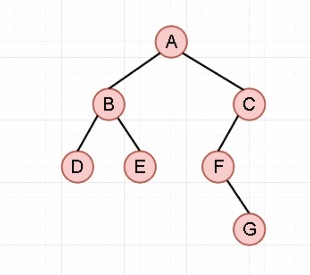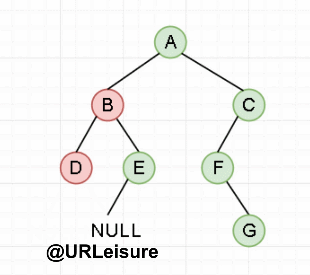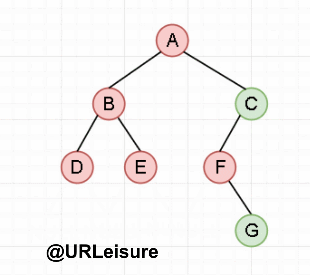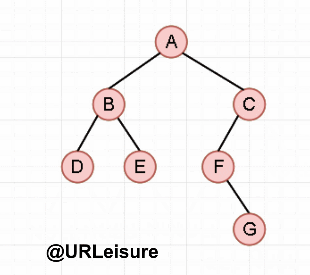
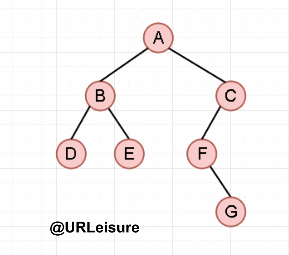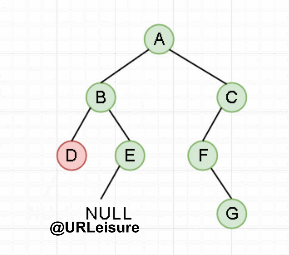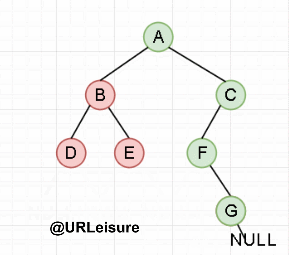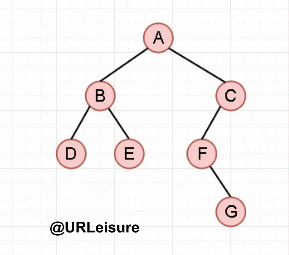
以此二叉树为例：

示例

先序遍历

算法步骤：

如果二叉树不为空，则：

  1. 访问根节点；
  2. 先序遍历左子树；
  3. 先序遍历右子树。

{重复访问节点与向左递归，直到走到最左子，然后向右一次；重复之前操作（右为空，此级递归结束，返回上一级）}
先序

c++代码如下（示例）：

void preOrder(Btree T){
    if(T){
        cout<<T->data<<" ";
        preOrder(T->lchild);
        preOrder(T->rchild);
    }
}

java代码如下（示例）：

public void preOrder(BNode T){
    if(T != null){
        System.out.print(T.data);
        preOrder(T.lchild);
        preOrder(T.rchild);
   	}
}

中序遍历

算法步骤：

如果二叉树不为空，则：

  1. 中序遍历左子树；
  2. 访问根节点；
  3. 中序遍历右子树。

{先去到最左子，访问节点，然后向右一次；重复之前操作（右为空，此级递归结束，返回上一级）}

中序

c++代码如下（示例）：

void inOrder(Btree T){
    if(T){
        inOrder(T->lchild);
        cout<<T->data<<" ";
        inOrder(T->rchild);
    }
}

java代码如下（示例）：

public void inOrder(BNode T){
    if(T != null){
        preOrder(T.lchild);
        System.out.print(T.data);
        preOrder(T.rchild);
    }
}

后序遍历

算法步骤：

如果二叉树不为空，则：

  1. 后序遍历左子树；
  2. 后序遍历右子树；
  3. 访问根节点。

{先去到当前节点的最左子，向右一次；重复之前操作，直到右子为空，访问节点（此级递归结束，返回上一级）}

后续
c++代码如下（示例）：

void postOrder(Btree T){
    if(T){
        postOrder(T->lchild);
        postOrder(T->rchild);
        cout<<T->data<<" ";
    }
}

java代码如下（示例）：

public void postOrder(BNode T){
    if(T != null){
        preOrder(T.lchild);
        preOrder(T.rchild);
        System.out.print(T.data);
    }
}

非递归代码

  • 非递归会用到栈和队列。

  • 非递归写法有好几种吧，感觉从不同角度思考就能写出不同的代码。

先上两种。

  • 个人比较喜欢思路二。

以此二叉树为例：
示例

思路一

先序遍历

  • 我们的非递归-先序遍历是运用栈（栈在STL中是用双端队列实现的）的后进先出特性来达到目的。

算法步骤：

  1. 将根节点放入 stack 中；
  2. 遍历栈，如果 stack 不为空，pop 栈顶节点；
  3. 如果当前 pop 的节点右子不为空，将右子放入 stack中；
  4. 如果当前 pop 的节点左子不为空，将左子放入 stack中。

先序
c++代码如下（示例）：

void preOrder(Btree T){
    if(!T) {//鲁棒
        return;
    }
    Btree tmp;
    stack<Btree> s;
    s.push(T);
    while(!s.empty()){
        tmp = s.top();
        s.pop();
        
        cout<<tmp->data<<" ";
        
        if(tmp->rchild){
            s.push(tmp->rchild);
        }
        if(tmp->lchild){
            s.push(tmp->lchild);
        }
    }
}

java代码如下（示例）：

public static void preOrder(BNode T){
 	if(T == null){
        return;
    }
    BNode tmp;
    Stack<BNode> stack = new Stack<>();
    stack.push(T);
    while(!stack.empty()){
        tmp = stack.pop();//java有返回出栈元素，c++没有
		
		System.out.print(tmp.data + " ");
        
        if(tmp.rchild != null){
            stack.push(tmp.rchild);
        }
        if(tmp.lchild != null){
            stack.push(tmp.lchild);
        }
    }
}

中序遍历

  • 我们的非递归-中序遍历同样是运用栈来达到目的。

算法步骤：

  1. 将根节点设为最新节点放入 stack 中；
  2. 通过递推，将最新节点的所有左子全部放入 stack；
  3. pop最后一个左子，并将该节点的右子设为最新节点；
  4. 然后重复 1、2 直到 stack 为空。

在这里插入图片描述

  • 从图中和代码可以看出：在入栈前和栈底节点出栈后存在空栈状态，所以不能仅以栈是否为空判断终止。

c++代码如下（示例）：

void inOrder(Btree T){
    if(!T){
        return ;
    }
    stack<Btree> s;
    Btree tmp,cur = T;
    while(!s.empty() || cur){
        while(cur){
            s.push(cur);
            cur = cur->lchild;
        }
        tmp = s.top();
        s.pop();
        cout<<tmp->data<<" ";
        if(tmp->rchild){
            cur = tmp->rchild;
        }
    }
}

java代码如下（示例）：

public static void inOrder(BNode T){
    if(T == null){
        return ;
    }

    BNode tmp,cur = T;
    Stack<BNode> stack = new Stack<>();
    while(!stack.empty() || cur != null){
     	while(cur != null){
        	stack.push(cur);
       		cur = cur.lchild;
       	}
        tmp = stack.pop();
        System.out.print(tmp.data + " ");
        if(tmp.rchild != null){
            cur = tmp.rchild;
        }
    }
}

后序遍历

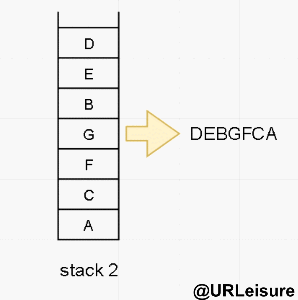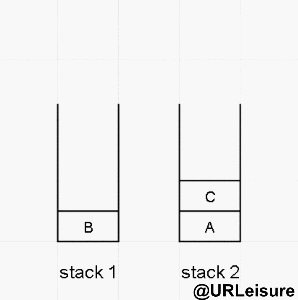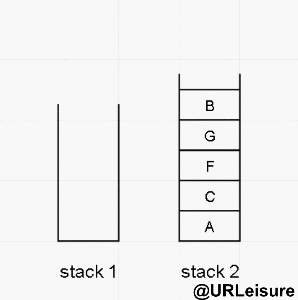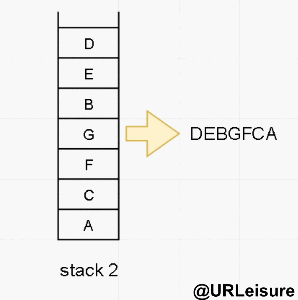
  • 我们的非递归-后序遍历是运用两个栈来达到目的。

算法步骤：

  1. 将节点放入 stack1 中，stack1 进行 pop 操作，将 pop 的节点放入 stack2 中，作为底层；
  2. 将刚才 pop 的节点的左右节点依次放入 stack1 中，先放左节点，再放右节点。
  3. stack2 出栈完成后序遍历输出结果。

后续

c++代码如下（示例）：

void postOrder(Btree T){
    if(!T){
        return ;
    }
    stack<Btree> s1,s2;
    Btree p;
    s1.push(T);
    while(!s1.empty()){
        p = s1.top();
        s2.push(p);
        s1.pop();
        if(p->lchild){
            s1.push(p->lchild);
        }
        if(p->rchild){
            s1.push(p->rchild);
        }
    }
    while(!s2.empty()){
        cout<<s2.top()->data<<" ";
        s2.pop();
    }
}

java代码如下（示例）：

public static void postOrder(BNode T){
    if(T == null){
        return ;
    }
    BNode p;
    Stack<BNode> s1 = new Stack<>();
    Stack<BNode> s2 = new Stack<>();
    s1.push(T);
 	while(!s1.empty()){
        p = s1.pop();
        s2.push(p);
        if(p.lchild != null){
            s1.push(p.lchild);
        }
        if(p.rchild != null){
            s1.push(p.rchild);
        }
    }
    while(!s2.empty()){
        System.out.print(s2.pop().data + " ");
    }
}

思路二

  • 直接模拟的递归思路敲代码。

  • 都要用到栈。

先序遍历

步骤图都一样。
先序

c++代码如下（示例）：

void preOrder(Btree T){
    if(!T){
        return ;
    }
    stack<Btree> s;
    Btree p,cur = T;
    while(!s.empty() || cur){
        while(cur){
            cout<<cur->data<<" ";
            s.push(cur);
            cur = cur->lchild;
        }
        p = s.top();
        s.pop();
        if(p->rchild){
            cur = p->rchild;
        }
    }
}

java代码如下（示例）：

public static void preOrder(BNode T){
    if(T == null){
        return ;
    }
    BNode p,cur = T;
    Stack<BNode> stack = new Stack<>();
  	while(!stack.empty() || cur != null){
        while(cur != null){
            System.out.print(cur.data + " ");
            stack.push(cur);
            cur = cur.lchild;
        }
        p = stack.pop();
        if(p.rchild != null){
            cur = p.rchild;
    	}
    }
}

也能这么写：

void preOrder(Btree T){
    if(!T){
        return ;
    }
    stack<Btree> s;
    Btree p,cur = T;
    while(!s.empty() || cur){
        if(cur){
            cout<<cur->data<<" ";
            s.push(cur);
            cur = cur->lchild;
        }else{
        	p = s.top();
       	 	s.pop();
            cur = p->rchild;
        }
    }
}

中序遍历

步骤图都一样。
中序

c++代码如下（示例）：

void inOrder(Btree T){
    if(!T){
        return false;
    }
    stack<Btree> s;
    Btree p,cur = T;
    while(!s.empty() || cur){
        while(cur){
            s.push(cur);
            cur = cur->lchild;
        }
        p = s.top();
        s.pop();
        cout<<p->data<<" ";
        if(p->rchild){
            cur = p->rchild;
        }
    }
}

java代码如下（示例）：

public static void inOrder(BNode T) {
	if (T == null) {
       	return ;
    }
    BNode p,cur = T;
    Stack<BNode> stack = new Stack<>();
    while(!stack.empty() || cur!=null){
   		while(cur != null) {
        	stack.push(cur);
        	cur = cur.lchild;
    	}
    	p = stack.pop();
    	System.out.print(p.data + " ");
	    if(p.rchild != null){
    	    cur = p.rchild;
    	}
    }
}

也能这么写：

void inOrder(Btree T){
    if(!T){
        return;
    }
    stack<Btree> s;
    Btree p,cur = T;
    while(!s.empty() || cur){
        if(cur){
            s.push(cur);
            cur = cur->lchild;
        }else{
        	p = s.top();
        	s.pop();
        	cout<<p->data<<" ";
            cur = p->rchild;
        }
    }
}

后序遍历

步骤图都一样。

后续
c++代码如下（示例）：

void postOrder(Btree T){
    if(!T){
        return ;
    }
    stack<Btree> s;
    Btree pre,p,cur = T;
    while(!s.empty() || cur){
        while(cur){
            s.push(cur);
            cur = cur->lchild;
        }
        p = s.top();
        s.pop();
        if(!p->rchild || p->rchild==pre){//判断此节点是否有 或 是否输出过的右子
            cout<<p->data<<" ";
            pre = p;
        }else {
            s.push(p);//p不是要输出的对象，再装回去
            cur = p->rchild;
        }
    }
}

java代码如下（示例）：

public static void postOrder1(BNode T) {
    if (T == null) {
        return ;
    }
    BNode p, cur = T;
    BNode pre = null;
    Stack<BNode> stack = new Stack<>();
 	while(!stack.isEmpty() || cur!=null){
        while(cur != null){
            stack.push(cur);
            cur = cur.lchild;
        }
        p = stack.pop();
        if(p.rchild==null || p.rchild == pre){
            System.out.print(p.data + " ");
            pre = p;
        }else{
            stack.push(p);
            cur = p.rchild;
      	}
    }
}

也能这么写：

void postOrder(Btree T){
    if(!T){
        return ;
    }
    stack<Btree> s;
    Btree pre,p,cur = T;
    while(!s.empty() || cur){
        if(cur){
            s.push(cur);
            cur = cur->lchild;
        }else{
        	p = s.top();
        	s.pop();
        	if(!p->rchild || p->rchild==pre){//没有右子 或 右子已被遍历
            	cout<<p->data<<" ";
            	pre = p;
        	}else {
            	s.push(p);//p不是要输出的对象，再装回去
            	cur = p->rchild;
        	}
        }
    }
}

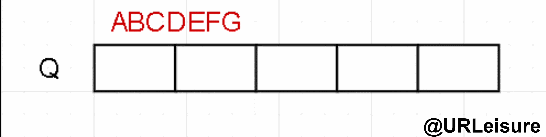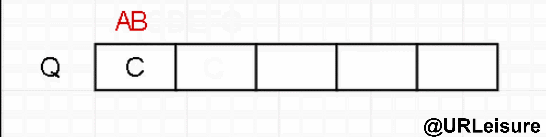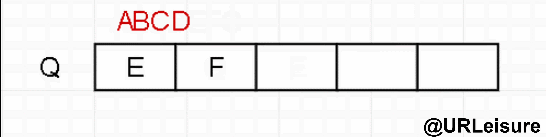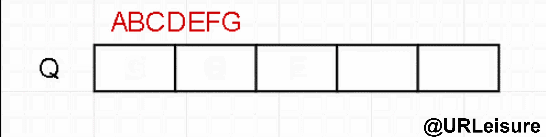
层序遍历

  • 层序跟前中后不同，需要用到队列。

算法步骤：

  1. 节点入队；
  2. 队头元素出队，在判断是否有左右子，依次入队。

在这里插入图片描述

c++代码如下（示例）：

bool leveOrder(Btree T){
    if(!T){
        return false;
    }
    queue<Btree> q;
    Btree p;
    q.push(T);
    while(!q.empty()){
        p = q.front();
        cout<<p->data<<" ";
        q.pop();
        if(p->lchild){
            q.push(p->lchild);
        }
        if(p->rchild){
            q.push(p->rchild);
        }
    }
    return true;
}

java代码如下（示例）：

public static void leveOrder(BNode T){
  	LinkedList<BNode> queue = new LinkedList<>();
    BNode p;
    queue.add(T);
    while(!queue.isEmpty()){
        p = queue.pop();
        System.out.print(p.data + " ");
        if(p.lchild != null){
            queue.add(p.lchild);
        }
        if(p.rchild != null){
            queue.add(p.rchild);
       	}
    }
}
关注公众号，感受不同的阅读体验

请添加图片描述

下期预告：线索二叉树

提前祝大家新年快乐！！！

评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

扑腾的江鱼

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值