快速排序递归实现

快排思路

绝大多数树的排序算法，都可以先理解每趟排序然后再理解多趟排序，快速排序也不例外。下面我将介绍快速排序中单趟排序的三个方法及思路，分别是 左右指针法，挖坑法，前后指针法。

1.左右指针法

快速排序的每一趟都是为了找出值为key的元素的正确位置。而key是一个随机的元素值。

left是从左往右走找比key大的，right是从右往左走找比key小的。然后交换两个元素的值。

多次寻找后，最终left和right相遇

将相遇位置的元素和key的交换，这样就找到key的正确位置，key的坐左边元素都小于它，且右边元素都大于它

那这样一趟排序就结束了。若再将刚刚已经找到正确位置的key的左右区间均进行相同的单趟排序，这样在左右区间的某个元素又可以找到合适的位置。再进行多趟排序好每个元素都可以找到正确位置，那整个数组也就排好序了。

代码的实现

//对 [left，right]区间的元素进行排序
void QSort(int *a, int left, int right)
{
	//left > right 说明待排序的区间不存在则不进行排序
	//left = right 说明区间只有一个元素可以认为是有序也不行排序.
	if (left >= right)
	{
		return;
	}

	//先对[left,right]区间的元素单趟排序，找到key的正确位置
	int midIndex = PartSort1(a, left, right);

	//再对左区间[left,midIndex -1]的元素进行排序
	QSort(a, left, midIndex - 1);

	//最后对右区间[mid +1,right]的元素进行排序
	QSort(a, midIndex + 1,right);
}

//左右指针法
int PartSort1(int *a, int left, int right)
{
	//三数取中,保证right位置处的元素不是最大或最小的，避免了排好序后key的左右区间只存在一个。
	//最终说时间复杂度时会解释.
	int mid = GetMidIndex(a, left, right);
	Swap(&a[mid], &a[right]);

	//key每次都取数组的最后一个元素
	int keyIndex = right;

	//从左往右找比key大的，从右往左找比key小的,交换两者位置
	while (left < right)
	{
		//这里只能时left先走，right后走这样才能保证相遇位置的元素是大于key的
		//最终交换后这个元素就出现再key右边.
		while (left < right && a[left] <= a[keyIndex])
		{
			left++;
		}
		while (left < right && a[right] >= a[keyIndex])
		{
			right--;
		}

		//找到后交换
		Swap(&a[left], &a[right]);
	}

	//将key和相遇位置元素交换
	Swap(&a[left], &a[keyIndex]);
	return left;
}

2.挖坑法

将最后一个元素保存在key中，这样最后一个位置就空出来可以被覆盖，认为它是一个坑

left从左往右走找比key大的，然后填到右边的’坑’。这样在left位置又形成一个新的‘坑’

然后让right从右往左走找比key小的，填到left的‘坑’，这样在right位置再一次形成一个‘坑’.

就这样反复下去，直到left和right相遇。则一趟排序结束，将key填到最后相遇位置的坑.

//对 [left，right]区间的元素进行排序
void QSort(int *a, int left, int right)
{
	//left > right 说明待排序的区间不存在则不进行排序
	//left = right 说明区间只有一个元素可以认为是有序也不行排序.
	if (left >= right)
	{
		return;
	}

	//先对[left,right]区间的元素单趟排序，找到key的正确位置
	int midIndex = PartSort2(a, left, right);

	//再对左区间[left,midIndex -1]的元素进行排序
	QSort(a, left, midIndex - 1);

	//最后对右区间[mid +1,right]的元素进行排序
	QSort(a, midIndex + 1,right);
}

//挖坑法
int PartSort2(int *a, int left, int right)
{
	//三数取中,保证right位置处的元素不是最大或最小的
	int mid = GetMidIndex(a, left, right);
	Swap(&a[mid], &a[right]);

	int key = a[right];//把最右边的元素保存在key中,右边就是一个坑

	while (left < right)
	{
		//从左边开始找比key大的
		while (left < right && a[left] <= key)
		{
			left++;
		}
		//找到后填到右边的坑,这样左边就形成了一个坑
		a[right] = a[left];

		//从右边往左找比key小的
		while (left < right && a[right] >= key)
		{
			right--;
		}
		//找到后填到左边的坑，这样右边又形成了一个坑
		a[left] = a[right];
	}

	//key填到最后left和rigright相遇位置的坑
	a[left] = key;
	return left;
}

3.前后指针法

前指针是cur，后指针是prev初始时的位置是这样的，prev+1=cur。

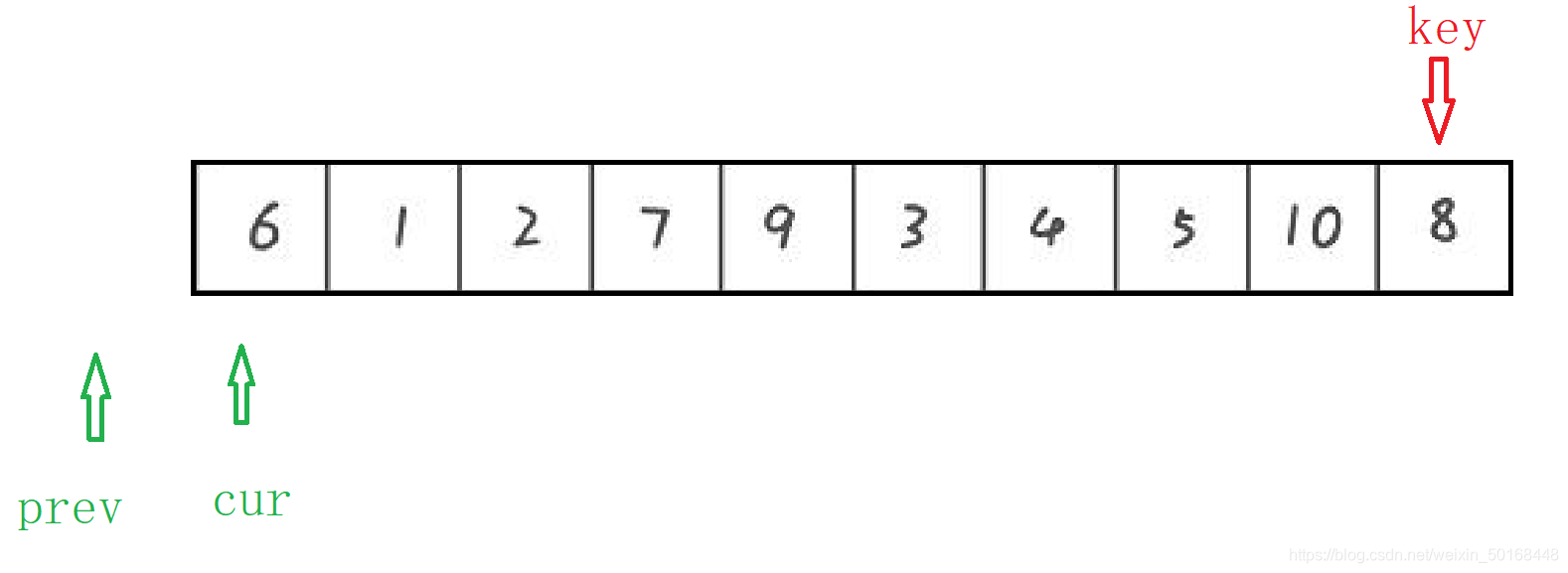
然后cur每次都向右走一步，如果当前元素的值比key小则交换到prev+1的位置处，然后再让prev向右一步走(prev+1 = cur的话，此时prev+1处的元素就是该元素，那么就只让prev向右走而不用交换到prev+1位置处)。

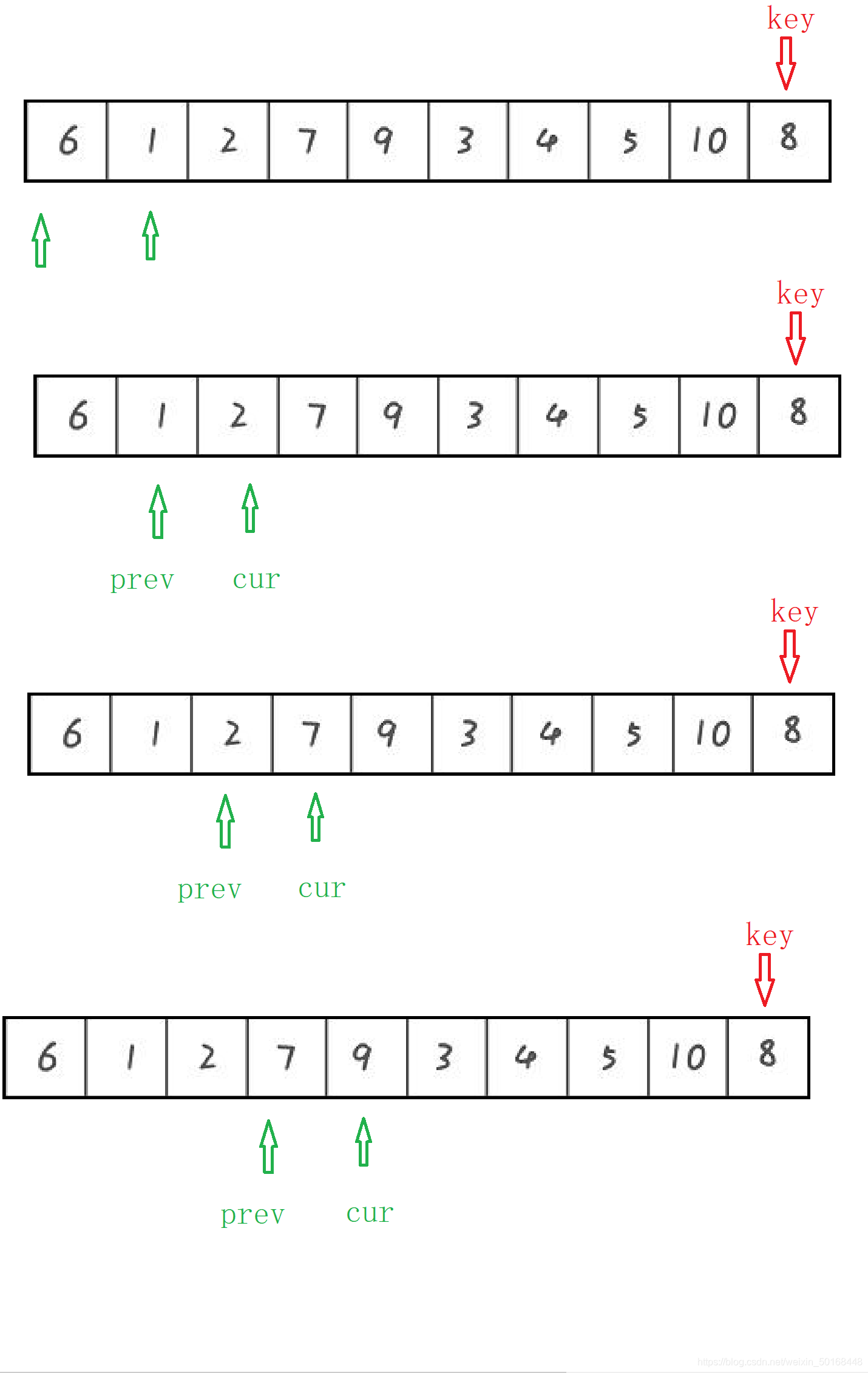
如果当前元素的值比key大，那么cur继续向右走而prev此时位置不变。

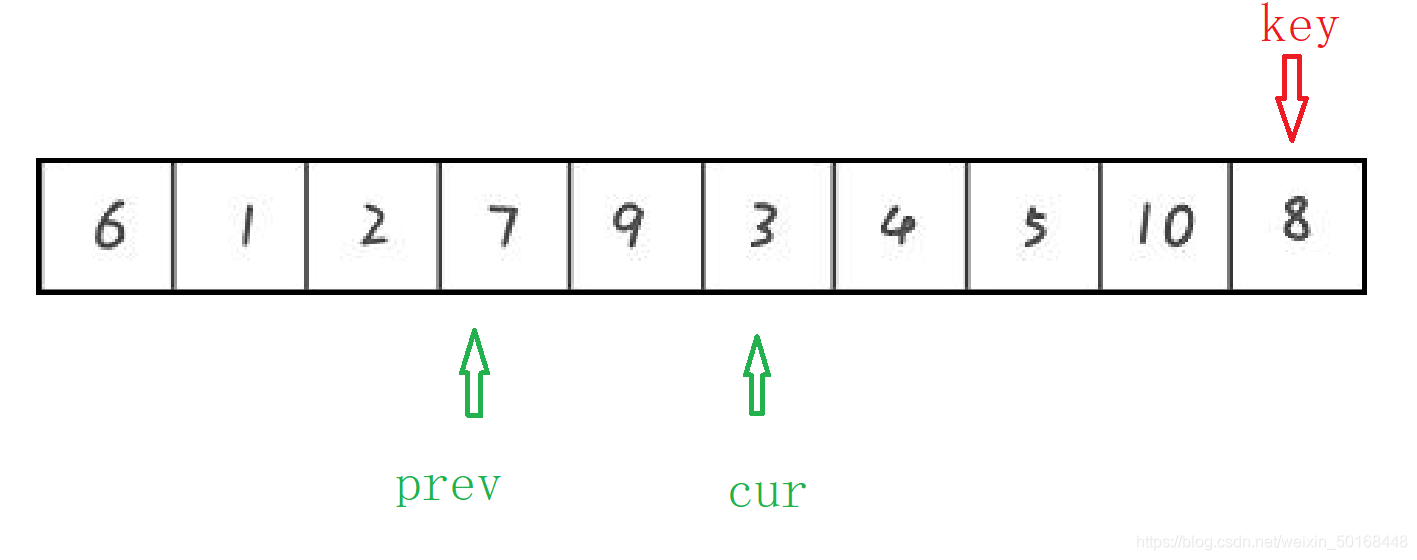
就这样反复走，知道cur走到最后一个元素的位置处，因为key就是最后一个元素，那么把它交换到prev+1位置处就结束了这样的一趟排序。

//对 [left，right]区间的元素进行排序
void QSort(int *a, int left, int right)
{
	//left > right 说明待排序的区间不存在则不进行排序
	//left = right 说明区间只有一个元素可以认为是有序也不行排序.
	if (left >= right)
	{
		return;
	}

	//先对[left,right]区间的元素单趟排序，找到key的正确位置
	int midIndex = PartSort3(a, left, right);

	//再对左区间[left,midIndex -1]的元素进行排序
	QSort(a, left, midIndex - 1);

	//最后对右区间[mid +1,right]的元素进行排序
	QSort(a, midIndex + 1,right);
}

//前后指针法
int PartSort3(int *a, int left, int right)
{
	//三数取中,保证right位置处的元素不是最大或最小的
	int mid = GetMidIndex(a, left, right);
	Swap(&a[mid], &a[right]);

	int keyIndex = right;

	int cur = left;
	int prev = left - 1;

	while (cur < right)
	{
		//比key
		if (a[cur] < a[keyIndex])
		{
			//若prev+1 == cur 则不需要交换,因为此时prev+1和cur位置相同元素也相同.
			if (cur != prev+1)
			{
				Swap(&a[cur], &a[prev+1]);
			}
			cur++;
			prev++;
		}
		else
		{
			cur++;
		}
	}
	//可以看下这段代码的另一种写法
	/*while (cur < right)
	{
		if (a[cur] < a[keyIndex] &&  ++prev != cur)
		{
			Swap(&a[cur], &a[prev]);
		}
		cur++;
	}*/

	//把key交换到prev+1位置处
	Swap(&a[prev + 1], &a[keyIndex]);
	return prev + 1;
}

快排时间复杂度分析

快速排序算法如果每次找到key后都能将区间分成两部分，那时间复杂度就是这样的。

递归调用的每一层时间复杂度都可以认为是O(N)，树总共右logN层。但是找到每次找到的key都是最大或最小的数，那就只能将区间分成一份，另一份就是不存在的。这时的递归调用就是这样的：

这样数的高度就变成 N ，总的时间复杂度就是O(N*N)。
但是如果加上三树取中算法，就可以每次都将数值不是最大也不是最小的数放到最后一个位置，也就保证了key值每次都不是最大或最小值。

三数取中算法

//将数组中取三个数进行比较，最后返回数值大小不是最大也不是最小的那个元素的下标
//这三个数分别是 a[left] a[right] a[(left+right) / 2]
int GetMidIndex(int *a, int left, int right)
{
	int mid = (left + right) / 2;
	if (a[mid] < a[left])
	{
		if (a[mid] < a[right])
		{
			if (a[left] < a[right])
			{
				return left;
			}
			else
			{
				return right;
			}
		}
		else
		{
			return mid;
		}
	}
	else
	{
		if (a[mid] >= a[right])
		{
			if (a[left] >= a[right])
			{
				return left;
			}
			else
			{
				return right;
			}
		}
		else
		{
			return mid;
		}
	}
}