Neural Network 神经网络

DataLaboratory

已于 2024-07-28 22:20:48 修改

阅读量4.2k

点赞数 6

分类专栏： Deep Learning 文章标签： python 深度学习神经网络

于 2022-03-31 22:01:49 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_49742236/article/details/123876304

版权

Deep Learning 专栏收录该内容

1 篇文章

订阅专栏

该博客介绍了如何构建一个基础的三层神经网络模型，采用Sigmoid激活函数。通过前向传播和反向传播，模型在迭代过程中不断调整权重，降低误差。最终，随着迭代次数增加，误差逐渐减小，表明模型训练有效。完整代码已上传至Github。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Neural Network 神经网络

源码获取

本案例将介绍基础的三层神经网络，神经网络非常重要的一点便是激活函数。本次我们将使用Sigmoid函数，在前向传播时需要激活函数，而在反向传播时同样需要用到激活函数。
神经网络模型如下：

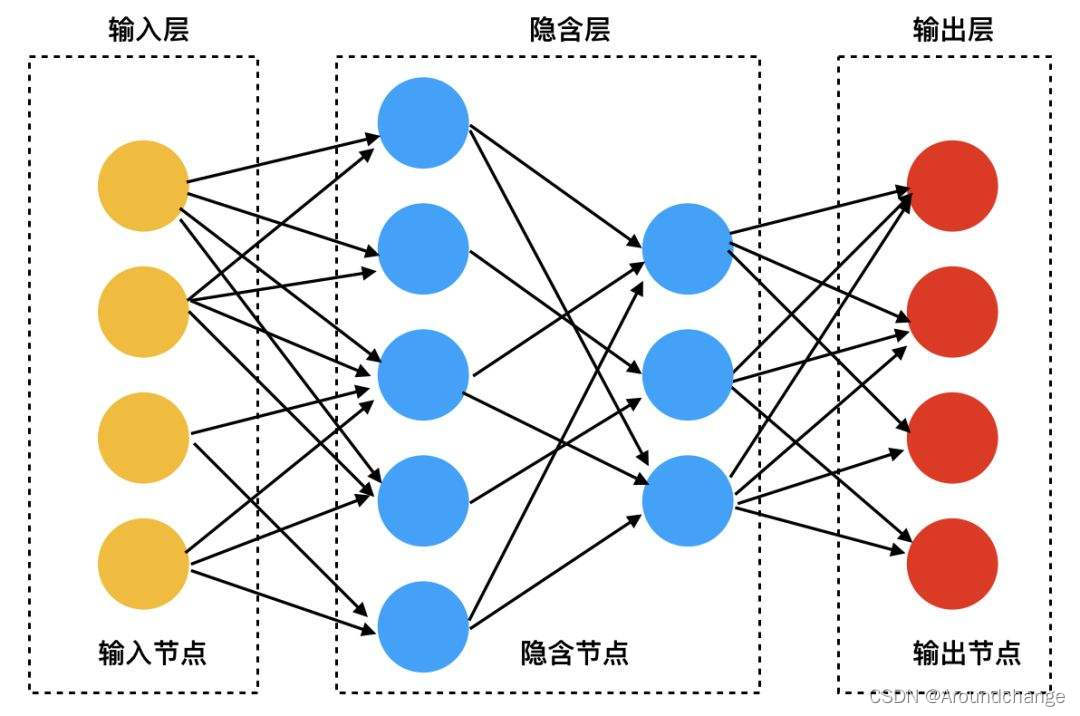
请添加图片描述

代码实现

import numpy as np


def sigmoid(x, deriv=False):
    if deriv == True:
        return x * (1 - x)
    return 1 / (1 + np.exp(-x))


x = np.array([[0, 0, 1],
              [0, 1, 1],
              [1, 0, 1],
              [1, 1, 1],
              [0, 0, 1]]
             )
# print(x.shape)

y = np.array([[0],
              [1],
              [1],
              [0],
              [0]]
             )
# print(y.shape)

np.random.seed(1)

w0 = 2 * np.random.random((3, 4)) - 1
w1 = 2 * np.random.random((4, 1)) - 1

# print(w0)

for j in range(50000):
    l0 = x
    l1 = sigmoid(np.dot(l0, w0))
    l2 = sigmoid(np.dot(l1, w1))
    l2_error = y - l2
    # print(l2_error.shape)
    if (j % 10000) == 0:
        print('Error' + str(np.mean(np.abs(l2_error))))
    l2_delta = l2_error * sigmoid(l2, deriv=True)
    # print(l2_delta.shape)
    l1_error = l2_delta.dot(w1.T)
    l1_delta = l1_error * sigmoid(l1, deriv=True)

    w1 += l1.T.dot(l2_delta)
    w0 += l0.T.dot(l1_delta)