分类：最大熵

基础概念

1、信息熵

设离散型随机变量X的取值有$x_1,x_2,...,x_n$，其发生的概率为$p_1,p_2,...,p_n$，则变量X的信息熵为：

2、条件熵

设随机变量$(X,Y)$具有联合概率分布：

则随机变量$(X,Y)$的信息熵为：

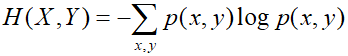
条件熵$H(Y|X)$表示在已知随机变量X的条件下随机变量Y的不确定性。定义为：

3、最大熵原理

我们设数据集为$(x_1,x_2,...,x_n)$。最大熵原理认为：在所有可能的概率模型中，熵最大的模型为最好的概率模型。求最大熵模型的步骤大致为：

1、根据已知约束条件筛选出可能的概率模型$p(y|x)$
2、在所有可能的概率模型中选出一个熵最大的模型$p(y|x)$作为最终的模型。

更多内容可以参考这篇文章，最大熵原理。

实现代码

# 最大熵分类
# 原理：根据求出的具有最大的熵的模型的条件概率p(y|x)来分别对各个类进行类别预测，
# 具有最大概率对应的类就是待预测数据的类别（标签）。
import math
from copy import deepcopy


class MEM(object):
    def __init__(self):
        # 一个字典，key为特征分布，value为对应的序号
        self.features = dict()
        # 训练数据
        self.train = []
        # 训练标签
        self.labels = []
        # 训练集长度
        self.size = 0
        # 特征权重，就是各个拉格朗日乘子的值，长度和特征分布的个数一致
        self.w = []
        # 上一次的特征权重，用于判断是否收敛
        self.last_w = []
        # 经验分布的特征期望
        self.ep = []
        # 训练样本的特征期望
        self.ep_ = []
        # GIS算法参数
        self.m = 0

    def fit(self, train, labels, max_iter=100):
        for d, label in zip(train, labels):
            for f in d:
                self.features[(label, f)] += 1
        self.init_params()

        for i in range(max_iter):
            self.ep = self.compute_ep()
            self.last_w = deepcopy(self.w)
            for t, w in enumerate(self.w):
                delta = 1.0 / self.m * math.log(self.ep_[t] / self.ep[t])
                self.w[t] += delta
                if self.if_converged():
                    break

    def init_params(self):
        self.size = len(self.train)
        self.m = max([len(case) for case in self.train])
        self.ep_ = [0.0] * len(self.features)
        for i, feature in enumerate(self.features):
            # 经验分布的特征期望
            self.ep_[i] = float(self.features[feature] / self.size)
            self.features[feature] = i
        self.w = [0.0] * len(self.features)
        self.last_w = [0.0] * len(self.features)

    # 计算模型在当前权重w下的特征期望
    def compute_ep(self):
        ep = [0.0] * len(self.features)
        for case in self.train:
            prob = self.compute_prob(case)  # 条件概率
            for feature in case:
                for weight, label in prob:
                    if (label, feature) in self.features.keys():
                        idx = self.features[(label, feature)]
                        ep[idx] += float(weight / self.size)  # ep，weight=p(y|x)
        return ep

    # 计算条件概率p(y|x)
    def compute_prob(self, case):
        weights = [(self.compute_w(case, label), label) for label in set(self.labels)]
        # 归一化因子
        Z = sum([weight for weight, label in weights])
        prob = [(weight / Z, label) for weight, label in weights]
        return prob

    # 计算特征总权重的指数
    def compute_w(self, case, label):
        weight = 0.0
        for feature in case:
            if (label, feature) in self.features.keys():
                weight += self.w[self.features[(label, feature)]]
        return math.exp(weight)

    # 判断是否收敛
    def if_converged(self):
        for w1, w2 in zip(self.last_w, self.w):
            if abs(w1 - w2) >= 0.01:
                return False
        return True

    # 预测分类
    def predict(self, test):
        assert isinstance(test, list)
        results = []
        for case in test:
            result = self.compute_prob(case.strip().split())
            result.sort(reverse=True)
            results.append(result[0][1])
            print(result)
        return results


if __name__ == '__main__':
    train = ['银行卡有余额 家人',
             '银行卡有余额 不加班 朋友',
             '银行卡有余额 开心 朋友',
             '银行卡有余额 开心 家人',
             '银行卡余额不多 开心 加班 朋友',
             '银行卡余额不多 不开心 不加班 朋友',
             '银行卡余额不多 不开心 不加班 家人',
             '银行卡余额不多 开心 加班 家人',
             '银行卡余额用尽 开心',
             '银行卡余额用尽 不开心',
             '银行卡余额用尽 不开心 家人',
             '银行卡余额用尽 不开心 加班',
             '银行卡余额用尽 不开心 加班 朋友 家人']
    labels = ['不出游', '出游', '出游', '出游', '出游', '不出游', '出游', '不出游', '不出游', '不出游', '不出游', '不出游', '不出游']
    tests = ['银行卡余额不多 开心 朋友',
             '银行卡余额用尽 开心 朋友',
             '银行卡余额用尽 不开心',
             '银行卡余额用尽',
             '涨薪 获得一万元信用额度 朋友请客']  # 训练样本中未出现的特征

    model = MEM()
    model.fit(train, labels)
    model.predict(tests)