电源电路E24系列反馈电阻计算表格

可调电源，包括DCDC、LDO电路的设计中，经常需要计算反馈电阻进行选型。为了提高效率，优化选型采购，抽空做了个表格进行快速计算。

1.一般反馈电阻电路如下。

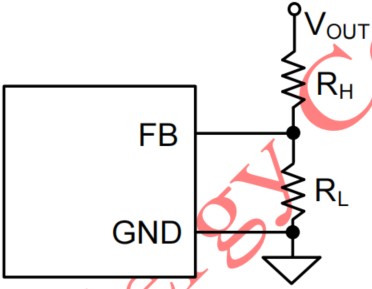
输出电压公式为：Vout=Vfb*(Rh+Rl)/Rl

2.E24电阻

标准电阻值被组织成一组称为E系列的值。E系列优选或标准电阻值范围是国际公认的，并已被国际标准组织采用。位于北美的EIA（电气工业协会）是采用该系统的一个组织，因此电阻值系列通常被称为EIA标准电阻值。因为被业界广泛应用，成本也是最优的。

E系列电阻值包括标准的E3，E6，E12，E24，E48和E96电阻值。不同数字表示相邻电阻值的公比约为10的开多少次方，例如E3电阻值公比为3√10，E6电阻值公比为6√10，等等

各个系列的电阻值列举如下。
E3标准电阻系列：1、2.2、4.7
E6标准电阻系列：1、1.5、2.2、3.3、4.7、6.8
E12标准电阻系列：1、1.2、1.5、1.8、2.2、2.7、3.3、3.9、4.7、5.6、6.8、8.2
E24标准电阻系列：1、1.1、1.2、1.3、1.5、1.6、1.8、2、2.2、2.4、2.7、3、3.3、3.6、3.9、4.3、4.7、5.1、5.6、6.2、6.8、7.5、8.2、9.1
E48和E96电阻的使用频次相对少一些，有兴趣可以自行查询电阻值列表。

3.E24计算表格

这里我们采用Excel来实现，行表示上电阻Rh，列表示下电阻Rl，并且对行标和列标进行冻结，以便于滚动查询不同组合。最终在所有单元格计算不同上下电阻值组合得到的输出电阻。为了避免干扰，对于与目标电压偏差3%以上的结果不显示，只显示出偏差±3%以内的组合计算的电压值。效果如下。

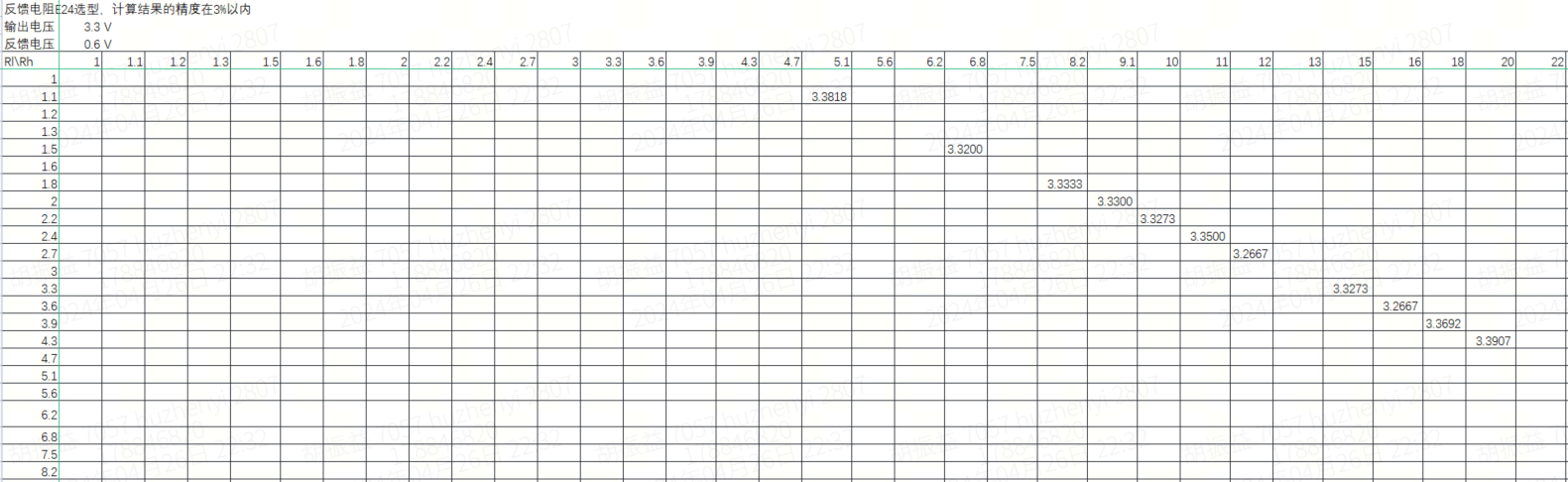
单元格只需要用一个公式来计算，第一个单元格公式如下，其他单元格拖动填充即可。
=IF(ABS($B$3(B$4+$A5)/$A5-$B$2)/$B$2<0.03,$B$3(B$4+$A5)/$A5,"")