神经元与大脑
一、神经网络
起源:试图模仿大脑的算法。
在80年代和90年代早期被广泛使用;
90年代末,流行度下降。
最近:神经网络作为最先进的技术,许多应用都在使用神经网络。
二.模型展示(一)
运用神经网络如何表示我们的假设和模型呢?
1、单个的神经元(neuron)在大脑中的样子:

神经元是一个计算单元,从输入通道接受一定数目的信息,并做些计算,然后将结果通过它的轴突传送到其他节点或者大脑中的其他神经元。
树突(Dendrite):像输入电线,接受来自其他神经元的信息。
轴突(Axon):输出通道,给其他神经元传递信号或传送信息。
2、一组神经元:
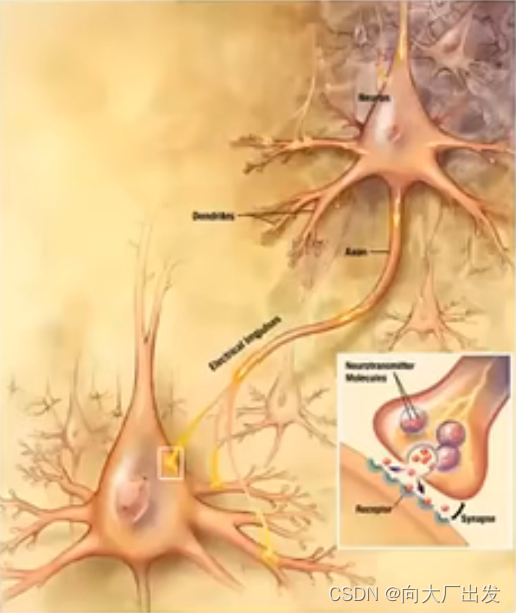
神经元之间利用微弱的电流进行沟通,也称作动作电位。
3、神经元模型:逻辑单元(Logistics unit)

x1,x2,x3代表由树突接收到的信息。
黄色圆圈代表一个神经元。


θ为模型的参数或者成为模型的权重。
x0为偏置项(有时也用b表示),值为1。
激活函数(Sigmoid(Logistic) activation funtion):非线性函数g(z)

4、Neural Network

神经网络其实就是一组神经元连接在一起的集合。
 Layer1:输入层
Layer1:输入层
Layer2:隐藏层(隐藏层的值在训练集中看不到)。在神经网络模型中可能不止一个隐藏层。
Layer3:输出层
5、


注:如不理解上述公式,可把θ看作权重放在层与层之间的连接线上,通俗易懂。

θ的上标表示第一层和第二层之间的权重矩阵,下标表示在矩阵中位置。本例中为第一个权重矩阵θ^(1)。
θ^(1)控制着从三个输入单元到三个隐藏单元的映射的权重矩阵。

一般的,如果第j层有m个单元,第(j+1)层有n个单元,则从j到(j+1)层的映射矩阵为n*(m+1).
注:此处的j层和(j+1)层的单元数不包含偏置数。
三、模型展示(二)
1、前向传播:向量化实现

2、神经网络学习自身具有的特点

3、其他神经网络架构

四、为什么神经网络可以用来学习复杂的非线性假设模型

异或(xor)是一个数学运算符。它应用于逻辑运算。异或的数学符号为“⊕”,计算机符号为“xor”。
如果两个值不相同,则异或结果为1。如果两个值相同,异或结果为0。
同或(xnor):如果两个值相同,则同或结果为1。如果两个值不相同,则同或结果为0。
五、如何利用神经网络解决多类别分类的问题
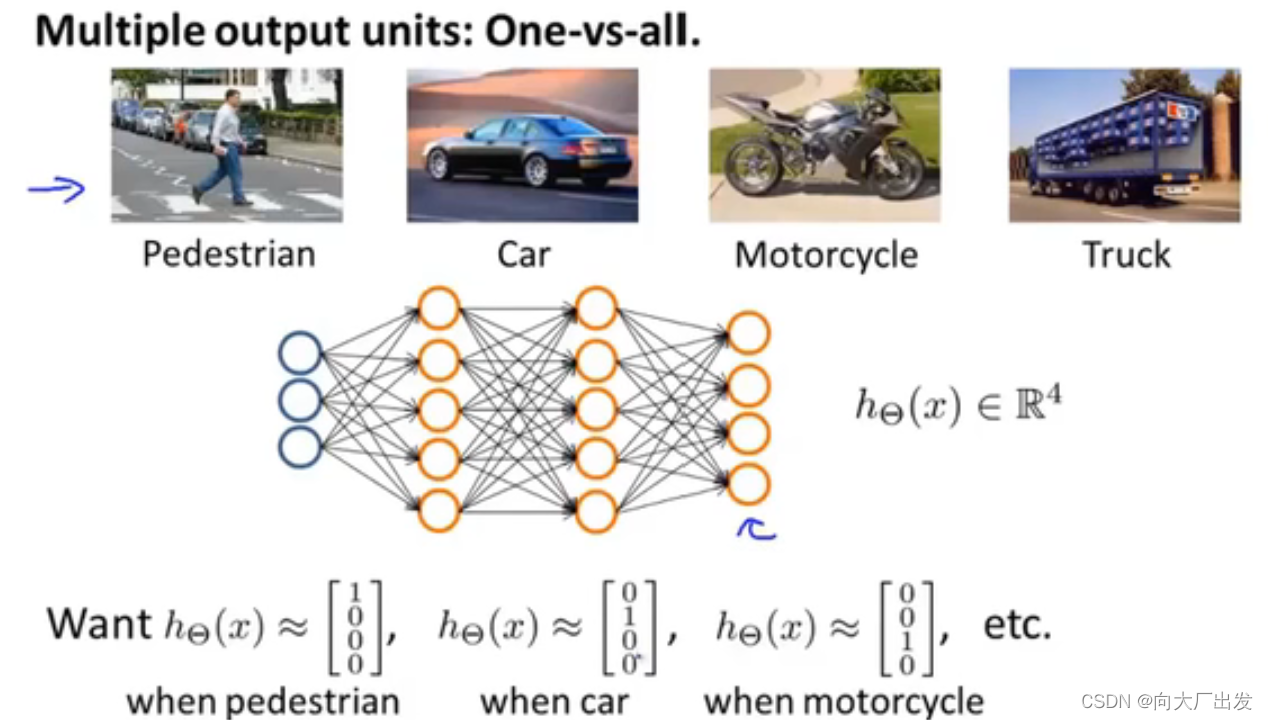























 411
411

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








