数据库原理基础：设计B树与B+树的目的以及二者的优劣

什么是B树

B树是一个满足以下条件的多叉树，一棵m阶B树满足如下条件：

• 每一个节点最多有m个子节点
• 除去叶子节点和根结点之外，其他节点至少有m/2个节点
• 包含t个子节点的节点包含有t-1个key
• 根结点如果不是叶子节点，那么至少要包含2个子结点
• 每个节点的关键字从小到大排列，每一个关键字对应的左子树都小于这个关键字，右子树都大于这个关键字
• 所有叶子节点都位于同一层

以上限定规则略显复杂，读起来可能也比较绕口，简言之就是限制每个节点的子结点个数，保证有序性以及每一个叶节点深度相同的三个特性；

B树是一种有序的数据结构，可以在log时间复杂度下完成插入、查找、删除操作；

插入操作：

自底部插入，如果满足节点个数的限制，则直接插入；如果不满足，那么一定是超出了节点个数限制，则进行调整；

调整的方式是将中间的元素插入到父节点，本身的节点分裂成两个节点（如果父节点个数也超出了继续按照这个规则调整）；

举例：如下图，插入“39”这个节点，那么第二层最左边的节点个数超出了，因此将中间的节点升为父节点，本身分裂为两个节点，最终变为第二个图的样子。

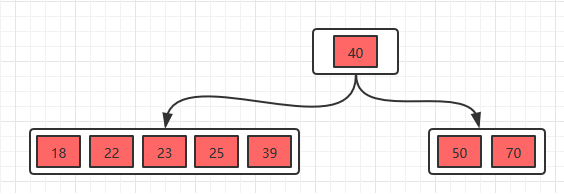
插入1

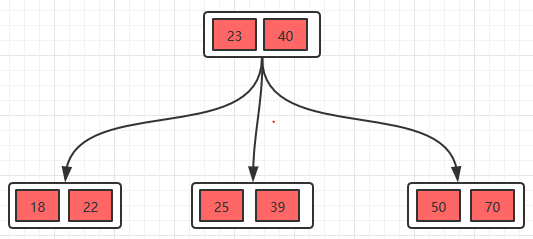
插入之后

删除操作

删除操作略微复杂，但不同情形下都是有成熟的规则的，只要按照规则来就可以；（类似于拧魔方）

1. 删除叶节点，并且删除之后 节点的key的个数满足多叉树要求，那么直接删除

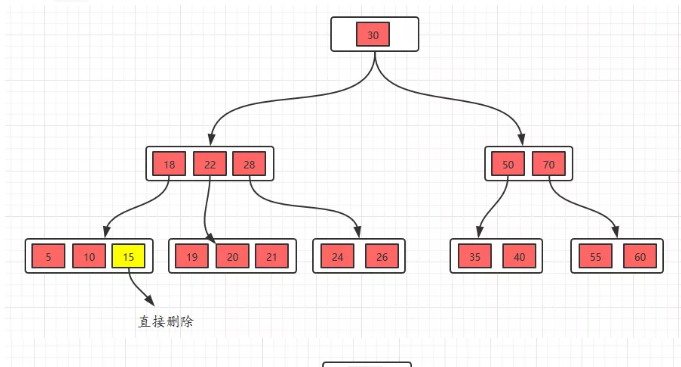
case 1

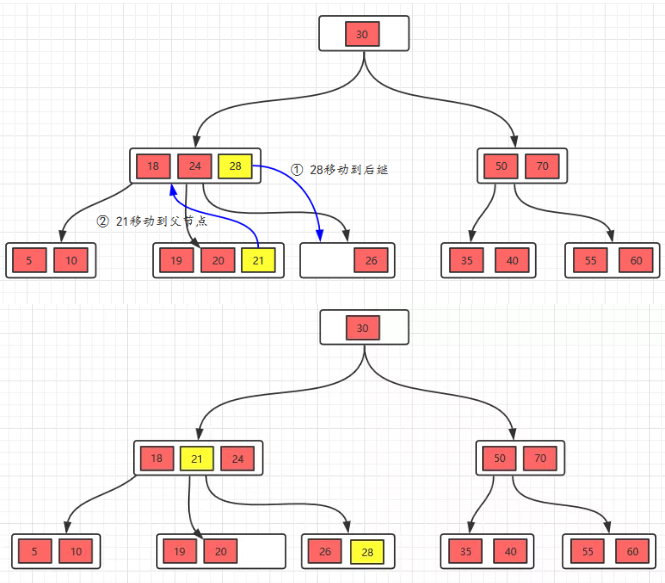
1. 删除叶节点，并且删除后不满足要求，则首先看前面的兄弟节点是否有>m/2个节点，如果>m/2个节点，那么就“借”一个，但这里并不是直接去借兄弟节点元素，是借父亲的元素，然后用兄弟节点元素来填补借的父元素。

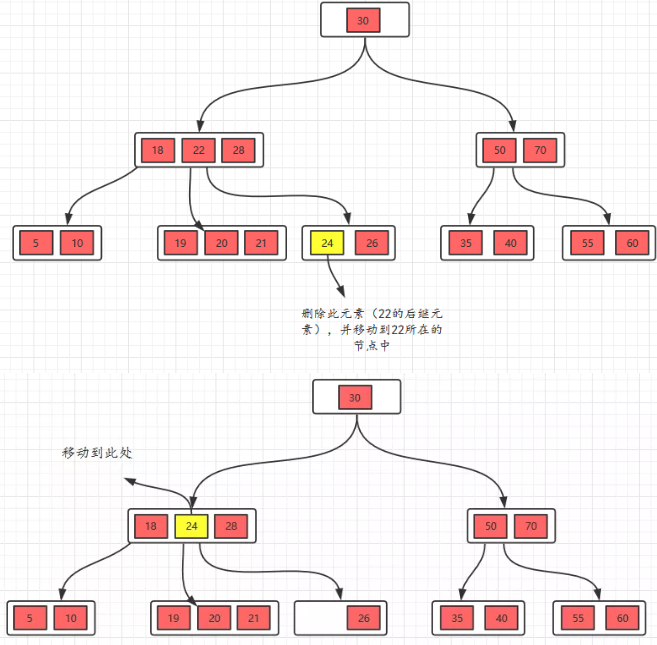
删除元素22

1. 如果删除之后，兄弟节点个数不大于m/2, 那么将父亲节点移到被删除元素的节点，然后跟兄弟节点合并；

1. 删除非叶子节点，则用此节点的右子树第一个节点来填补，同时删除右子树的第一个节点

B+树

B+树是对B树的升级，主要改动如下：

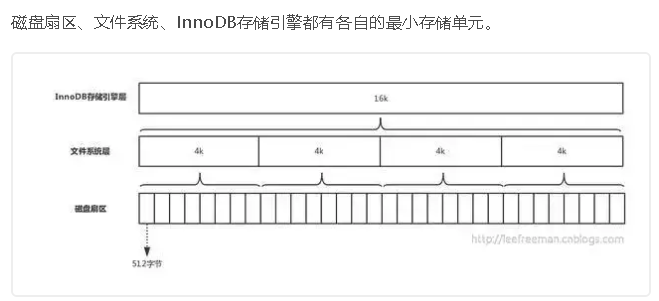
• 内部节点只存储索引，不存储数据；（这里类比聚簇索引和非聚簇索引就很明确了），对于B树来说，索引和数据会放在磁盘的同一个扇区中（或者是文件系统的同一个页中），而B+树不会；

存储划分

page=3的页中只存在索引，而数据存在其他页中；

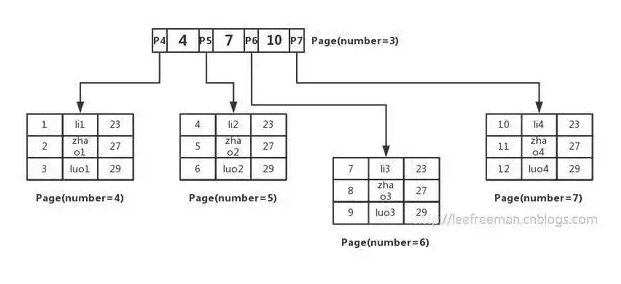
• 每一个叶子节点，都存有相邻叶节点的指针（双向链表）

采用双向链表的原因是为了方便处理"小于"的条件查询。

对比

B树和B+树都是多路查找树，目的都是为了解决多次访问磁盘，IO耗时太长的问题；

如果采用二叉树，虽然查找的时间复杂度没变，但是由于每一个节点可能在不同的页上，因此访问磁盘的次数增多。

B+树进一步优化了磁盘访问次数，将索引和数据分开存储，因此每一个页中存储的索引更多。

B+树的叶节点增加了指针链接，可以查询效率更高；

但同样的，B+树对查询的优化操作会降低了一定写入性能。