LeetCode刷题之HOT100之二叉树的最近公共祖先

2024 7/1 新的一个月来啦！也算是迎来了暑假，可惜我们没有暑假，只能待实验室，中途会有10天小假。Anyway，做题啦

1、题目描述

2、算法分析

又来到了树的部分，要找最近的公共祖先。想到树就会想到DFS和BFS。
祖先的定义： 若节点 p 在节点 root 的左（右）子树中，或 p=root ，则称 root 是 p 的祖先。这与人类社会关系唯一不同的是，自己也可以是自己的祖先。
最近公共祖先的定义： 设节点 root 为节点 p,q 的某公共祖先，若其左子节点 root.left 和右子节点 root.right 都不是 p,q 的公共祖先，则称 root 是 “最近的公共祖先” 。
这里使用递归方式，利用DFS算法。那么符合条件的最近公共祖先 一定满足如下条件：

((leftSon && rightSon) || ((root.val == p.val || root.val == q.val) && (leftSon || rightSon)))

如果 p 和 q 分别在左右子树中，或者 p 和 q 中的一个等于当前节点并且 p 和 q 在子树中，则当前节点为最近公共祖先

3、代码

 // 定义一个私有成员变量res，用于存储找到的最低公共祖先节点
    private TreeNode res;
    // 构造函数，初始化res为null
    public Solution(){
        this.res = null;
    }
    // 定义一个私有递归方法dfs，用于在二叉树中查找最低公共祖先  
    // 参数：  
    //   root - 当前遍历的节点  
    //   p - 给定的节点p  
    //   q - 给定的节点q  
    // 返回值：  
    //   一个布尔值，表示p和q是否都在当前子树中
    private boolean dfs(TreeNode root, TreeNode p, TreeNode q){
        // 如果当前节点为空，说明已经遍历到叶子节点的下方，返回false 
        if(root == null ){
            return false;
        }
        // 递归地在左子树中查找p和q 
        boolean leftSon = dfs(root.left, p, q);
        // 递归地在右子树中查找p和q
        boolean rightSon = dfs(root.right, p, q);
        // 如果 p 和 q 分别在左右子树中，或者 p 和 q 中的一个等于当前节点并且 p 和 q 在子树中，则当前节点为最近公共祖先
        if((leftSon && rightSon) || ((root.val == p.val || root.val == q.val) && (leftSon || rightSon))){
            res = root;
        }
        // 返回p和q是否在当前子树中（包括当前节点）
        return leftSon || rightSon || (root.val == p.val || root.val == q.val);
    }
    // 公开方法，用于调用私有方法dfs并返回找到的最低公共祖先节点 
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        // 调用dfs方法
        this.dfs(root, p, q);
        // 返回找到的最低公共祖先节点
        return this.res;   
    }

我们举一个例子来说明：如下图所示，我们要找7和8的最近公共祖先。

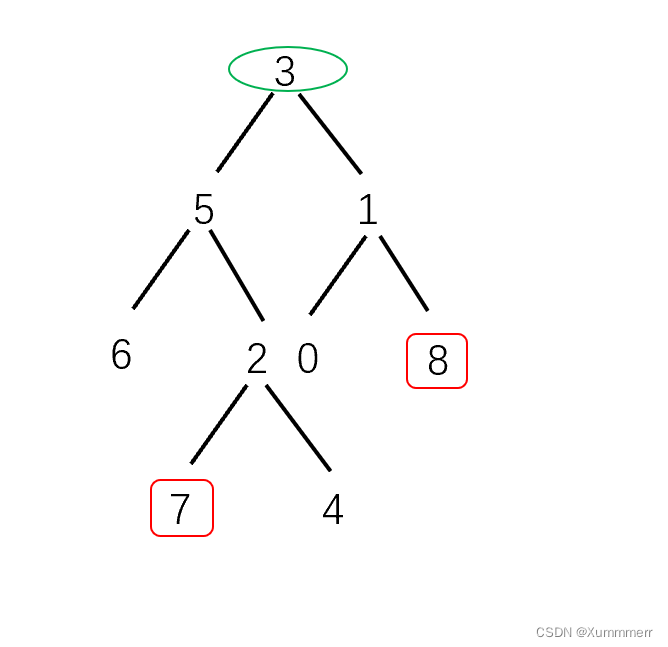
以下是调用lowestCommonAncestor方法并找到LCA的步骤：

• 从根节点3开始调用dfs方法，并将7和8作为要查找的节点。
• dfs方法首先检查当前节点3，然后递归地在其左子树（以5为根）中查找7和8。
• 在左子树中，dfs方法会首先检查节点5，然后递归地在节点5的左子树（以6为根）中查找7和8。由于节点6没有子节点，所以dfs(6, 7,8)返回false，表示7和8都不在节点6的子树中。
• 接着，dfs方法会检查节点5的右子树（以2为根）。在右子树中，它发现节点7是2的右子节点，所以dfs(2, 7,8)返回true，因为节点7在节点2的子树中。
• 此时，dfs方法回到节点5，并发现leftSon为false（因为7不在左子树中），而rightSon为true（因为7在右子树中）。但是，因为7和8没有同时在左右子树中，所以节点5不是7和8的LCA。
• dfs方法返回true到根节点3，表示7在节点3的左子树中。
• 接下来，dfs方法检查根节点3的右子树（以1为根）。在右子树中，它发现节点8是1的右子节点，所以dfs(1, 7, 8)返回true，因为节点8在节点1的子树中。
• 此时，dfs方法再次回到根节点3，并发现leftSon和rightSon都为true（因为7在左子树中，8在右子树中）。根据条件(leftSon&& rightSon)，节点3被确定为7和8的LCA，并将res设置为节点3。
• 最后，lowestCommonAncestor方法返回存储在res中的节点，即节点3。
  因此，节点7和8的LCA是节点3。

4、复杂度分析

• 时间复杂度：O(N)，其中 N 是二叉树的节点数。二叉树的所有节点有且只会被访问一次，因此时间复杂度为 O(N)。
• 空间复杂度：O(N) ，其中 N 是二叉树的节点数。递归调用的栈深度取决于二叉树的高度，二叉树最坏情况下为一条链，此时高度为 N，因此空间复杂度为 O(N)。

ok啦，做完啦，拜拜！