数据处理+贪婪算法+主成分分析PCA+线性判别分析 (LDA)+Fisher 判别准则

异常值与重复数据检测

局部离群因子 (Local Outlier Factor, LOF) 算法

LOF算法是一种用于检测数据集中异常点的算法。其核心思想是比较一个点的局部密度与其邻居的局部密度。算法的主要步骤和公式如下：

1. 计算k-距离（k-distance）:
   对于每个点P，其k-距离被定义为点P和它的第k个最近邻居之间的距离。

2. 计算可达距离（Reachability Distance）:
   可达距离定义为点A到点B的距离与点B的k-距离的最大值。
   $${\text{Reachability-Distance}}_k(A,B)=\max (\text{k-distance}(B),d(A,B))$$
   其中d(A, B)是点A和点B之间的距离。

3. 计算局部可达密度（Local Reachability Density, LRD）:
   点P的局部可达密度是点P的k个最近邻居的可达距离的倒数的平均值。
   $${\text{LRD}}_k(P)=\frac{1}{\frac{{\sum }_{O\in N_k(P)}{\text{Reachability-Distance}}_k(P,O)}{|N_k(P)|}}$$
   其中N_k(P)是点P的k个最近邻居。

4. 计算局部离群因子（LOF）:
   对于每个点P，其局部离群因子是其邻居的局部可达密度与它自己的局部可达密度的比值的平均值。
   $${\text{LOF}}_k(P)=\frac{{\sum }_{O\in N_k(P)}\frac{{\text{LRD}}_k(O)}{{\text{LRD}}_k(P)}}{|N_k(P)|}$$

数据描述

数据最好用中位数median，而不是均值mean
mode众数
mean平均值

方差variance:
$$\text{Var}(X)=\frac{1}{N}\sum _{i=1}^N(x_i-\mu {)}^2$$

皮尔森积差相关系数
$$R(A，B)=\frac{{\sum }_{i=1}^N(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{{\sum }_{i=1}^N(x_i-\overline{x}{)}^2{\sum }_{i=1}^N(y_i-\overline{y}{)}^2}}$$

如果R(A，B)>0，则A和B正相关。
如果R(A，B)=0，则A和B之间没有线性相关性。只是没有线性不相关，可能有其他相关性。
若R(A，B)<0，则A与B呈负相关。

卡方检验：
$${\chi }^2=\sum \frac{(O_i-E_i{)}^2}{E_i}其中O_i是观察值,E_i是期望值。$$

简单的贪婪算法

用于从数据集中选择最重要的 K 个特征
用于减小数据集的维度，或者为了找出影响目标变量最多的特征。

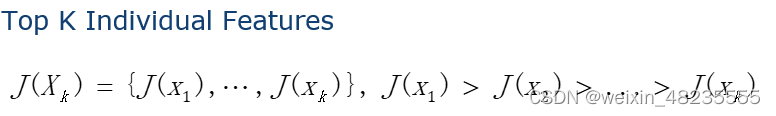
1. 顺序前进法（sequential forward selection，SFS）
   从零个特征开始，逐步添加最有价值的特征，直到特征数量达到预定的 K 个。在每一步，它都会考虑添加剩下的特征中对当前选中的特征集合增益最大的一个。
   算法步骤：
2. 开始时，选定的特征集合为空。
3. 对于每个未被选定的特征，评估将该特征添加到当前特征集合中后的模型性能。
4. 选择使得模型性能提升最大的特征，并将其加入到特征集合中。
5. 重复步骤 2 和 3，直到达到预定的特征数量 K。
   

from mlxtend.feature_selection import SequentialFeatureSelector as SFS
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris

# 载入数据
iris = load_iris()
X = iris.data
y = iris.target

# K-近邻分类器
knn = KNeighborsClassifier(n_neighbors=3)

# 顺序前进法
sfs = SFS(knn, 
          k_features=3, 
          forward=True, 
          floating=False, 
          scoring='accuracy',
          cv=5)

# 进行特征选择
sfs = sfs.fit(X, y)

# 输出选定的特征
print('Selected features:', sfs.k_feature_idx_)

2. 顺序后向选择（Sequential Backward Selection，SBS）
   它从所有特征开始，逐步移除最不重要的特征，直到剩下 K 个特征。在每一步，它都会考虑移除当前选中的特征集合中最不重要的一个。

算法步骤：

1. 开始时，选定的特征集合包含所有特征。
2. 对于每个已被选定的特征，评估从当前特征集合中移除该特征后的模型性能。
3. 移除使得模型性能损失最小的特征。
4. 重复步骤 2 和 3，直到特征集合中只剩下 K 个特征。

from mlxtend.feature_selection import SequentialFeatureSelector as SFS
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris

# 载入鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target

# 创建 K-近邻分类器实例
knn = KNeighborsClassifier(n_neighbors=3)

# 顺序后向选择
sbs = SFS(knn, 
          k_features=3,  # 指定选择的特征数量
          forward=False,  # 设置为后向选择
          floating=False, 
          scoring='accuracy',  # 使用准确度作为评估指标
          cv=5)  # 使用5折交叉验证

# 对数据集进行特征选择
sbs = sbs.fit(X, y)

# 打印选择的特征索引
print('Selected features:', sbs.k_feature_idx_)

主成分分析PCA

主成分分析（Principal Component Analysis，简称 PCA）是一种常用的数据降维技术，它通过线性变换将原始数据转换成一组各维度线性无关的表示，称为主成分。PCA 主要用于提取数据中的关键特征，降低数据维度，同时尽量保留原始数据的信息。

基本原理

PCA 通过寻找一个新的坐标系统，使得在这个新坐标系下，数据的方差最大化。在新坐标系下，第一个坐标（称为第一主成分）是原始数据方差最大的方向，第二个坐标（第二主成分）是与第一主成分正交且方差次大的方向，依此类推。这些主成分作为新的特征集，可以捕捉到数据中最重要的变异性。

基本步骤

1. 数据标准化

   将数据进行中心化处理，使得每个特征的均值为0，即对于每个特征 $x_i$，进行转换 $x_i^{\prime }=x_i-\overline{x_i}$，其中 $\overline{x_i}$ 是特征 $x_i$ 的均值。

2. 计算协方差矩阵

   协方差矩阵 $C$ 可以表示为：

   $$C=\frac{1}{n-1}\times X^{T}X$$

   其中，$X$ 是标准化后的数据矩阵，$n$ 是样本数。

3. 计算协方差矩阵的特征值和特征向量

   特征值和特征向量描述了数据的主要变化方向。特征向量 $v$ 和对应的特征值 $\lambda$ 满足：

   $$Cv=\lambda v$$

4. 选择主成分

   选择 $k$ 个最大的特征值对应的特征向量，形成一个转换矩阵 $W$。

5. 将数据转换到新的低维空间

   使用转换矩阵 $W$ 将原始数据 $X$ 映射到新的低维空间：

   $$Y=XW$$

   这里，$Y$ 是映射后的低维数据。

应用

PCA 常用于特征提取、数据压缩、可视化等。它帮助去除数据中的冗余特征，同时保留最重要的信息。

线性判别分析 (LDA)

线性判别分析（Linear Discriminant Analysis，简称 LDA）是一种在统计学、模式识别和机器学习中用于分类和降维的方法。LDA 旨在找到一个线性组合的特征，使得不同类别的数据最大程度上可分。

基本原理

LDA 的主要思想是寻找一个线性投影，该投影能够将不同类别的样本投射到不同的位置，以最大化类间距离和最小化类内距离。

数学描述

假设有 $n$ 维特征空间中的两个类别，每个类别中有多个样本。LDA 的目标是找到一个方向向量 $w$，使得将所有样本投射到这个方向上后，类间方差最大，而类内方差最小。

1. 计算类内散度矩阵 $S_W$ 和 类间散度矩阵 $S_B$：

   类内散度矩阵 $S_W$ 是各个类别内部样本与各自类别均值的离差平方和：

   $$S_W=\sum _{i=1}^c\sum _{x\in D_i}(x-{\mu }_i)(x-{\mu }_i{)}^T$$

   其中，$c$ 是类别数，$D_i$ 是第 $i$ 个类别的样本集，${\mu }_i$ 是第 $i$ 个类别的均值向量。

   类间散度矩阵 $S_B$ 是不同类别的均值与总体均值的离差平方和：

   $$S_B=\sum _{i=1}^c{n}_i({\mu }_i-\mu )({\mu }_i-\mu {)}^T$$

   其中，$n_i$ 是第 $i$ 个类别的样本数，$\mu$ 是总体均值向量。

2. 计算投影方向：

   LDA 的目标是最大化类间散度矩阵和类内散度矩阵的比例。因此，求解的方向向量 $w$ 满足：

   $$w=\arg \max \frac{w^T{S}_{B}w}{w^T{S}_{W}w}$$

   这个问题可以通过求解广义特征值问题来解决：

   $$S_{B}w=\lambda S_{W}w$$

3. 数据投影：

   通过计算得到的最优投影方向 $w$，可以将原始数据投影到新的低维空间：

   $$y=w^{T}x$$

   其中，$x$ 是原始数据点，$y$ 是投影后的数据点。

应用

LDA 常用于特征降维、分类等领域。它能够提取对分类最有用的特征，并在新的低维空间中保持类别之间的最大可分性。

Fisher Criterion（Fisher 判别准则）

Fisher Criterion，或称 Fisher 判别准则，是一种度量线性判别分析（LDA）中类别可分性的标准。它由统计学家和生物学家 Ronald Fisher 提出，主要用于分类任务中的特征选择和降维。

基本原理

Fisher 判别准则的基本思想是找到一个方向，使得在该方向上投影后，不同类别的数据最大程度地分离。具体来说，它旨在最大化类间距离，同时最小化类内差异。

数学描述

假设有两个类别，各自有多个样本，Fisher 判别准则的目标是找到一个方向向量 $w$，在这个方向上，两个类别的数据尽可能分开。

1. 类内散度矩阵 $S_W$ 和 类间散度矩阵 $S_B$：

   类内散度矩阵 $S_W$ 表示各个类别内部样本的离差平方和：

   $$S_W=\sum _{i=1}^c\sum _{x\in D_i}(x-{\mu }_i)(x-{\mu }_i{)}^T$$

   类间散度矩阵 $S_B$ 表示不同类别的均值与总体均值的离差平方和：

   $$S_B=\sum _{i=1}^c{n}_i({\mu }_i-\mu )({\mu }_i-\mu {)}^T$$

2. Fisher 判别准则：

   Fisher 判别准则通过最大化下面的比值来找到最优的投影方向 $w$：

   $$J(w)=\frac{w^T{S}_{B}w}{w^T{S}_{W}w}$$

   目标是最大化 $J(w)$，即最大化类间距离和最小化类内差异。

3. 求解投影方向：

   通过求解广义特征值问题来找到最优的 $w$：

   $$S_{B}w=\lambda S_{W}w$$

4. 数据投影：

   使用计算得到的 $w$，将原始数据投影到新的方向：

   $$y=w^{T}x$$

   这里，$x$ 是原始数据点，$y$ 是投影后的数据点。

应用

Fisher 判别准则在特征选择、降维和模式识别等领域中有广泛应用。通过这种方式，可以有效地提取特征，使得分类任务的效果得到显著提升。