【论文阅读】FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness

Abstract

Transformer模型在处理长序列时速度缓慢且内存消耗巨大，这是由于自注意力机制的时间和内存复杂度与序列长度呈平方关系。近似注意力方法尝试通过牺牲模型质量来降低计算复杂度，以应对这一问题，但通常并不能达到实际运行时间上的加速。作者认为缺失的一个关键原则是：使注意力算法具备 IO 感知能力 —— 即考虑 GPU 内存各层级之间的读写开销。作者提出了FlashAttention，这是一种具备 IO 感知的精确注意力算法，它通过切分技术来减少 GPU 高带宽内存（HBM）与 GPU 片上 SRAM 之间的内存读写次数。作者分析了 FlashAttention 的 IO 复杂度，结果表明其比标准注意力机制需要更少的 HBM 访问次数，并且在一系列 SRAM 容量下都能达到最优性能。作者还将 FlashAttention 扩展到了块稀疏注意力，由此产生了一种比现有任何近似注意力方法都更快的近似注意力算法。FlashAttention 能够让 Transformer 的训练速度超过现有基线：在 BERT-large（序列长度512）上，相比 MLPerf 1.1 训练速度纪录，实现了15% 的端到端实际运行时间加速；在 GPT-2（序列长度1K）上实现了3倍加速；在 Long-Range Arena（序列长度1K-4K）上实现了2.4倍加速。FlashAttention 和块稀疏 FlashAttention 不仅使 Transformer 能够处理更长的上下文，还显著提升了模型质量（在 GPT-2 上困惑度降低 0.7，在长文档分类任务上提升 6.4 个百分点），并实现了全新的能力：首次有 Transformer 模型在 Path-X 挑战（序列长度 16K，准确率 61.4%）和 Path-256 挑战（序列长度 64K，准确率 63.1%）上超越随机猜测表现。

1 Introduction

Transformer 模型 [82] 已成为自然语言处理和图像分类等应用中最广泛使用的架构。尽管 Transformer 规模越来越大 [5]、网络层数越来越深 [83]，但由于其核心的自注意力模块在时间和内存上的复杂度都随着序列长度呈平方关系，为其配备更长上下文的能力仍然面临挑战 [80]。一个重要的问题在于：若能提升注意力机制的速度和内存效率，是否可以帮助 Transformer 模型应对长序列下的运行时间和内存瓶颈。

当前已有多种近似注意力方法试图降低注意力机制的计算和内存需求。这些方法涵盖了从稀疏近似 [51，74] 到低秩近似 [12，50，84]，以及两者的组合方案 [3，9，92]。尽管这些方法将计算需求降低到与序列长度呈线性或近似线性关系，但其中多数方案相比标准注意力机制并未展现出实际运行速度的优势，因而未能获得广泛应用。一个主要原因是这些方法关注浮点运算量（FLOPs）的削减，这与实际运行速度未必正相关，同时它们普遍忽视了内存访问（IO）带来的额外开销。

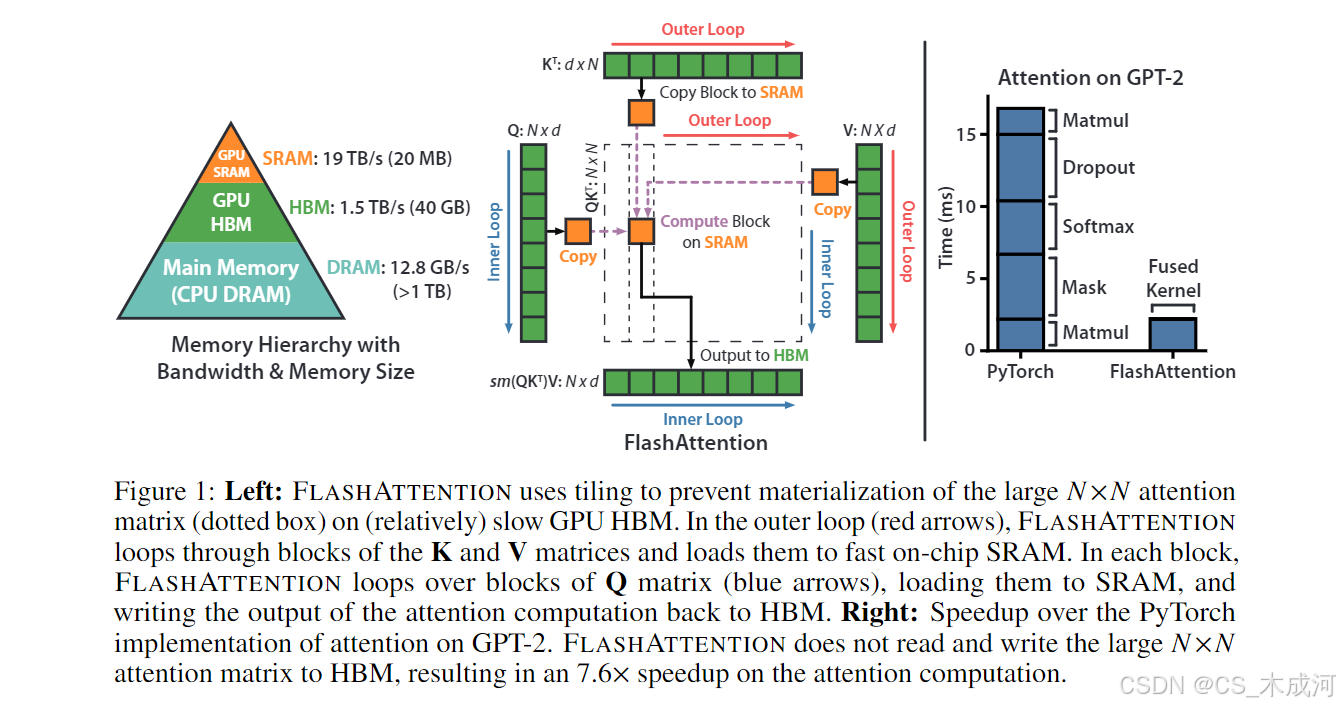
在本文中，作者指出一个缺失的原则是让注意力算法具备 IO 感知能力[1] —— 即需要精确考量在不同层级的快速与慢速内存之间的读写开销（例如快速的 GPU 片上 SRAM 与相对较慢的 GPU 高带宽内存 HBM [45]，见图1左）。在现代 GPU 架构中，计算速度已经远远超过了内存访问速度 [61，62，63]，因此 Transformer 中大多数操作都受限于内存访问带宽[43]。对于这类内存受限的操作，当数据读写占运行时长的绝大部分时（如数据库连接[71]、图像处理[70]、数值线性代数[4]等场景[40,85]），IO 感知算法是至关重要的。然而，像 PyTorch 和 TensorFlow 这样的主流深度学习框架的 Python 接口并不支持对内存访问进行细粒度的控制。

作者提出了一种全新的注意力算法 FlashAttention，该算法能以大幅减少的内存访问来计算精确注意力。作者的核心目标是避免注意力矩阵频繁读写到 HBM。这需要 (i)在无法访问整个输入的情况下完成 softmax 归一化的计算；(ii)无需存储庞大的中间注意力矩阵以供反向传播。为此，作者采用了两种成熟的技术来解决上述问题：(i)通过重构注意力计算流程，将输入切分为多个块，并对这些输入块进行多次遍历，从而逐步进行 softmax 的归一化计算（也称为 tiling）；(ii)在前向传播时存储 softmax 归一化因子，使得反向传播时能在片上快速重新计算注意力，这比从 HBM 读取中间注意力矩阵的标准方法更为高效。作者在 CUDA 中实现了 FlashAttention，以达到对内存访问的细粒度控制，并将所有注意力操作融合至单个 GPU 内核中。尽管由于重计算导致浮点运算量（FLOPs）有所增加，但得益于 HBM 访问量的大幅降低，作者的算法比标准注意力运行得更快（在 GPT-2 [67] 上最高可达 7.6 倍加速，见图1右），同时内存占用更少，降至序列长度的线性复杂度。

作者分析了 FlashAttention 的 IO 复杂度[1]，证明其需要 $O(N^2{d}^2{M}^{-1})$ 次 HBM 访问，其中 $d$ 为头维度，$M$为 SRAM 容量，相比于标准注意力的 $\Omega (Nd+N^2)$次 HBM 访问。在 $d$ 和 $M$ 的典型值下，FlashAttention 所需的 HBM 访问次数比标准注意力少了数倍（最高达9倍，如图2所示）。此外，作者给出了理论下界：在所有 SRAM 容量下，任何精确注意力算法在 HBM 访问次数上均无法渐近优于该结果。

作者还证明，FlashAttention 可通过克服内存访问开销问题，成为一种实现近似注意力算法潜力的有用基础算子。作为概念验证，作者实现了块稀疏FlashAttention——该稀疏注意力算法比标准FlashAttention快2-4倍，并能够扩展到64k的序列。作者证明块稀疏FlashAttention的IO复杂度优于标准FlashAttention，其提升比例与稀疏率成正比。作者在第5节中讨论其他操作（多GPU上的注意力计算，核回归以及块稀疏矩阵乘法）的进一步拓展。作者开源了 FlashAttention，以更容易在此基础上构建。

作者通过实证验证，FlashAttention能够通过建模更长上下文来加速模型训练并提升模型质量。同时，作者对FlashAttention及块稀疏FlashAttention的运行时间和内存占用进行了基准测试，并与先前的注意力实现进行了对比。

• 更快的模型训练。FlashAttention 能在实际时间上更快地训练 Transformer 模型。作者在 BERT-large（序列长度 512）训练中，比 MLPerf 1.1 [58] 的训练速度纪录快了 15%；在 GPT-2（序列长度 1K）训练中，比 HuggingFace [87] 和 Megatron-LM [77] 的基线实现快了 3 倍；在 Long-Range Arena（序列长度 1K–4K）任务中，比基线快了 2.4 倍。

• 更高质量的模型。FlashAttention 使 Transformer 能够扩展到更长的序列，从而提升模型质量并实现新的能力。作者观察到，在 GPT-2 上困惑度提升了 0.7；在长文档分类任务 [13] 上，通过建模更长的序列，准确率提升了 6.4 个百分点。FlashAttention 使 Transformer 首次仅通过使用更长的序列长度（16K），就能在 Path-X [80] 挑战中取得了优于随机基准的表现。块稀疏 FlashAttention 将 Transformer 扩展到 64K 的超长序列，并首次在 Path-256 挑战上取得优于随机基准的表现。

• 注意力机制基准测试。FlashAttention 在常见的序列长度（128 到 2K）上，比标准注意力实现快达 3 倍，并能够扩展到 64K 的序列长度。在 512 的序列长度内，FlashAttention 在速度和内存效率上均优于所有现有的注意力方法。当序列长度超过 1K 时，某些近似注意力方法（如 Linformer）开始变得比 FlashAttention 更快。但是，块稀疏 FlashAttention 比已知的所有现有近似注意力方法都快。

2 Background

作者提供一些现代硬件（GPU）上常见深度学习操作的性能特征的背景，并描述注意力的标准实现。

2.1 Hardware Performance

作者在此主要关注 GPU，其他硬件加速器上的性能表现也具有类似的特征 [46，48]。

GPU 内存层级结构。GPU 的内存层级（见图 1 左）由不同规模和速度的多种内存形式组成，内存规模越小速度越快。以 A100 GPU 为例，其配备有40–80GB 的高带宽内存（HBM），带宽为 1.5–2.0TB/s；108 个流式多处理器中的每一个都有 192KB 的片上 SRAM，带宽约为 19TB/s [44，45]。片上 SRAM 的带宽比 HBM 快一个数量级，但规模小几个数量级。随着计算相对于内存速度变得更快[61,62,63]，操作越来越受到内存（HBM）访问的瓶颈。因此有效利用高速的 SRAM 变得尤为重要。

执行模型。GPU 拥有大量的线程来执行操作（称为内核）。每个内核将输入从 HBM 加载到寄存器和 SRAM，进行计算，然后将输出写入 HBM。

性能特征。根据计算和内存访问的平衡，操作可以分为计算受限或内存受限。这通常通过算术强度[85]来衡量，即每字节内存访问所执行的算术操作数量。

1. 计算受限：操作所花费的时间由算术运算的数量决定，而访问 HBM 的时间则小得多。典型的示例是内维度较大的矩阵乘法和通道数较多的卷积。

2. 内存受限：操作所花费的时间由内存访问次数决定，而在计算中花费的时间要小得多。示例包括大多数其他操作：逐元素操作（如激活函数、dropout）与规约操作（如求和、softmax、批归一化、层归一化）。

核融合。加速内存受限操作的最常见方法是核融合：如果有多个操作作用于相同的输入，则可以将输入从 HBM 中只加载一次，而不是为每个操作多次加载。编译器可以自动融合许多逐元素操作[53,65,75]。然而，在模型训练的背景下，中间值仍然需要写入 HBM 以便用于反向传播，从而降低了简单核融合的效率。

2.2 Standard Attention Implementation

给定输入序列 $\mathbf{Q},\mathbf{K},\mathbf{V}\in {\mathbb{R}}^{N\times d}$，其中 $N$ 是序列长度，$d$ 是头维度，作者想计算注意力输出 $\mathbf{O}\in {\mathbb{R}}^{N\times d}$：

$$\mathbf{S}=\mathbf{Q}{\mathbf{K}}^{\top }\in {\mathbb{R}}^{N\times N},\mathbf{P}=\mathrm{softmax}(\mathbf{S})\in {\mathbb{R}}^{N\times N},\mathbf{O}=\mathbf{PV}\in {\mathbb{R}}^{N\times d},$$

其中 softmax 按行使用。

标准的注意力实现会将矩阵 $\mathbf{S}$ 和 $\mathbf{P}$ 完整地存至 HBM，这消耗 $O(N^2)$ 的内存。通常 $N\gg d$（例如 GPT2 中，$N=1024$，$d=64$）。作者在Algorithm 0 中描述标准注意力实现的流程。由于一些或大多数操作是内存受限的（例如softmax），大量内存访问将导致实际运行时间延长。

该问题会因注意力矩阵的其他逐元素操作而加剧，例如对 $\mathbf{S}$ 的 masking 或对 $\mathbf{P}$ 的 dropout。因此，已经有许多研究尝试去融合多个逐元素操作，例如将masking 与 softmax 融合[77]。

在第 3.2 节中，作者将展示标准注意力实现在 HBM 上的访问次数与序列长度 $N$ 呈平方关系。作者还将对比标准注意力与本文方法（FlashAttention）的浮点运算量（FLOPs）及 HBM 访问次数。

3 FlashAttention: Algorithm, Analysis, and Extensions

作者证明了如何在不读取/写入大量 HBM 以及不存储大规模中间矩阵以供反向传播的情况下，计算精确注意力。这产生了一种内存使用高效且实际运行时间更快的注意力算法。作者分析了该算法的 IO 复杂度，并证明与标准注意力相比，作者的方法需要更少的 HBM 访问。作者进一步证明，FlashAttention 可以通过扩展它去处理块稀疏注意力，来作为一种通用基础组件。

为了便于说明，作者在这主要关注前向传播；关于反向传播的详细内容请参见附录 B。

3.1 An Efficient Attention Algorithm With Tiling and Recomputation

给定 HBM 中的输入 $\mathbf{Q},\mathbf{K},\mathbf{V}\in {\mathbb{R}}^{N\times d}$，目标是计算注意力输出 $\mathbf{O}\in {\mathbb{R}}^{N\times d}$ 并将其写入 HBM。作者的目标是减少 HBM 访问次数（减至与 $N$ 成亚二次关系的数量级）。

作者采用两种已有的技术（分块、重计算）来应对在亚二次数量级的 HBM 访问情况下计算精确注意力所面临的技术挑战。作者在算法 1 中对此进行了阐述。其主要思路是，将输入的 $\mathbf{Q},\mathbf{K},\mathbf{V}$ 分割成多个块，将它们从慢速的 HBM 加载到快速的 SRAM 中，然后针对这些块计算注意力的输出。在将每个块的输出相加之前，通过乘以合适的归一化因子来对其进行缩放，最终就能得到正确的结果。

分块技术。根据块来计算注意力。softmax 会耦合 $\mathbf{K}$ 的列，因此通过缩放对大规模的 softmax 进行分解[51，60，66]。为了保证数值稳定性，向量 $\mathbf{x}\in {\mathbb{R}}^B$ 的 softmax 计算方式为：

$$m(x):=\underset{i}{\max }{x}_i,f(x):=\left[e^{x_1-m(x)}\dots e^{x_B-m(x)}\right],\ell (x):=\sum _{i}f(x{)}_i,\mathrm{softmax}(x):=\frac{f(x)}{\ell (x)}.$$

对于向量 ${\mathbf{x}}^{(1)},{\mathbf{x}}^{(2)}\in {\mathbb{R}}^B$，其拼接向量 $x=\left[x^{(1)}{x}^{(2)}\right]\in {\mathbb{R}}^{2B}$ 的 softmax 可分解为:

$$\begin{array}{rlc}& m(x)=m(\left[x^{(1)}{x}^{(2)}\right])=\max (m(x^{(1)}),m(x^{(2)})),f(x)=\left[e^{m(x^{(1)})-m(x)}f(x^{(1)})e^{m(x^{(2)})-m(x)}f(x^{(2)})\right],& \ell (x)=\ell (\left[x^{(1)}{x}^{(2)}\right])=e^{m(x^{(1)})-m(x)}\ell (x^{(1)})+e^{m(x^{(2)})-m(x)}\ell (x^{(2)}),\mathrm{softmax}(x)=\frac{f(x)}{\ell (x)}.\end{array}$$

因此，如果跟踪记录一些额外的统计量 $(m(x),\ell (x))$，就可以一次计算一个块的 softmax。这样，将输入 $\mathbf{Q},\mathbf{K},\mathbf{V}$ 拆分为多个块（算法 1 第 3 行），计算 softmax 值以及额外的统计量（算法 1 第 10 行），然后合并结果（算法 1 第 12 行）。

重新计算。作者的目标之一是不为反向传播存储 $O(N^2)$ 量级的中间值。反向传播通常需要矩阵 $\mathbf{S},\mathbf{P}\in {\mathbb{R}}^{N\times N}$ 来计算关于 $\mathbf{Q},\mathbf{K},\mathbf{V}$ 的梯度。然而，通过存储输出 $\mathbf{O}$ 和 softmax 归一化统计量 $(m,\ell )$，作者可以在反向传播时利用 SRAM 中的 $\mathbf{Q},\mathbf{K},\mathbf{V}$ 块很容易地重新计算注意力矩阵 $\mathbf{S}$ 和 $\mathbf{P}$。这可以看作是一种选择性梯度检查点[10,34]的形式。虽然梯度检查点被提出用于减少内存所需的最大值，但所有的实现（据我们所知）都必须以速度换取内存。相比之下，即使会有更多的 FLOPs，但由于减少了对 HBM 的访问，作者的重新计算加快了反向传播速度（见图 2）。完整的反向传播描述见附录 B。

实现细节：核融合。分块使作者能够在单个CUDA内核中实现作者的算法，从 HBM 中加载输入，执行所有的计算步骤（矩阵乘法，softmax，可选的掩码和dropout，矩阵乘法），然后将结果写回 HBM（掩码和 dropout 见附录B）。这避免了对 HBM 输入和输出的反复读写。

作者证明了 FlashAttention 的正确性、运行时间和内存需求（证明见附录 C）。

定理1. 算法 1 返回 $\mathbf{O}=\mathrm{softmax}(\mathbf{Q}{\mathbf{K}}^{\top })\mathbf{V}$，其浮点运算量为 $O(N^{2}d)$，且除了输入和输出外，还需要 $O(N)$ 的额外内存空间。

3.2 Analysis: IO Complexity of FlashAttention

作者分析了 FlashAttention 的 IO 复杂度，证明其相较于标准注意力显著减少了 HBM 访问次数。作者也提供了一个下界，证明在所有 SRAM 大小的情况下，没有任何精确注意力算法能够渐近优化 HBM 访问次数。相关证明见附录 C。

定理2. 设 $N$ 为序列长度，$d$ 为头维度，$M$ 为 SRAM 的大小，满足 $d\le M\le Nd$。标准注意力（算法 0）需要 $\Theta (Nd+N^2)$ 次 HBM 访问，而 FlashAttention（算法 1）需要 $\Theta (N^2{d}^2{M}^{-1})$ 次 HBM 访问。

对于典型的 $d$ 值（64–128）和 $M$ 值（约 100KB），由于 $d^2$ 远小于 $M$，FlashAttention 相较于标准实现所需的 HBM 访问次数大大减少。这带来了更快的执行速度和更低的内存占用，作者在第 4.3 节中对此进行了验证。

该证明的核心思想是：给定 SRAM 大小为 $M$，作者可以加载大小为 $\Theta (M)$ 的 $\mathbf{K}$、$\mathbf{V}$ 块（算法 1 第 6 行）。对于每个 $\mathbf{K}$、$\mathbf{V}$ 块，作者遍历所有 $\mathbf{Q}$ 的块（算法 1 第 8 行）以计算中间值，从而产生 $\Theta (Nd{M}^{-1})$ 次对 $\mathbf{Q}$ 的访问。每次访问加载 $\Theta (Nd)$ 个元素，总计为 $\Theta (N^2{d}^2{M}^{-1})$ 次 HBM 访问。类似地，作者证明了标准注意力的反向传播需要 $\Theta (Nd+N^2)$ 次 HBM 访问，而 FlashAttention 的反向传播仅需 $\Theta (N^2{d}^2{M}^{-1})$ 次（详见附录 B）。

作者证明了一个下界：在计算精确注意力时，对于所有可能的 $M$ 值（即 SRAM 大小），在 HBM 的访问次数上都无法实现渐近优化。

命题3. 设 $N$ 为序列长度，$d$ 为头维度，$M$ 为 SRAM 的大小，满足 $d\le M\le Nd$。对于区间 $[d,Nd]$ 内所有 $M$ 值，不存在一个算法以 $o(N^2{d}^2{M}^{-1})$ 次的 HBM 访问次数来计算精确注意力。

该证明基于以下事实：当 $M=\Theta (Nd)$ 时，任何算法都必须执行 $\Omega (N^2{d}^2{M}^{-1})=\Omega (Nd)$ 次 HBM 访问。这种在 $M$ 的子区间上的下界在流式算法文献[88]中是很常见的。作者将在 $M$ 方面的参数化复杂度下界证明留作未来值得探索的方向。

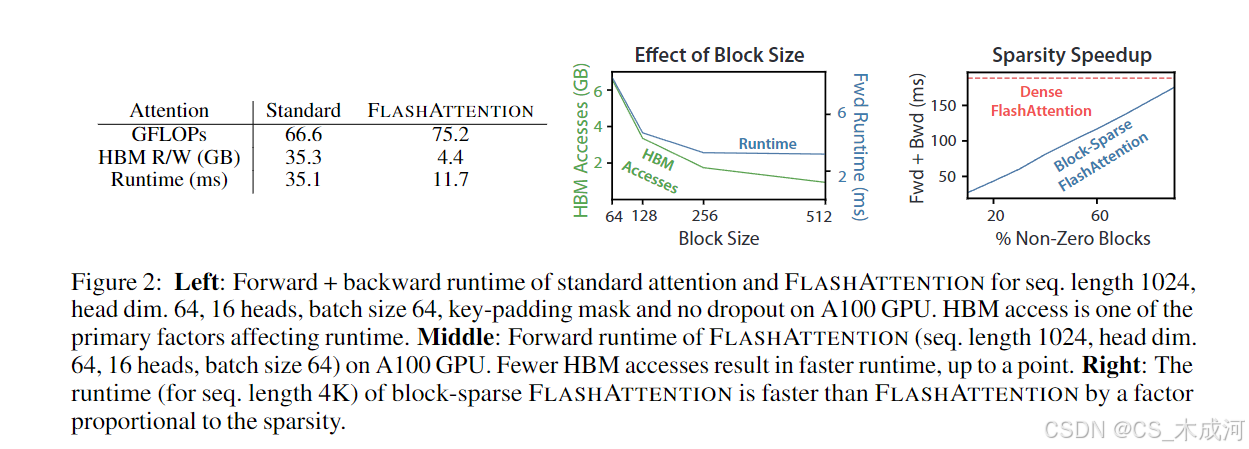
作者验证了 HBM 访问次数是注意力运行时间的主要决定因素。在图 2（左）中可以看到，尽管 FlashAttention 相较于标准注意力具有更高的 FLOP 数量（由于反向传播中的重新计算），但它具有更少的 HBM 访问，从而带来了更快的运行时间。在图 2（中）中，作者通过调整 FlashAttention 的块大小 $B_c$，进而产生不同的 HBM 访问次数，并测量前向传播的运行时间。随着块大小的增加， HBM 访问次数减少（因输入数据遍历次数变少），运行时间也随之减少。对于足够大的块大小（超过 256），运行时间受到其他因素（如算术运算）的制约。此外，较大的块大小将无法融入较小的 SRAM 中。

3.3 Extension: Block-Sparse FlashAttention

作者将 FlashAttention 扩展到近似注意力：作者提出了块稀疏 FlashAttention，其 IO 复杂度比 FlashAttention 小了一个与稀疏度成比例的因子。给定输入 $\mathbf{Q},\mathbf{K},\mathbf{V}\in {\mathbb{R}}^{N\times d}$ 和掩码矩阵 M ~ ∈ { 0 , 1 } N × N \tilde{\mathbf{M}} \in \{0,1\}^{N \times N} M~∈{0,1}N×N，作者需要计算：

$$\mathbf{S}=\mathbf{Q}{\mathbf{K}}^{\top }\in {\mathbb{R}}^{N\times N},\mathbf{P}=\mathrm{softmax}(\mathbf{S}\odot 1_{\tilde{\mathbf{M}}})\in {\mathbb{R}}^{N\times N},\mathbf{O}=\mathbf{PV}\in {\mathbb{R}}^{N\times d},$$

其中，当 ${\tilde{\mathbf{M}}}_{kl}=1时$，$(\mathbf{S}\odot 1_{\tilde{\mathbf{M}}}{)}_{kl}={\mathbf{S}}_{kl}$；当 ${\tilde{\mathbf{M}}}_{kl}=0$，$(\mathbf{S}\odot 1_{\tilde{\mathbf{M}}}{)}_{kl}=-\infty$。作者要求 $\tilde{\mathbf{M}}$ 具有块状结构：存在块大小 $B_r,B_c$，对所有 $k,l$，存在 M ∈ { 0 , 1 } N / B r × N / B c \mathbf{M} \in \{0,1\}^{N/B_r \times N/B_c} M∈{0,1}N/Br​×N/Bc​，使得有 ${\tilde{\mathbf{M}}}_{k,l}={\mathbf{M}}_{ij}$，其中 $i=\lfloor k/B_r\rfloor$，$j=\lfloor l/B_c\rfloor$。

给定预定义的块稀疏掩码 M ∈ { 0 , 1 } N / B r × N / B c \mathbf{M} \in \{0,1\}^{N/B_r \times N/B_c} M∈{0,1}N/Br​×N/Bc​，作者可以轻松地调整算法 1 以仅计算注意力矩阵的非零块。除了跳过零块计算，该算法与算法 1 完全相同。作者在附录 B 的算法 5 中重述了该算法描述。

作者还分析了块稀疏 FlashAttention 的 IO 复杂度。

命题4. 设 $N$ 为序列长度，$d$ 为头维度，$M$ 为 SRAM 的大小，满足 $d\le M\le Nd$。块稀疏 FlashAttention（算法 5）需要 $\Theta (Nd+N^2{d}^2{M}^{-1}s)$ 次 HBM 访问，其中$s$ 是块稀疏掩码中非零块所占的比例。

作者观察到，应用块稀疏性可以通过稀疏度对 IO 复杂度中的主要项进行直接优化。对于较大的序列长度 $N$，稀疏度 $s$ 通常设置为 $N^{-1/2}$ [11] 或 $N^{-1}\log N$ [3, 17, 92]，对应 $\Theta (N\sqrt{N})$ 或 $\Theta (N\log N)$ 的 IO 复杂度。在下游实验中，作者使用了固定的蝴蝶稀疏模式[17]，该模式已被证明可以近似任意稀疏结构[16]。

在图 2（右）中，作者验证了随着稀疏度的增加，块稀疏 FlashAttention 的运行时间呈比例改善。在 LRA 基准测试中，块稀疏 FlashAttention 实现了 2.8 倍的加速，同时在性能上与标准注意力相当（见第 4 节）。

4 Experiments

作者评估了使用 FlashAttention 训练 Transformer 模型的影响。作者验证了关于训练时间和模型准确率的两个论点，并报告了注意力运行时间和内存基准表现。

• 训练速度。FlashAttention 以 15% 的优势超越了 MLPerf 1.1[58] 中 BERT 的训练速度纪录，相较于标准 Transformer，FlashAttention 在训练 GPT-2 时比 HuggingFace [87] 提速 3 倍，比Megatron [77] 提速 1.8 倍。在 Long-Range Arena (LRA) 基准测试中，FlashAttention 实现了 2.4 倍的加速。

• 模型质量。FlashAttention 将 Transformer 拓展到更长的序列，从而提升模型质量。FlashAttention 在训练上下文长度为 4K 的 GPT-2 时速度快于 Megatron 训练上下文长度为 1K 的 GPT-2，同时困惑度降低了 0.7。对更长序列进行建模，使得两项长文档分类任务的性能提升了6.4个百分点。最后，FlashAttention 产生了首个在具有挑战性的 Path-X 任务（序列长度 16K） 上实现优于随机水平的 Transformer 模型，同时块稀疏 FlashAttention 产生了我们所知的首个在 Path-256（序列长度 64K） 上实现优于随机水平的序列模型。

• 基准注意力。作者测量了 FlashAttention 和块稀疏 FlashAttention 在不同序列长度下的运行时间和内存性能情况。作者验证了 FlashAttention 的内存占用随序列长度线性增长，并且在常见序列长度（≤ 2K）下比标准注意力快达 3 倍。作者也验证了块稀疏 FlashAttention 的运行时间随序列长度线性增长，并且在速度上超过了所有现有的近似注意力基线方法。

其他实验细节见附录 E。

4.1 Faster Models with FlashAttention

BERT. FlashAttention 产生了作者已知的最快的单节点 BERT 训练速度。作者使用 FlashAttention 在 Wikipedia 上训练了一个 BERT-large 模型。表 1 对比了作者的训练时间与 Nvidia 的实现（其在 MLPerf 1.1 [58] 中创下的训练速度记录）。作者的实现快了 15%。

GPT-2. FlashAttention 在大规模 OpenWebText 数据集 [32] 上 GPT-2 [67] 的训练速度比广泛使用的 HuggingFace [87] 和 Megatron-LM [77] 实现更快。表 2 显示，与 HuggingFace 相比最高可实现 3 倍的端到端加速，与 Megatron-LM 相比有 1.7 倍的加速。由于作者没有改变模型定义，FlashAttention 和其他两种实现达到了相同的困惑度。附录 E 包含了训练过程中验证困惑度的曲线图，证明了 FlashAttention 与基线方法具有相同的数值稳定性，并产生了相同的训练/验证曲线。

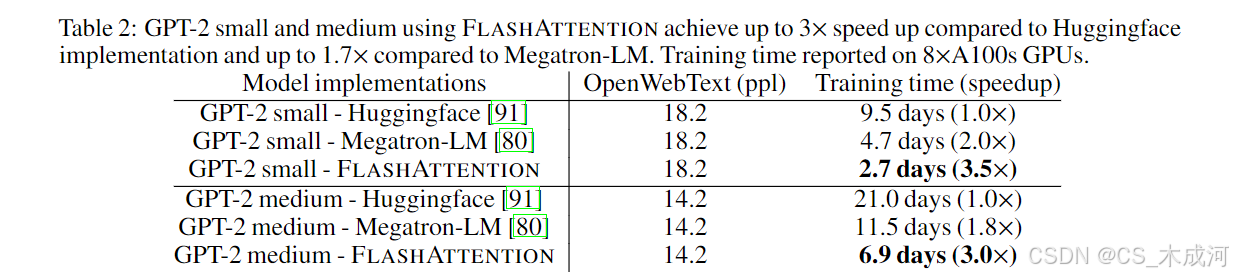
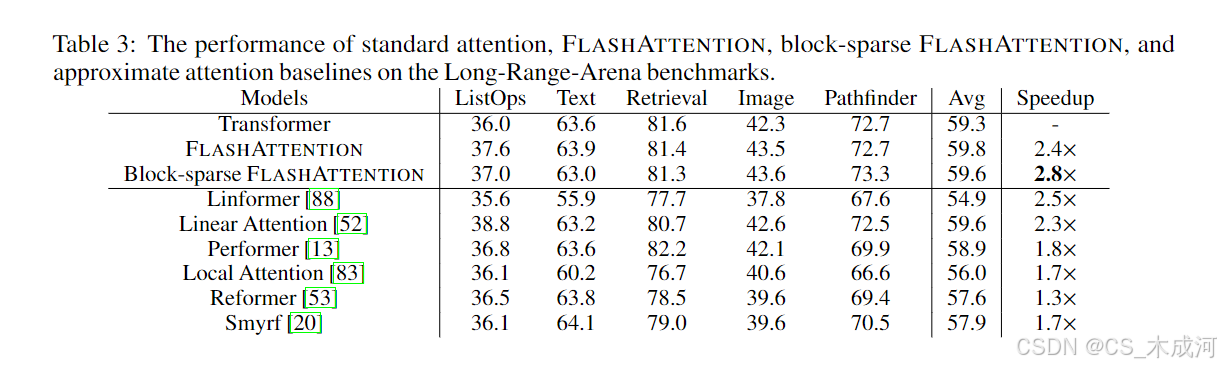
Long-range Arena（LRA）. 作者在 LRA [80]基准上对比了 vanilla Transformer（使用标准实现或 FlashAttention）。作者测量了所有模型的准确率、吞吐量和训练时间。每个任务具有不同的序列长度，在 1024 到 4096 之间变化。作者遵循 Tay 等人[80]和 Xiong 等人[90]的实现与实验设置。表 3 显示，FlashAttention 相比标准注意力实现了高达 2.4 倍的加速。块稀疏 FlashAttention 快于作者测试过的所有近似注意力方法。

4.2 Better Models with Longer Sequences

长上下文语言建模。FlashAttention 的运行时间和内存效率使作者能够将 GPT-2 的上下文长度增加到原来的 4 倍，同时其仍然比 Megatron-LM 的优化实现更快。表 4 展示了使用 FlashAttention、上下文长度为 4K 的 GPT-2，仍然比使用 Megatron、上下文长度为 1K 的 GPT-2 快 30%，同时实现了 0.7 更好的困惑度。

长文档分类。采用 FlashAttention 训练更长序列的 Transformer 可以提高在 MIMIC-III [47] 和 ECtHR [6,7] 数据集上的性能。MIMIC-III 包含了重症监护病房患者出院摘要，每份文档标注有多个标签；ECtHR 收录了来自欧洲人权法院的法律案例，每份案例关联涉嫌违反的《欧洲人权公约》具体条款。这两个数据集都包含非常长的文本文档：MIMIC的平均 token 数为 2,395，最长文档达 14,562 个token；ECtHR 的平均和最大 token 数分别为 2,197 和 49,392。作者通过增加预训练 RoBERTa 模型 [56]（重做 Beltagy 等人 [3] 的位置编码）的序列长度来评估性能提升。

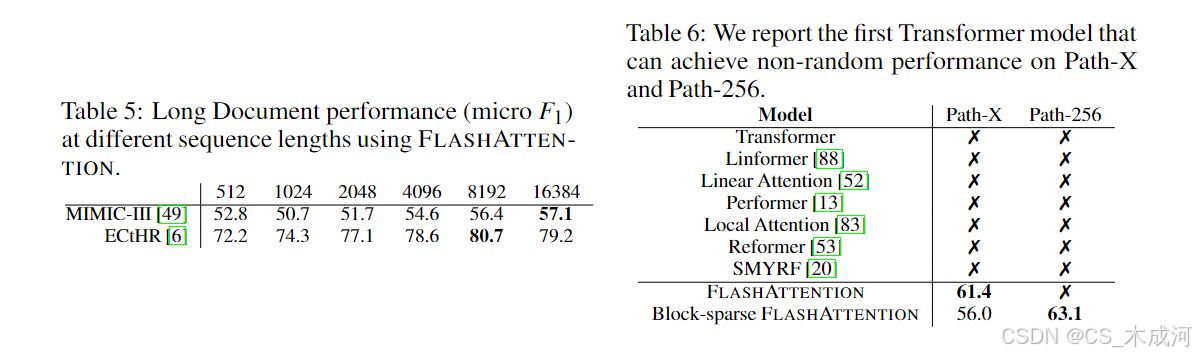
表 5 展示了在 MIMIC 上，序列长度 16K 的性能比长度 512 高出 4.3 个点；在 ECtHR 上，长度 8K 比长度 512 高出 8.5 个点。这种差异可能是由于细微的分布变化：MIMIC-III 包含专业医学文本，因此可能更容易受到文档长度分布变化的影响，而 ECtHR 包含的是通用语言。

Path-X 和 Path-256。Path-X 和 Path-256 基准是 long-range arena (LRA) 基准中的两个具有挑战性的任务，专为测试长上下文建模能力而设计。该任务目标是判断 128×128（或256×256）黑白图像中两个点之间是否存在一条连通路径，图像以逐像素方式输入 Transformer。在以往的研究中，所有 Transformer 模型要么因内存不足而无法运行，要么只能达到接近随机的表现 [80]。因此，研究者一直在寻找可以建模此类长上下文的替代架构 [37]。在这里，作者给出了 Transformer 模型能够解决 Path-X 和 Path-256 的首次结果（见表 6）。作者在 Path-64 上预训练了 Transformer，然后通过空间插值方式扩展位置编码，迁移到 Path-X 上。FlashAttention 在 Path-X 上达到了 61.4% 的准确率。另外，块稀疏 FlashAttention 将 Transformer 扩展到了序列长度为 64K，在 Path-256 上达到了 63.1% 的准确率。

4.3 Benchmarking Attention

作者在配备 40GB HBM 的A100 GPU上，改变序列长度并测量 FlashAttention 和块稀疏 FlashAttention 在不同注意力基准下的运行时间和内存使用情况，同时带有 dropout 和 padding mask。作者与精确注意力、近似注意力以及稀疏注意力的参考实现进行了对比。作者在正文中展示了部分基线结果，更多基准和完整细节可见附录 E。

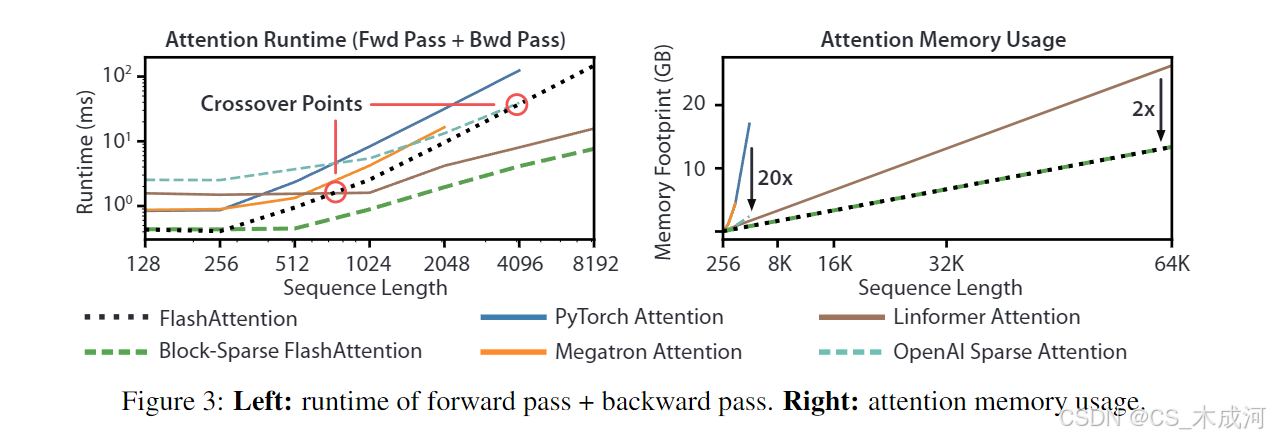
运行时间。图 3（左）展示了 FlashAttention 和块稀疏 FlashAttention 在前向 + 反向传播过程中的运行时间（以毫秒计），并与精确注意力、近似注意力和稀疏注意力的基准实现进行了对比（精确数值见附录 E）。尽管运行时间随着序列长度呈二次增长，FlashAttention 相比精确注意力基准仍运行明显更快，比 PyTorch 实现最高可达 3 倍。许多近似/稀疏注意力机制的运行时间随着序列长度线性增长，但对于短序列，FlashAttention 由于内存访问更少，仍比近似和稀疏注意力运行得更快。在序列长度为 512 到 1024 之间时，近似注意力的运行时间开始与 FlashAttention 持平。另一方面，块稀疏 FlashAttention 在所有序列长度上都比作者已知的所有精确、稀疏和近似注意力实现更快。

内存占用。图 3（右）展示了 FlashAttention 和块稀疏 FlashAttention 相比于多种精确、近似和稀疏注意力基准的内存占用情况。FlashAttention 和块稀疏 FlashAttention 的内存占用相同，且随序列长度线性增长。与精确注意力基准相比，FlashAttention 的内存效率最高可提升达 20 倍，同时比近似注意力基准更节省内存。除 Linformer 以外，其他所有算法在 A100 GPU 上都无法处理长度为 64K 的序列并会耗尽内存，而 FlashAttention 仍然比 Linformer 的内存效率高出 2 倍。

5 Limitations and Future Directions

作者讨论了作者方法的局限性以及未来的研究方向。相关工作见附录 A。

编译为 CUDA。作者当前构建 IO 感知注意力实现的方法需要为每种新的注意力实现编写一个新的 CUDA 内核。这需要使用一种比 PyTorch 更底层的语言来编写注意力算法，并且需要大量的工程工作。此外，这些实现可能无法在不同的 GPU 架构之间迁移。这些局限性表明需要一种支持使用高级语言（例如 Pytorch）编写注意力算法的方法，并将其编译为 IO 感知的 CUDA 实现——类似于图像处理领域中的 Halide 项目 [70]。

IO 感知的深度学习。作者认为这种 IO 感知的方法可以扩展至注意力之外。虽然注意力是 Transformer 中内存开销最大的计算，但深度网络中的每一层都会访问 GPU 的 HBM。作者希望作者的工作能够激发其他模块的 IO 感知实现。作者在附录 D 中讨论了这些潜在的扩展方向。

多 GPU 的 IO 感知方法。作者提出的注意力机制的 IO 感知实现在单个 GPU 上的计算达到了常数范围内的最优。然而，注意力计算可以在多个 GPU 之间并行化 [72]。使用多个 GPU 会为 IO 分析增加一个额外的层——考虑 GPU 之间的数据传输。作者希望本研究能够激发在该方向上的更多后续工作。

论文链接：NeurIPS-2022-flashattention-fast-and-memory-efficient-exact-attention-with-io-awareness-Paper-Conference

代码地址：https://github.com/Dao-AILab/flash-attention