【leetcode】位运算 - 比特位计数

题目：
给你一个整数 n ，对于 0 <= i <= n 中的每个 i ，计算其二进制表示中 1 的个数 ，返回一个长度为 n + 1 的数组 ans 作为答案。

示例 1：

输入：n = 2
输出：[0,1,1]
解释：
0 --> 0
1 --> 1
2 --> 10

示例 2：

输入：n = 5
输出：[0,1,1,2,1,2]
解释：
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101

提示：

0 <= n <= 105

进阶：

很容易就能实现时间复杂度为 O(n log n) 的解决方案，你可以在线性时间复杂度 O(n) 内用一趟扫描解决此问题吗？
你能不使用任何内置函数解决此问题吗？（如，C++ 中的 __builtin_popcount ）

如果没有加入限制可以使用java的内置函数

Integer.bitCount

---

思路一：
使用右移以及数多少个1的思路

class Solution {
    public int[] countBits(int n) {
        int[] bits = new int[n + 1];
        for (int i = 0; i <= n; i++) {
            bits[i] = countOnes(i);
        }
        return bits;
    }

    public int countOnes(int x) {
        int ones = 0;
        while (x > 0) {
            ones+=x & 1;
            x>>=1;
        }
        return ones;
    }
}

或者将其并在一起

class Solution {
    public int[] countBits(int n) {
        int[] bits = new int[n + 1];
        for (int i = 0; i <= n; i++) {
            bits[i] = bits[i >> 1] + (i & 1);
        }
        return bits;
    }
}

---

思路二：
进行位运算
有多少个1就执行多少次

class Solution {
    public int[] countBits(int n) {
        int[] bits = new int[n + 1];
        for (int i = 0; i <= n; i++) {
            bits[i] = countOnes(i);
        }
        return bits;
    }

    public int countOnes(int x) {
        int ones = 0;
        while (x > 0) {
            x &= (x - 1);
            ones++;
        }
        return ones;
    }
}

但如果将其函数一起写入for之内
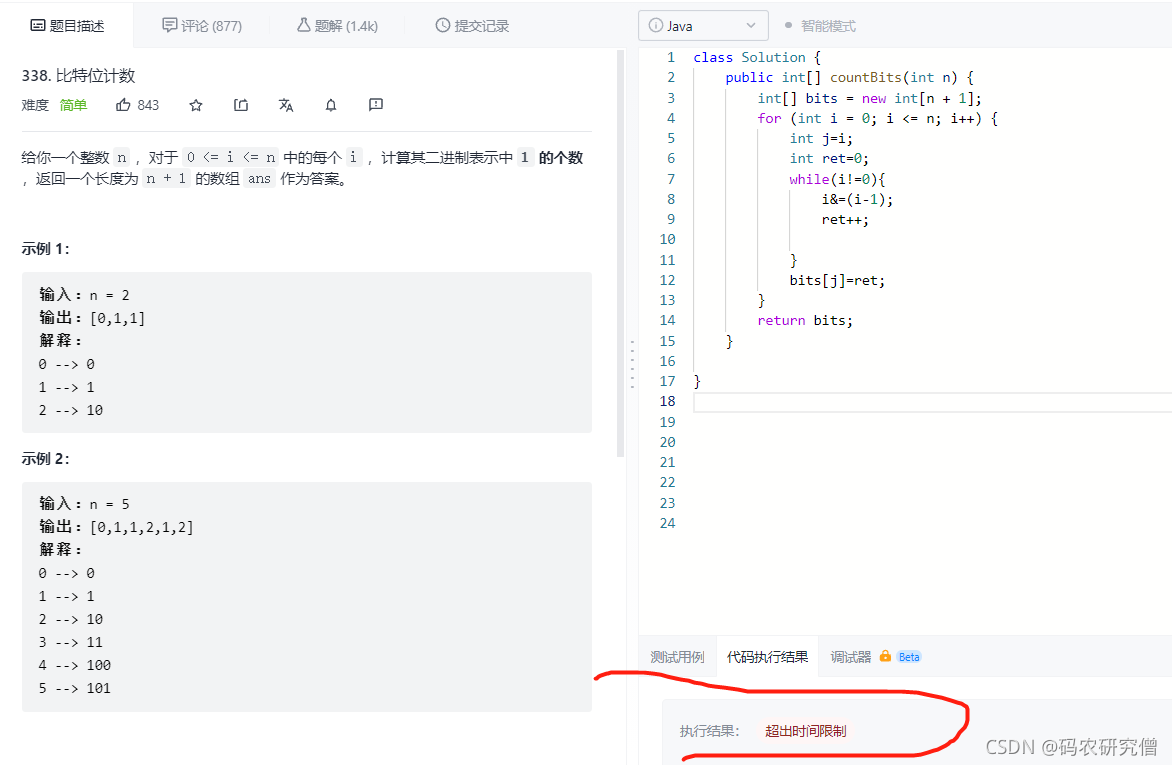
会显示超时限

具体原因好像是
局部变量在栈里面，全局在堆里面。一直循环，堆里面数据不gc只会更多那就会更卡，栈的话在循环的时候，编译器会自动释放，但是堆会越来越多

class Solution {
    public int[] countBits(int n) {
        int[] bits = new int[n + 1];
        for (int i = 0; i <= n; i++) {
            int j=i;
            int ret=0;
            while(i!=0){
                i&=(i-1);
                ret++;
                
            }
            bits[j]=ret;
        }
        return bits;
    }

}

---

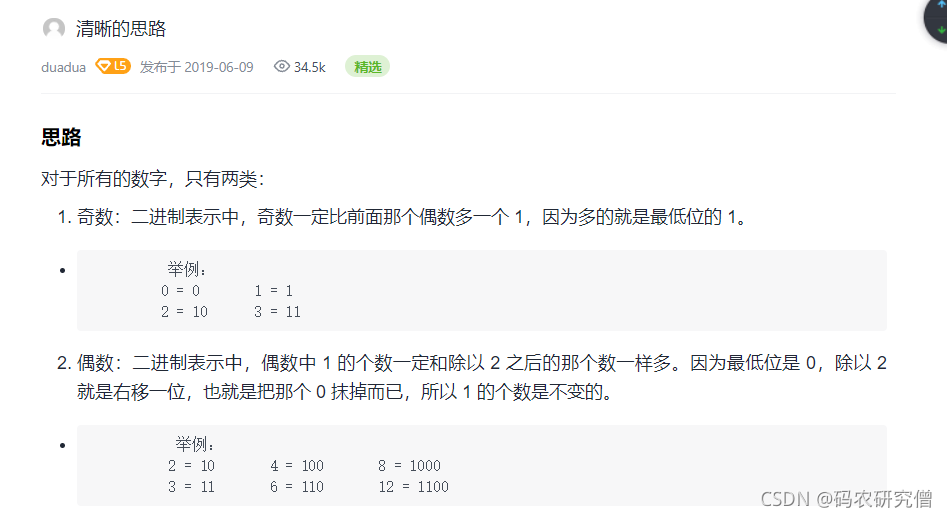
思路三：

运用奇偶数的判断

class Solution {
    public int[] countBits(int n) {
        int[] result = new int[n + 1];
         result[0]=0;
         for(int i = 1; i <= n; i++)
        {
            if(i % 2 == 1)
            {
                result[i] = result[i-1] + 1;
            }
            else
            {
                result[i] = result[i/2];
            }
        }
        
        return result;

    }
}