算法解析：数组与排序问题的高效解决方案-优快云博客

 public int maxArea(int[] height) {
        //左边界和右边界
        int left = 0;
        int right = height.length-1;
        //保存结果的临时变量
        int res = 0;
        while(left<right) {
            //计算高
            int h = Math.min(height[left], height[right]);
            //求容器容量的最大值
            res = Math.max(res, h*(right-left));
            //移动最小值高的一边
            if(height[left]<height[right]) {
                left++;
            }else {
                right--;
            }
        }
        return res;
    }

二.求两个正序数组的中位数

1.题目

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

示例：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

2.图解

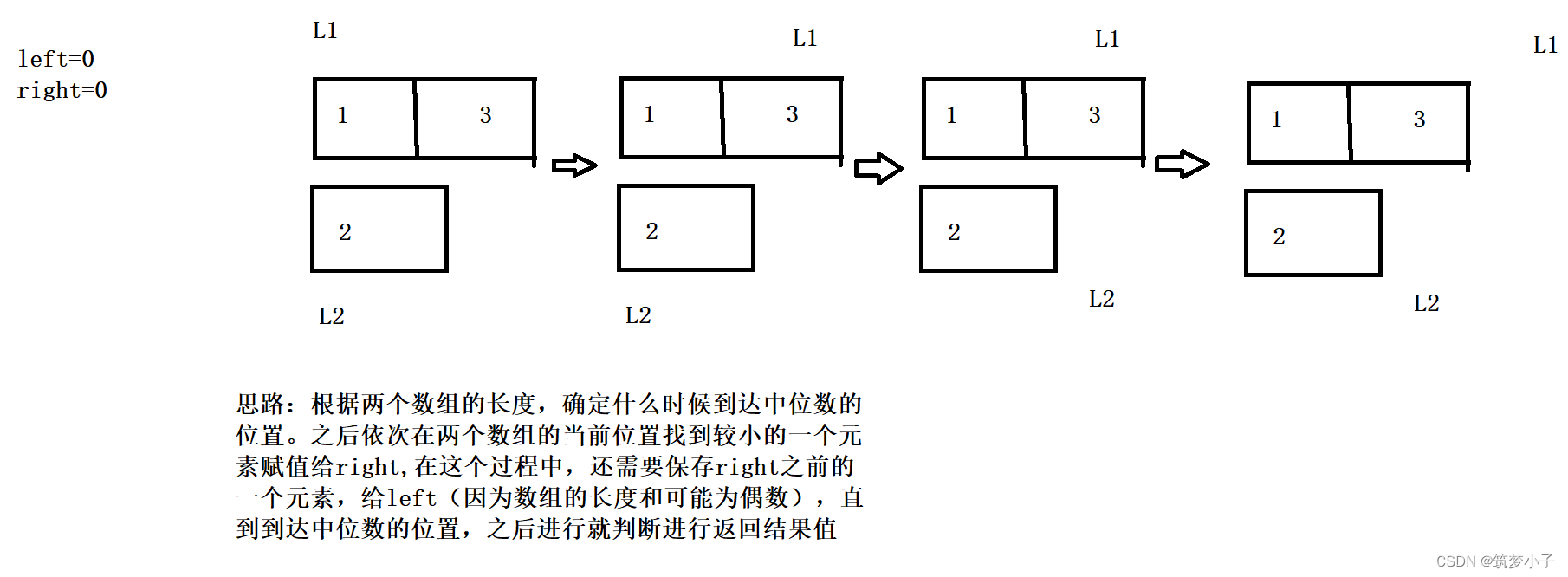
3.代码

 public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int m = nums1.length;
        int n = nums2.length;
        //两个数组开始的位置
        int l1 = 0;
        int l2 = 0;
        //存储中位数的当前值和前一个值
        int left = 0;   
        int right = 0;
        //循环截至到中位数的位置
       for(int i=0; i<=(m+n)/2; i++) {
           left = right;
           //当l1没有超过nums1数组下标时
            //nums1的值小于nums2的值，或者nums1的的元素数比nums2的元素数多，直接从nums1向后找
           if(l1<m && (l2>=n || nums1[l1]<nums2[l2])) {
               right  = nums1[l1++];
           }else {
               right = nums2[l2++];
           }
       }
       //保存最终结果
       double num = 0;
       if((m+n)%2==0) {
           //偶数个
            num = (left+right)/2.0;
       }else {
           num = right;
       }
        return num;
    }

三.组合总和

1.题目

给你一个无重复元素的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有不同组合，并以列表形式返回。你可以按任意顺序返回这些组合。

candidates 中的同一个数字可以无限制重复被选取。如果至少一个数字的被选数量不同，则两种组合是不同的。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/combination-sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

示例：

输入: candidates = [2,3,5] 
target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

数组的数字可以重复，只要满足目标元素的数组即可

2.图解

3.代码

public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<>();
        if(candidates==null || candidates.length==0) {
            return res;
        }
        List<Integer> list = new ArrayList<>();
        dfs(res, list, 0, candidates, target);
        return res;
    }
    /**
    res  存储结果的集合
    list 存储目标数组的集合
    index 需要处理元素的位置
    arr 源数组
    target 当为0时就说明已经找到目标数组（每次递归都会距离目标值更近，减法操作）
     */
    public void dfs(List<List<Integer>> res, List<Integer> list, int index, int[] arr, int target){
        //说明已经找到最后也没有找到，就结束
        if(index == arr.length) {
            return;
        }
        //找到了一个数组可以满足目标值
        if(target == 0) {
            res.add(new ArrayList<>(list));
            return;
        }
        //有两种选择，一种是以当前位置继续寻找，一种是递归到下一个元素继续寻找
            //下一个位置寻找
            dfs(res, list, index+1, arr, target);
            //处理当前元素并继续寻找
            if(target-arr[index]>=0) {
                list.add(arr[index]);
                //处理完以当前位置继续寻找
                dfs(res, list, index, arr, target-arr[index]);
                //处理完当前元素后再进行删除即可(尾删)
                list.remove(list.size()-1);
            }
    }

四.在排序数组中查找元素第一个和最后一个位置（时间复杂度O(log N)）

1.题目

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

示例：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

2.图解

3.代码

 public int[] searchRange(int[] nums, int target) {
        int minIdx = nums.length;
        int maxIdx = -1;
        int[] res = new int[2];
        //初始化数组元素为-1
        Arrays.fill(res,-1);
        int left = 0;
        int right = nums.length-1;
        //通过标记来判断是否存在指定的元素
        boolean flag = false;
        //查找左边界
        while(left<=right) {
            int mid = left+(right-left)/2;
            if(nums[mid] >= target) {
                if(nums[mid] == target) flag = true;
                right = mid-1;
            }else {
                left = mid+1;
            }
        }
        //如果没有找到一个元素，那么就直接返回没有找到
        if(!flag) {
            return res;
        }
        //说明左边界存在，保存左边界
        res[0] = left;
        left = 0;
        right = nums.length-1;
        //继续二分查找右边界
        while(left<=right) {
            int mid = left + (right-left)/2;
            if(nums[mid] <= target) {
                left = mid+1;
            }else {
                right = mid-1;
            }
        }
        res[1] = right;
        return res;
    }

五.合并区间

1.题目

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/merge-intervals
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

示例：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

2.图解

3.代码

 public int[][] merge(int[][] intervals) {
        ArrayList<int[]> res = new ArrayList<>();
        //对数组的第一个元素进行排序（这里使用比较器进行排序）
         Arrays.sort(intervals, new Comparator<int[]>() {
            public int compare(int[] interval1, int[] interval2) {
                return interval1[0] - interval2[0];
            }
        });

        //使用lambda表达式来实现比较器
        // Arrays.sort(intervals,((int[] a, int[] b)->{
        //     return a[0]-b[0];
        // }));

        //合并区间到res中
        for(int i=0; i<intervals.length; i++) {
            //获取当前元素的左右范围
            int left = intervals[i][0];
            int right = intervals[i][1];
            //前一个区间的右比当前区间的左大，那么就直接合并，否则就不能合并，需要创建一个新的区间
            if(res.size()==0 || res.get(res.size()-1)[1]<left) {
                //不可以合并
                res.add(new int[]{left, right});
            }else {
                //可以合并
                res.get(res.size()-1)[1] = Math.max(res.get(res.size()-1)[1], right);
            }
        }
    //将list集合转化为数组并进行返回
        return res.toArray(new int[res.size()][2]);
    }

六.旋转图形（二维矩阵旋转90度）

1.示例

2.图解

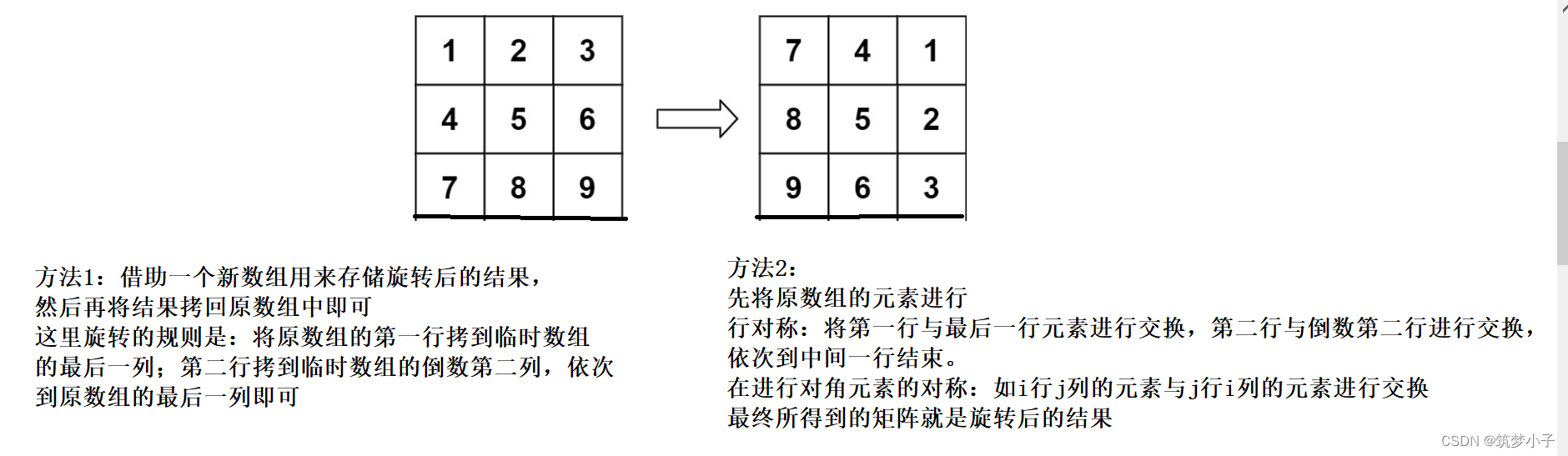
3.代码

/数组旋转90度（时间空间复杂度为O（N^2））
    public void rotate1(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        int[][] tmp = new int[m][n];
        for(int i=0; i<m; i++) {
            for(int j=0; j<n; j++) {
                tmp[j][n-1-i] = matrix[i][j];
            }
        }
        for(int i=0; i<m; i++) {
            for(int j=0; j<n; j++) {
                matrix[i][j] = tmp[i][j];
            }
        }
    }
    //时间复杂度O（N^2），空间复杂度为O(1)
    public void rotate2(int[][] matrix) {
        //行对称
        int m = matrix.length;
        int n = matrix[0].length;
        for(int i=0; i<m/2; i++) {
            for(int j=0; j<n; j++) {
                int tmp = matrix[i][j];
                matrix[i][j] = matrix[m-1-i][j];
                matrix[m-1-i][j] = tmp;
            }
        }
        //对角线对称
        for(int i=0; i<m; i++) {
            for(int j=0; j<i; j++) {
                int tmp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = tmp;
            }
        }
    }

七.消失的数字

1.题目

给你一个含 n 个整数的数组 nums ，其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字，并以数组的形式返回结果。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-all-numbers-disappeared-in-an-array
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

示例：

输入：nums = [4,3,2,7,8,2,3,1]
输出：[5,6]

2.题解思路

（1）借助hash表

首先可以使用一个set集合来记录所有位置的元素，之后再通过遍历从1开始到数组长度的值是否在set中，如果存在就跳过，如果不存在，就将不存在的元素添加到list集合中。

时间复杂度：O(N)

空间复杂度：O(N)

(2)用原始数组充当hash表

首先遍历所有元素，遇到一个元素，首先确定是哪个位置的元素，然后给该位置的元素加上一个这个数组长度的值（nums.length）,之后再遍历这个数组，如果数组中的值小于等于数组长度，说明这个位置的元素没有出现，那么就添加到集合中。

3.代码

//借助额外空间
    public List<Integer> findDisappearedNumbers(int[] nums) {
        List<Integer> res = new ArrayList<>();
        Set<Integer> set = new HashSet<>();
        for(int tmp:nums) {
            set.add(tmp);
        }
        for(int i=1; i<=nums.length; i++) {
            if(!set.contains(i)) {
                res.add(i);
            }
        }
        return res;
    }

//没有使用额外空间
public List<Integer> findDisappearedNumbers2(int[] nums) {
        int n = nums.length;
        List<Integer> list = new ArrayList<>();
        for(int num:nums) {
            int x = (num-1)%n;
            nums[x] += n;
        }
        for(int i=1; i<=n; i++) {
            if(nums[i-1] < n) {
                list.add(i);
            }
        }
        return list;
    }

八.数组的所有子集

1.题目

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。你可以按 任意顺序 返回解集。

示例：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

2.思路图解

使用深度优先搜索来进行处理数组中的元素

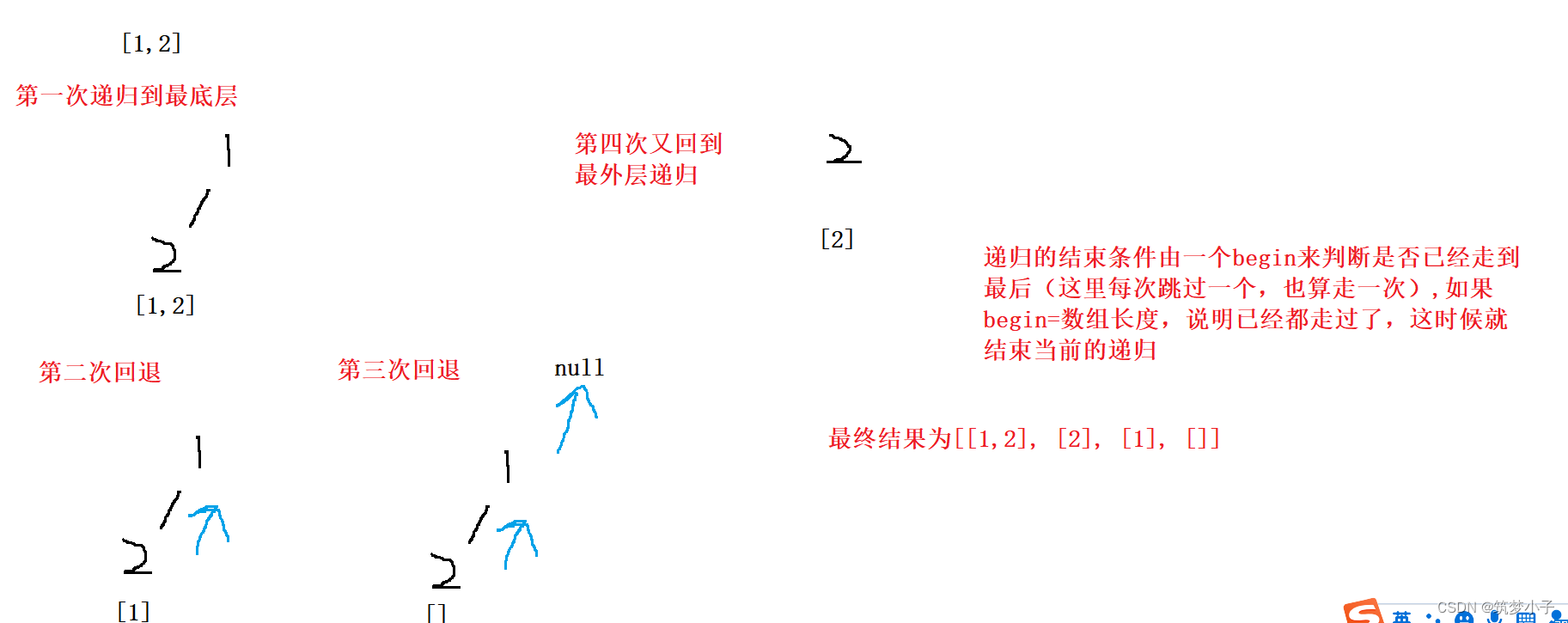
3.代码

  List<List<Integer>> res = new ArrayList<>();
    List<Integer> list = new ArrayList<>();
    public List<List<Integer>> subsets(int[] nums) {
        dfs(nums, 0);
        return res;
    }
    public void dfs(int[] nums, int begin) {
        if(nums.length == begin) {
            res.add(new ArrayList<>(list));
            return;
        }
        //选择当前元素，进行递归
        list.add(nums[begin]);
        dfs(nums, begin+1);
        //不选择当前元素
        list.remove(list.size()-1);
        dfs(nums, begin+1);
    }

九.最长连续序列

1.题目

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为 O(n) 的算法解决此问题。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/longest-consecutive-sequence
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

示例：

输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

2.思路图解

首先将所有元素放到set中（将重复的元素也去除掉了），然后再遍历set集合中的所有元素，如果当前元素没有没有前驱结点在set中，那么就统计当前元素的最大连续序列，最终将统计的结果长度与最大长度作比较，最终返回最大长度即可。

3.代码

public int longestConsecutive(int[] nums) {
        Set<Integer> set = new HashSet<>();
        for(int num:nums) {
            set.add(num);
        }
        int maxLen = 0;
        for(int num:set) {
            //说明该元素没有前驱元素，可以向后寻找连续的序列
            if(!set.contains(num-1)) {
                int tmp = num;
                int len = 1;
                while(set.contains(tmp+1)) {
                    tmp++;
                    len++;
                }
                maxLen = Math.max(maxLen, len);
            }
        }
        return maxLen;
    }