《算法图解》学习笔记（第六章）

《算法图解》学习笔记-第六章-广度优先搜索

---

---

前言

本文为自己的算法学习笔记，用来将所学知识及时输出
所用书籍：《算法图解》

---

6.1 图简介

在数据的逻辑结构D=（KR）中，如果K中结点对于关系R的前趋和后继的个数不加限制，即仅含一种任意的关系，则称这种数据结构为图形结构(百度定义)。
图由节点和边组成，且一个节点可能与众多节点直接相连。
就好似中国的城市就是一个个节点，而连接城市的交通道路就是一条条边。从北京出发可以直接到达天津、唐山、承德、张家口、保定、沧州…而不是只能到达单一目的地。
图分为有向图和无向图：

• 有向图的边为箭头，箭头的方向指明了关系的方向。
  
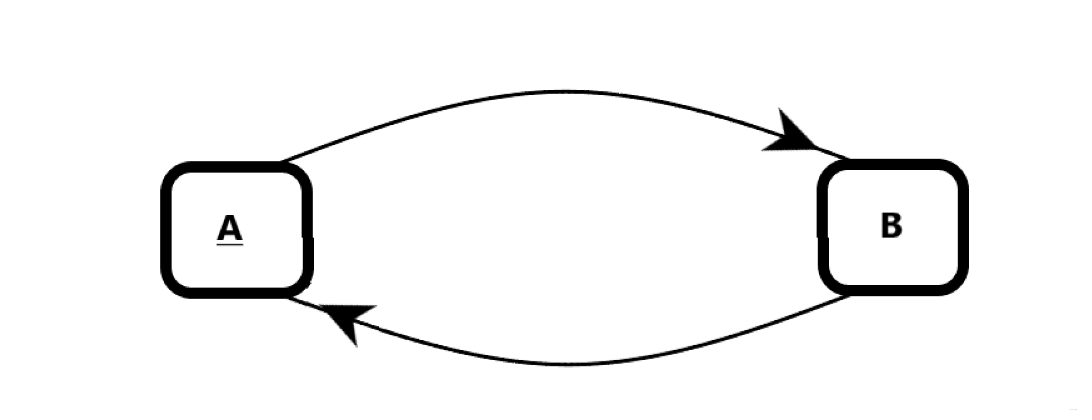
• 无向图的边不带箭头，关系是双向的。
  

---

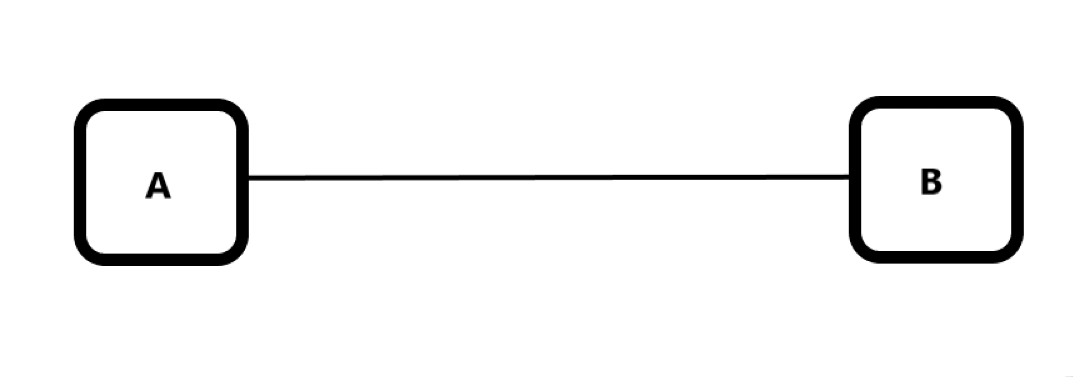
6.2 广度优先搜索

广度优先搜索(BFS breadth-first-search)，是一种用于图形结构的查找算法，其可以解决两类问题：

1. 从A节点出发，有前往B节点的路径吗？
2. 从A节点出发，前往B节点的路径哪条最短？

(1) 是否存在路径

假设你手术大出血，急需适配血源供血，于是医生在你的家人中寻找。

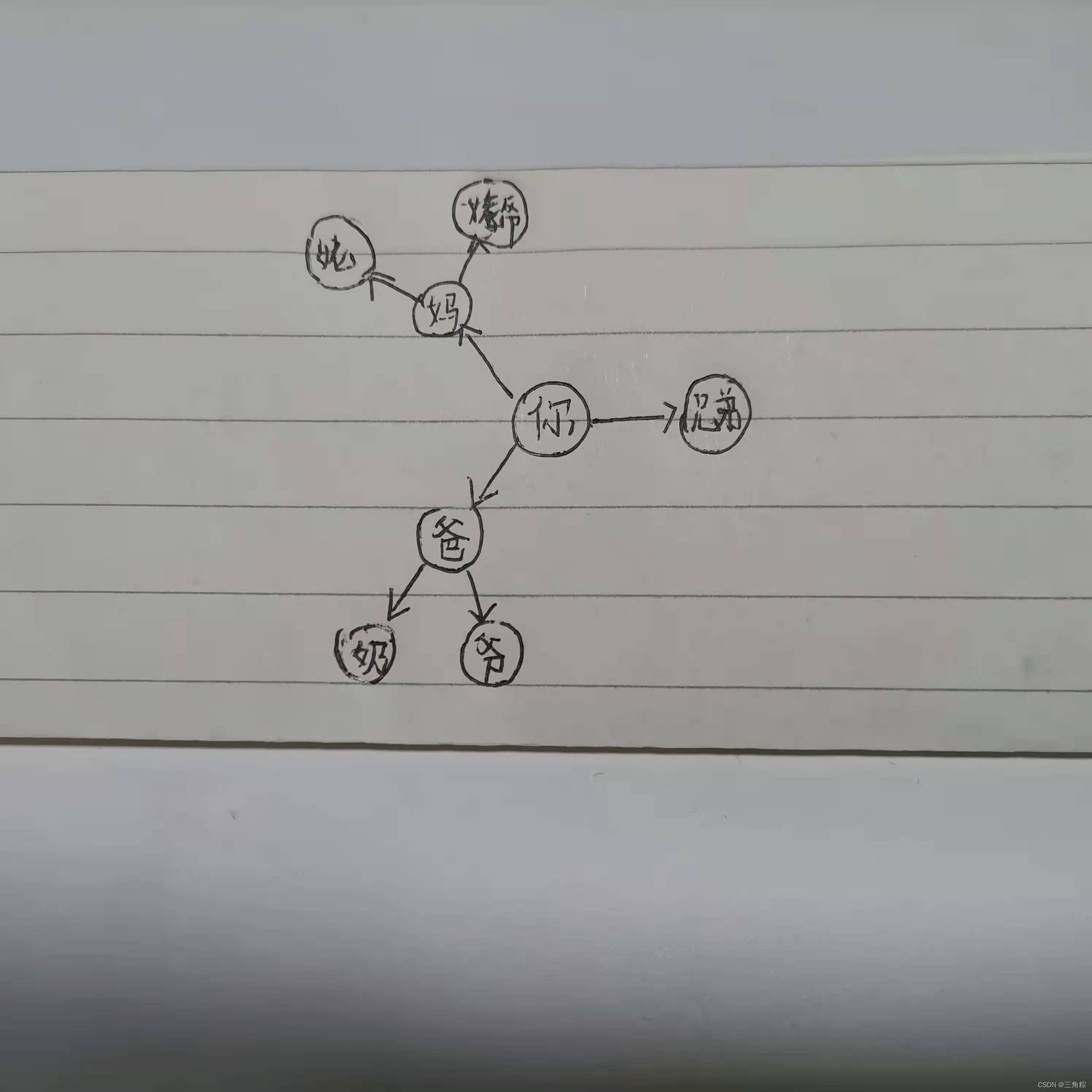
首先查找你的父母和兄弟一辈的，创建一个亲属表单：

父亲

母亲

兄弟

然后依次检查名单中的每个人，看看有没有和你血型匹配的。假设你的家人没有与你血型匹配的，那就去查找你的爷爷辈的亲属：

爷爷

奶奶

母亲

兄弟

检查名单中的每个人，都将其下一级亲属添加进来，这样一来查找的广度越来越宽。这就是广度优先搜索法。

(2) 查找最短路径

上面解决了广度优先搜索可以解决的第一类问题，而第二类问题，如何通过最短路径查找到和血型匹配的亲属。
首先确定哪些亲属和你的关系最近，从图上可以看出，你的父母和兄弟可以看做你的一度关系，而姥姥、姥爷、爷爷、奶奶则是二度关系。我们可以先查找一度关系，确定其中没有和你匹配血型后再查找二度关系。因此找到的是关系最近的适配血型亲属。
注意：需按添加顺序查找才能找到最短路径，如你先查找奶奶，后查找父亲，假设奶奶和父亲都和你的血型匹配，这样你得到的血型匹配的亲属不是关系最近的亲属。因此，需要按添加顺序进行查询，有一个可以实现这样的数据结构————队列。

(3) 队列

队列的工作原理与现实生活中的队列完全一样。队列只支持两种操作：入队和出队。
队列与栈相反，栈是后进先出(LIFO)的数据结构而队列是一种先进先出(FIFO)的数据结构，队尾入队，队头出队。
双向队列：即队头队尾都可进行入队出队操作的队列。

---

6.3 实现图和搜索算法(Python)

代码如下：

from collections import deque

# 创建图
graph = {}
graph['you'] = {'father', 'mother', 'brother'}
graph['father'] = {'grandpa', 'grandma'}
graph['mother'] = {'grandfather', 'grandmother'}
graph['brother'] = {}
graph['grandpa'] = {}
graph['grandma'] = {}
graph['grandfather'] = {}
graph['grandmother'] = {}

# 算法实现
def is_adaptive_blood_group(person):		# 实现血型匹配
	return person == 'grandfather'			# 默认和姥爷血型匹配

def search(name):							# 搜索算法
	search_queue = deque()					# 建立双向队列
	search_queue += graph[name]				# 向队列内添加图结构
	searched = []							# 保存以查找的亲属						
		
	while search_queue:						# 知道队列中亲属均被查找
		person = search_queue.popleft()		# 从左方提取并删除亲属
		if person not in searched:			# 若未被查找
			if is_adaptive_blood_group(person):		# 判断是否属适配血型
				print("{} is your nearest family".format(person))
				return True
			else:
				searched.append(person)				# 对已查询亲属进行标记
				search_queue += graph[person]		# 将二度亲属添加进队列
				
	return False


# test
if __name__ == '__main__':
	search('you')

---

总结

• 有向图由箭头指明关系，无向图关系为双向。
• 广度优先搜索算法可以指出是否有A到B的路径。
• 如果有可以计算出最短路径。
• 面临最短路径问题，可以先用图来建立模型，再用广度优先搜索查找最短路径。
• 队列为先入先出（FIFO）。
• 栈为后入先出（LIFO）。
• 需要按加入顺序进行查询，否则查询到的不是最小路径。
• 检查过的数据不要再进行检查，否则会造成死循环。