气统实习报告四_ynxnt-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_47566615/article/details/122268767

该博客介绍了如何运用一元回归、多元回归和偏相关分析方法，研究全球200hPa位势高度场与热带太平洋ElNino海温和热带印度洋海盆一致模IOB海温异常之间的关系。通过程序实现，计算了各变量间的相关系数，并分析了这些关系的空间分布特征。结果表明，位势高度场与海温异常之间存在复杂的关系，特别是在特定纬度区域显示出显著的正负相关性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

实习四 多元回归分析方法

资料介绍

现有全球200hPa位势高度场资料，文件名NCEP_Z200_30y_Wt.dat，时段：冬季1978~2007年共30年。水平分辨率：7.5*7.5（具体参考NCEP_Z200_30y_Wt.ctl文件），格点数：48*24。

另有热带太平洋海温场资料，文件名NCEP_TPSST_30y_Wt.dat，范围：120~300E，20S~20N. 时段：冬季1978~2007年共30年。水平分辨率：不等距（具体参考NCEP_TPSST_30y_Wt.ctl文件），格点数：32*7。

还有热带印度洋海温场资料，文件名NCEP_IOSST_30y_Wt.dat，范围：35~125E，20S~20N. 时段：冬季1978~2007年共30年。水平分辨率：不等距（具体参考NCEP_IOSST_30y_Wt.ctl文件），格点数：16*7。

要求：（只做 2，3）

1）利用一元回归方法，分析全球200hPa位势高度场分别与热带太平洋El Nino海温和热带印度洋海盆一致模IOB海温异常之间的关系（IOB海温序列可以近似用热带印度洋区域平均海温来表示）。

2）利用多元回归方法，分析全球200hPa位势高度场与热带太平洋El Nino海温和热带印度洋海盆一致模IOB海温异常之间的关系

3）利用偏相关分析方法，分析全球200hPa位势高度场与热带太平洋El Nino海温和热带印度洋海盆一致模IOB海温异常之间的相关关系。

4）比较一元线性回归方法、多元回归方法及偏相关方法分析全球200hPa位势高度场与热带太平洋El Nino海温和热带印度洋海盆一致模IOB海温异常之间的关系，它们之间有什么区别和联系？

一、程序

第二小题

program main

implicit none

integer,parameter::nt=30,nx=48,ny=24,p=2

real IOB(nt),El(nt),Hgt(nx,ny,nt),Hgta(nx,ny) !IOB为热带印度洋海盆一致模，El为热带太平洋El Nino海温，Hgt为全球200hPa位势高度场

real IOBj(nt),Elj(nt),Hgtj(nx,ny,nt) !带j的量为距平值

real x(2,nt),y(nt) !x为预报因子，y为预报量

real::xa(p)=0.0,b(nx,ny,0:p)

real sxx(p,p),sxy(p),sxx_1(p,p) !sxx_1为sxx的逆矩阵

integer it,ix,iy,i,j

open (1,file='D:\2021tj\practice4\IOB_1.grd',form='binary')

read(1)(IOB(it),it=1,nt)

close(1)

!write(*,*)IOB

open(2,file='D:\2021tj\practice4\El.grd',form='binary')

read(2)(El(it),it=1,nt)

close(2)

!write(*,*)El

open(3,file='D:\2021tj\NCEP_Z200_30y_Wt.dat',form='binary')

read(3)(((Hgt(ix,iy,it),ix=1,nx),iy=1,ny),it=1,nt)

close(3)

!write(*,*)Hgt !可知以上三组数组并没有缺测值，以下开始用子程序计算偏相关关系

call jvping(IOB,nt,IOBj) !计算三者的距平值

call jvping(El,nt,Elj)

call jvping_3(Hgt,nx,ny,nt,Hgtj)

do it=1,nt

x(1,it)=Elj(it)

x(2,it)=IOBj(it)

enddo

do ix=1,nx

do iy=1,ny

do i=1,p

do j=1,p

sxx(i,j)=0.0 !x的方差

do it=1,nt

sxx(i,j)=sxx(i,j)+x(i,it)*x(j,it)

enddo

sxx(i,j)=sxx(i,j)/nt

enddo

do i=1,p

sxy(i)=0.0

do it=1,nt

y(it)=Hgt(ix,iy,it) !将每个点的高度场赋值给y

sxy(i)=sxy(i)+x(i,it)*y(it)

enddo

sxy(i)=sxy(i)/nt

enddo

do i=1,p

b(ix,iy,i)=0.0

do j=1,p

call qiuni(sxx,p,sxx_1)

b(ix,iy,i)=b(ix,iy,i)+sxx_1(i,j)*sxy(j) !sxx_1

enddo

Hgta(ix,iy)=0.0

do it=1,nt

Hgta(ix,iy)=Hgta(ix,iy)+Hgt(ix,iy,it)/nt

do i=1,p

xa(i)=xa(i)+x(i,it)/nt

enddo

b(ix,iy,0)=Hgta(ix,iy)

do i=1,p

b(ix,iy,0)=b(ix,iy,0)-b(ix,iy,i)*xa(i)

enddo

open(4,file='D:\2021tj\practice4\b1.grd',form='binary')

write(4)((b(ix,iy,1),ix=1,nx),iy=1,ny)

close(4)

open(5,file='D:\2021tj\practice4\b2.grd',form='binary')

write(5)((b(ix,iy,2),ix=1,nx),iy=1,ny)

close(5)

end program

subroutine jvping(x,nt,y) !一维数组的距平计算

implicit none

integer nt,it

real x(nt),y(nt),ave

ave=0.0

do it=1,nt

ave=ave+x(it)/nt

enddo

do it=1,nt

y(it)=x(it)-ave

enddo

!write(*,*)y

end subroutine

subroutine jvping_3(x,nx,ny,nt,y) !三维数组的距平计算

implicit none

integer nx,ny,nt

real x(nx,ny,nt),y(nx,ny,nt),ave(nx,ny)

integer ix,iy,it

do ix=1,nx

do iy=1,ny

ave(ix,iy)=0.0

do it=1,nt

ave(ix,iy)=ave(ix,iy)+x(ix,iy,it)/nt

enddo

do ix=1,nx

do iy=1,ny

do it=1,nt

y(ix,iy,it)=x(ix,iy,it)-ave(ix,iy)

enddo

end subroutine

subroutine qiuni(x,n,y)

implicit none

integer n,i,j

real x(n,n),y(n,n),x1

y(1,1)=x(2,2)

y(2,2)=x(1,1)

y(1,2)=-x(1,2)

y(2,1)=-x(2,1)

do i=1,n

do j=1,n

x1=x(1,1)*x(2,2)-x(1,2)*x(2,1) !行列式

y(i,j)=y(i,j)/x1

enddo

end subroutine

第三小题

program main

implicit none

integer,parameter::nt=30,nx=48,ny=24

real IOB(nt),El(nt),Hgt(nx,ny,nt) !IOB为热带印度洋海盆一致模，El为热带太平洋El Nino海温，Hgt为全球200hPa位势高度场

real IOBj(nt),Elj(nt),Hgtj(nx,ny,nt) !带j的量为距平值

real r1y(nx,ny),r2y(nx,ny),r12 !r1y为x1与Y的相关系数

real r1y_2(nx,ny),r2y_1(nx,ny) !r1y_2为x1与y在去除了x2影响后的偏相关系数

integer it,ix,iy

open (1,file='D:\2021tj\practice4\IOB_1.grd',form='binary')

read(1)(IOB(it),it=1,nt)

close(1)

!write(*,*)IOB

open(2,file='D:\2021tj\practice4\El.grd',form='binary')

read(2)(El(it),it=1,nt)

close(2)

!write(*,*)El

open(3,file='D:\2021tj\NCEP_Z200_30y_Wt.dat',form='binary')

read(3)(((Hgt(ix,iy,it),ix=1,nx),iy=1,ny),it=1,nt)

close(3)

!write(*,*)Hgt !可知以上三组数组并没有缺测值，以下开始用子程序计算偏相关关系

call jvping(IOB,nt,IOBj) !计算三者的距平值

call jvping(El,nt,Elj)

call jvping_3(Hgt,nx,ny,nt,Hgtj)

!write(*,*)Hgtj

call relative_3(IOBj,Hgtj,nx,ny,nt,r1y) !计算y与x1，y与x2的偏相关关系分别记为r1y,r2y

call relative_3(Elj,Hgtj,nx,ny,nt,r2y)

call relative(IOBj,Elj,nt,r12)

!write(*,*)r12

do ix=1,nx

do iy=1,ny

r1y_2(ix,iy)=(r1y(ix,iy)-r12*r2y(ix,iy))/sqrt((1-r2y(ix,iy)**2)*(1-r12**2))

enddo

do ix=1,nx

do iy=1,ny

r2y_1(ix,iy)=(r2y(ix,iy)-r12*r1y(ix,iy))/sqrt((1-r1y(ix,iy)**2)*(1-r12**2))

enddo

write(*,*)r2y_1

open(4,file='D:\2021tj\practice4\r1y_2.grd',form='binary')

write(4)((r1y_2(ix,iy),ix=1,nx),iy=1,ny)

close(4)

open(5,file='D:\2021tj\practice4\r2y_1.grd',form='binary')

write(5)((r2y_1(ix,iy),ix=1,nx),iy=1,ny)

close(5)

end program main

subroutine jvping(x,nt,y) !一维数组的距平计算

implicit none

integer nt,it

real x(nt),y(nt),ave

ave=0.0

do it=1,nt

ave=ave+x(it)/nt

enddo

do it=1,nt

y(it)=x(it)-ave

enddo

!write(*,*)y

end subroutine

subroutine jvping_3(x,nx,ny,nt,y) !三维数组的距平计算

implicit none

integer nx,ny,nt

real x(nx,ny,nt),y(nx,ny,nt),ave(nx,ny)

integer ix,iy,it

do ix=1,nx

do iy=1,ny

ave(ix,iy)=0.0

do it=1,nt

ave(ix,iy)=ave(ix,iy)+x(ix,iy,it)/nt

enddo

do ix=1,nx

do iy=1,ny

do it=1,nt

y(ix,iy,it)=x(ix,iy,it)-ave(ix,iy)

enddo

end subroutine

subroutine relative_3(xj,yj,nx,ny,nt,r)

implicit none

integer nx,ny,nt,ix,iy,it

real xj(nt),yj(nx,ny,nt),r(nx,ny) !xj，yj为数组的距平

real k(nx,ny),q1(nx,ny),q2(nx,ny) !k为相关系数中的分子 q1为分母第一个，q2为分母第二个

do ix=1,nx

do iy=1,ny

k(ix,iy)=0.0

q1(ix,iy)=0.0

q2(ix,iy)=0.0

r(ix,iy)=0.0

do it=1,nt

k(ix,iy)=k(ix,iy)+xj(it)*yj(ix,iy,it)

q1(ix,iy)=q1(ix,iy)+xj(it)**2

q2(ix,iy)=q2(ix,iy)+yj(ix,iy,it)**2

enddo

r(ix,iy)=k(ix,iy)/sqrt(q1(ix,iy)*q2(ix,iy))

enddo

end subroutine

subroutine relative(xj,yj,nt,r)

implicit none

integer nx,ny,nt,ix,iy,it

real xj(nt),yj(nt),r !xj，yj为数组的距平

real k,q1,q2 !k为相关系数中的分子 q1为分母第一个，q2为分母第二个

k=0.0;q1=0.0;q2=0.0

do it=1,nt

k=k+xj(it)*yj(it)

q1=q1+xj(it)**2

q2=q2+yj(it)**2

enddo

r=k/(sqrt(q1*q2))

end subroutine

二、ctl和gs文件

1.b.ctl

dset D:\2021tj\practice4\b2.grd

undef -999xdef 48 linear 5 7.5

xdef 48 linear 5 7.5

ydef 24 linear -87.5 7.5

zdef 1 levels 1000

tdef 1 linear 00Z01JAN1978 12mo

vars 1

b2 0 99

endvars

2.b.gs

'reinit'

'open D:\2021tj\practice4\b.ctl'

'set lat -90 90'

'set lon 0 360'

'set lev 1000'

'set t 1'

'd b2'

'draw title b2 data'

'gxprint D:\2021tj\practice4\b2.png white'

;

3.r1y_2.ctl

dset D:\2021tj\practice4\r1y_2.grd

undef -999

title r1y_2 data

xdef 48 linear 5 7.5

ydef 24 linear -87.5 7.5

zdef 1 levels 1000

tdef 1 linear 00Z01JAN1978 12mo

vars 1

r1y_2 0 99

endvars

3.r2y_1.gs

'reinit'

'open D:\2021tj\practice4\r1y_2.ctl'

'set lon 0 360'

'set lat -87.5 85'

'set lev 1000'

'set t 1'

'set csmooth on'

'set cterp on'

'd r1y_2'

'set clevs 0'

'set ccolor 1'

'set cthick 8'

'd r1y_2'

'draw title r1y_2'

'gxprint D:\2021tj\practice4\r1y_2.png white'

;

以上文件如r1y_2表示x1和y的去除了x2影响的偏相关系数

三、图形及分析

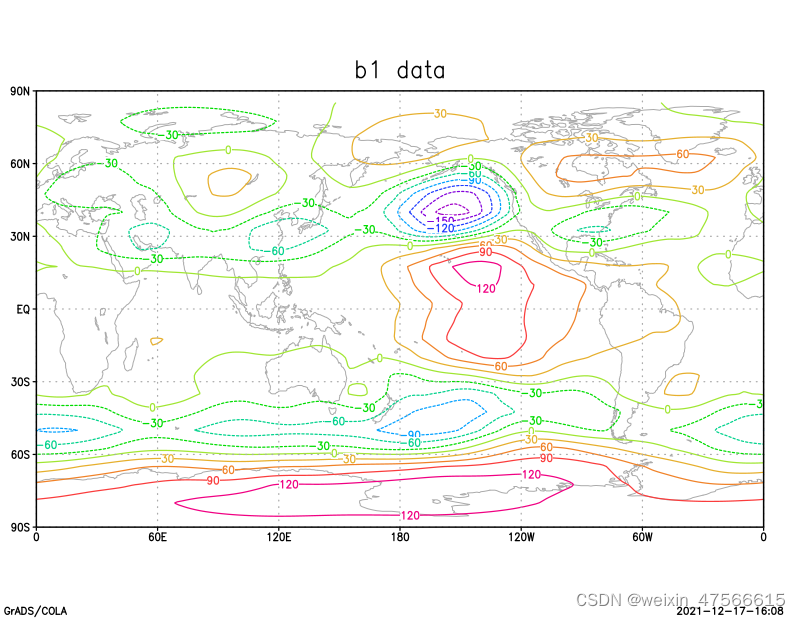
以上是使用协方差矩阵计算出来的b系数的值，可以看出，b1的空间分布图中存在正的大值中心也存在负的大值中心，且负的大值中心处于东太平洋地区；而b2的负大值中心相较于b1更加偏西偏北一些。

X1为热带印度洋海盆一致模IOB海温异常IOBJ，X2为热带太平洋海温距平Elj，Y为位势高度距平值Hgtj

以上两图是x1关于y的去除了x2影响的偏相关系数，以及x2关于y的去除了x1影响的偏相关系数。从图中可以看出，r1y_2大致呈这样的分布，南北中高纬度地区呈负相关，中间低纬度及赤道地区呈正相关，且存在多个正的大值中心，分别位于赤道以及30°N附近，30°S附近，正中心的数值较负中心数值大一些。