《算法导论》学习笔记 第2章：算法入门

1、概况

　　本章插入排序和归并排序两种常见的排序算法来说明算法的过程及算法分析，在介绍归并排序算法过程中引入了分治（divide-and-conquer）算法策略。

2、插入排序

　　(1) 插入排序是简单排序中效率最好的一种，它也是学习其它高级排序的基础，比如希尔排序/快速排序，而他相对于选择排序的优点就在于比较次数几乎少了一半。

　　(2) 插入排序算法思想：

　　　　它的工作机理是通过构建有序序列，对于未排序的数据，在已排好序从后向前扫描，找到相应位置并插入。第一次循环时，将第1个数视为已排好序的数据，从第2个数开始处理。当第2个数 i 与第一个数 i-1 比较时，如果 arr[i] > arr[i-1]，则将 i 和 i - 1 位置进行交换，否则 i，i -1数据不变。此时前两个数形成了一个有序的数据。

　　　　后序循环时，和第一次循环的思路是一样的。当前 i 位置的数据和 i - 1位置的数据比较，如果arr[i] > arr[i-1]，将 i 和 i - 1位置交换，否则数据不变，进入下一次循环。

　　(3) 完整程序如下　　

func insertionSort(arr []int, a, b int) {
　　//判断输入是否合法
    if nil == arr || 0 == len(arr) || a > b || b > len(arr) {
        return
    }
　　//数组下标是从0开始的，从第二个元素开始向前插入
    for i := a + 1; i < b; i++ {
        for j := i; j > a && Less(arr, j, j-1); j-- {
            Swap(arr, j, j-1)
        }
    }
}

//当前数据是否比前一个数据小
func Less(arr []int, i, j int) bool {
    return arr[i] < arr[j]
}

func Swap(arr []int, i int, j int) {
    arr[i], arr[j] = arr[j], arr[i]
}

(4) 算法分析：

　　插入排序过程的时间与输入的规模相关。插入排序的最好情况是输入数组开始时候就是满足要求的排好序的数据，最好时间复杂度为O(n)，在最坏的情况下，输入数组是按逆序排序的，最坏时间复杂度为O(n^2)。其平均时间复杂度是指所有可能的输入实例均以等概率出现的情况下，该算法的运行时间。而一般讨论的时间复杂度往往就是最坏时间复杂度。这是因为最坏情况下的时间复杂度是算法在实例上运行时间的界限，这就保证了算法的运行时间不会比最坏情况更长。所以插入排序的时间复杂度为O(n^2)，通常在输入规模不太大时使用插入排序。其算法是稳定的。

2、归并排序

　　(1) 归并排序采用了算法设计中的分治法，分治法的思想是将原问题分解成n个规模较小而结构与原问题相似的小问题，递归的解决这些子问题，然后再去合并其结果，分治模式在每一层递归上有三个步骤：

　　分解(divide)：将原问题分解成一系列子问题。

　　解决(conquer)：递归地解答各子问题，若子问题足够小，则直接求解。

　　合并(combine)：将子问题的结果合并成原问题的解。

　　归并排序算法按照分治模式，操作如下：

　　分解：将输入规模的n个元素分解成各含n/2个元素的子序列

　　解决：用合并排序法对两个序列递归排序

　　合并：合并两个已排序的子序列以得到排序结果

　　(2) 归并排序算法思想：

　　在对子序列排序时，单个元素被视为已排好序的，所以长度为1时递归结束。归并排序的过程可以在逻辑上抽象成一棵二叉树，树上的每个节点值可以认为是nums[lo...hi]，叶子节点的值就是数组中的单个元素。然后，在每个节点的后续位置(也就是左右子节点已经被排好序)的时候执行merge函数，合并两个子节点上的子数组。这个merge操作会在二叉树的每个节点都执行一边，执行顺序就是二叉树后序遍历顺序。

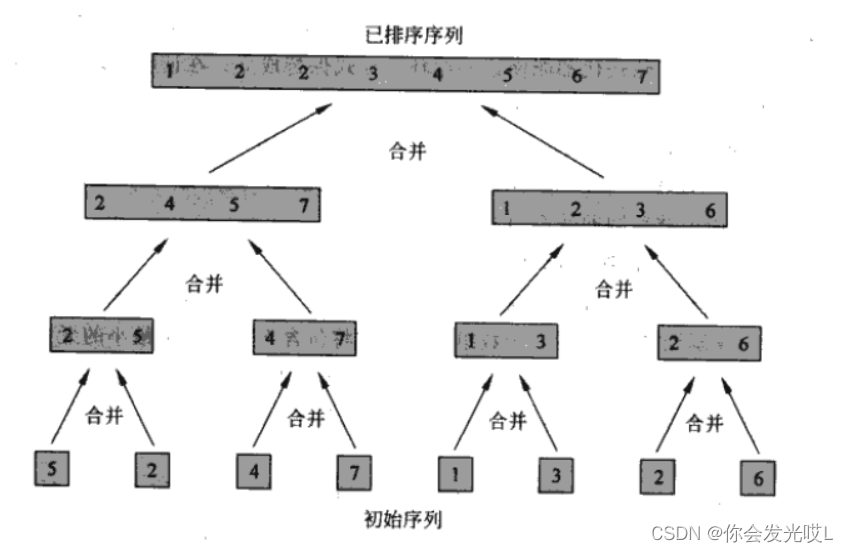
 　(3) 完整程序如下

func Sort(arr []int) {
    temp := make([]int, len(arr))　　//给辅助数组开辟内存空间，这里不在Merge函数执行的时候make辅助数组，避免了在递归中频繁分配和释放内存可能产生的性能问题
    Process(arr, 0, len(arr)-1, temp)　　//排序整个数组，原地修改
}

//将子数组nums[left...right] 进行排序
func Process(arr []int, left int, right int, temp []int) {
    if left == right {　　//单个元素不用排序
        return
    }
    mid := left + (right-left)>>1　　//防止溢出，效果等同于(left+right)>>1，这里使用了右移代替了"/"
    Process(arr, left, mid, temp)　　//先对左半部分数组arr[left...mid]排序
    Process(arr, mid+1, right, temp)　　//再对右半部分数组arr[mid+1...right]排序
    Merge(arr, left, mid, right, temp)　　//将两部分有序数组合并成一个有序数组
}

//将arr[left...mid]和arr[mid+1...right] 这两个有序数组合并成一个有序数组
func Merge(arr []int, left int, mid int, right int, temp []int) {
    for i := left; i <= right; i++ {　　//先把arr[left...right]复制到辅助数组中，以便合并后的结果能直接存入到arr
        temp[i] = arr[i]
    }
    i, j := left, mid+1
    for p := left; p <= right; p++ {　　//数组双指针技巧，合并两个有序数组

        if i == mid+1 {　　//左半边数组已全部合并
            arr[p] = temp[j]
            j++
        } else if j == right+1 {　　//右半边数组已全部合并
            arr[p] = temp[i]
            i++
        } else if temp[i] > temp[j] {
            arr[p] = temp[j]
            j++
        } else {
            arr[p] = temp[i]
            i++
        }
    }
}

　(4) 算法分析：

　　对于归并排序来说，时间复杂度显然集中在merge函数遍历arr[left...right]的过程，在第二点的途中我们可以看到merge执行的次树就是二叉树节点的个数，每次执行的复杂度就是每个节点代表的子数组的长度，所以总的时间复杂度就是整颗树中的个数，也就是数组元素。从图中可以看出，二叉树的高度是logN，每一层的元素个数就是原数组的长度，所以总的时间复杂度就是O(N*logN)。这里的程序的空间复杂度是O(n)，因为我们没有在Merge函数内部为每一小部分子数组开辟内存，避免了在递归时频繁分配内存和释放内存所带来的性能问题。虽然归并排序的时间为O(NlogN)，但是它 很难用于主存排序，因为合并两个排序的表需要线性附加内存，整个算法中还要花费将数据拷贝到临时数组再拷贝回来这样的附加工作，这严重影响排序的速度。

　　归并排序的一个缺点：归并排序需要借助额外的空间。这是因为归并排序的合并函数，在合并两个有序数组为一个有序数组时，需要借助额外的存储空间。我们这里在Merge函数外部开辟了一个O(n)规模的空间，很明显后续的操作都不会再开辟内存，所以空间复杂度为O(n)。但是如果我们在merge函数内部开辟内存呢，空间复杂度是不是就是O(N*logN)了呢？

　　其实不然。实际上递归代码的空间复杂度并不能像时间复杂度那样累加。尽管我们在Merge函数内部，每一次合并操作都额外申请内存空间，但是在合并完成之后，临时开辟的内存空间就被释放了。在任意时刻，CPU只会有一个函数在执行，也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过n个数据的大小，所以空间复杂度也是O(n)。

　　(5) 总结：

　　(1) 对于重要的内部排序应用而言，往往选择快速排序。合并的方法是大多数外部排序算法的基石。

　　(2) 归并排序的空间复杂度时O(n)，并且递归程序的空间复杂度并不能像时间复杂度那样累加，空间复杂度可以看作是一颗二叉树的最大深度。