网络的常见度量属性

1 度分布

网络的度分布p(k)p(k)表示了一个随机选择的节点拥有度kk的概率。我们设度为kk的节点数目Nk=♯ nodes with degree kNk=♯ nodes with degree k，除以节点数量NN则可得到归一化后的概率质量分布：

P(k)=Nk/N(k∈N)P(k)=Nk/N(k∈N)

我们有：∑k∈NP(k)=1∑k∈NP(k)=1。
对于下面这个网络：

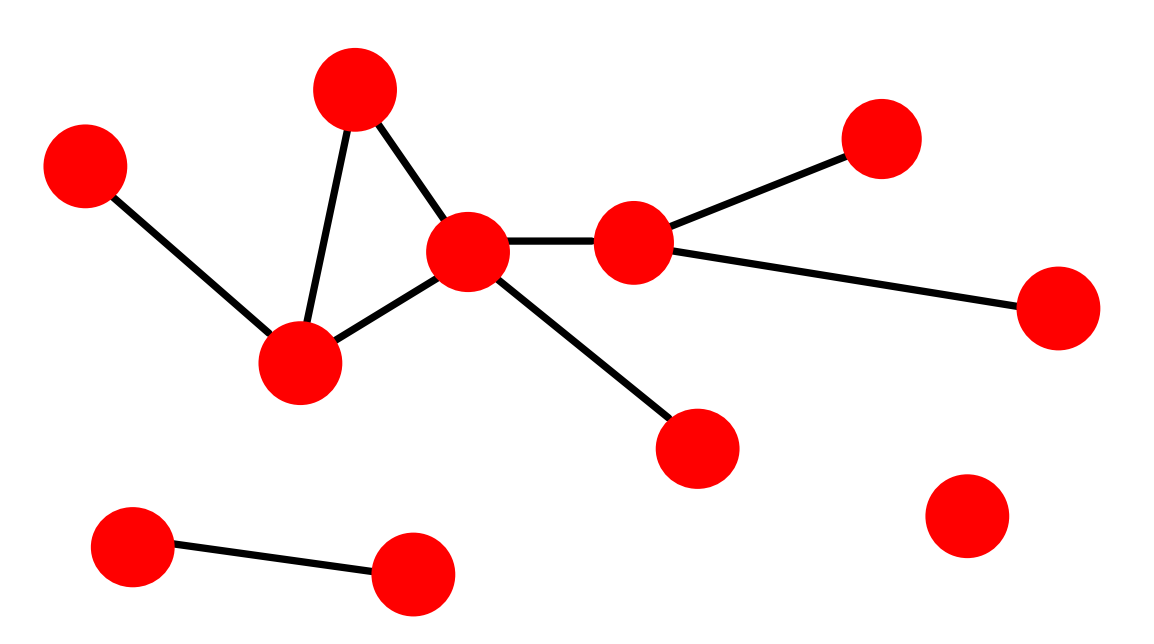
其归一化后的度分布直方图可表示如下：

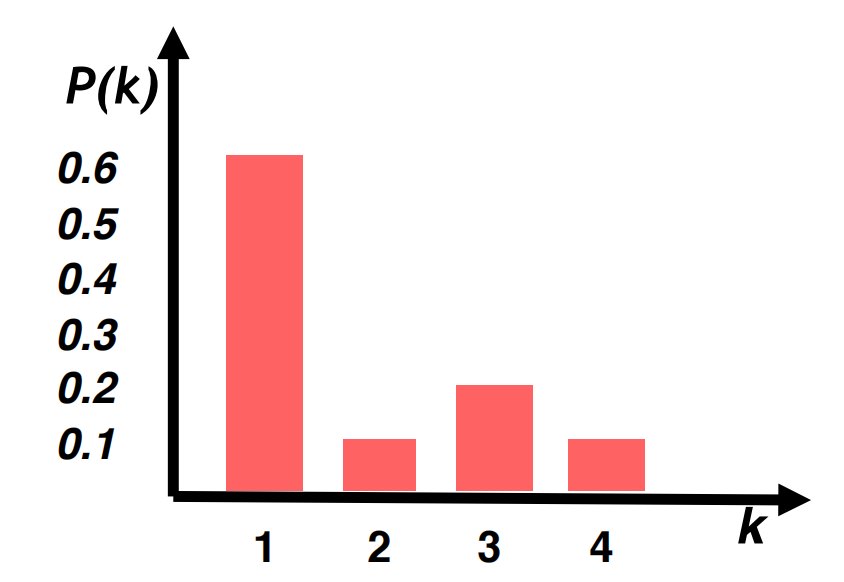
2 路径

2.1 图的路径

图的路径(path)指一个节点序列，使得序列中的每个节点都链接到序列中的下一个节点(注意：这里的术语不同教材不一样，有的教材把这里的路径定义为漫游(walk)，而将术语“路径”保留给简单路径)。路径可以用以下方式进行表示：

Pn={i0,i1,i2,…,in}Pn={(i0,i1),(i1,i2),(i2,i3),…,(in−1,in)}Pn={i0,i1,i2,…,in}Pn={(i0,i1),(i1,i2),(i2,i3),…,(in−1,in)}

一个路径可以通过经过同一条边多次而和它自身相交。如下面这个图中更多路径ABDCDEG就和自身相交。

注意，在有向图中路径只能沿着边的方向。

2