Kmeans聚类的C++实现和Matlab实现

Kmeans聚类的C++实现和Matlab实现

1. 首先介绍Kmeans的工作原理
   Kmeans算法原理比较简单主要步骤为：
   （1）.首先确定我们要把这些已知的点分为几个簇，然后随机选取K个中心点，当然这个中心点的选取在后期是会改变的，不过首先就要确定这个K值，是Kmeans聚类算法的一个缺点吧。
   （2）.计算空间中所有点距离K个中心点的欧氏距离，数据点距离哪个中心点最近，就将此点划分到该点的簇中。这个算法是以距离作为相似度的评价指标，所以不能发现非凸簇集的，时间复杂度也就比较高了。
   （3）.划分完成后，计算每一个类中所有数据点的均值，将该点作为新的中心点。
   （4）.重复2和3当中心点位置变化小于预设阈值，聚类结束。

2. C++代码实现
   代码有参考，点击进入
   在找了许多参考的文章和代码后，这个写的是非常好的，下面是自己理解
   代码第一步将每个坐标的元组准备好：

struct Tuple
{
    float attr1;
    float attr2;
};

计算欧氏距离

float get_XYdis(Tuple t1,Tuple t2)
{
    return sqrt((t1.attr1-t2.attr1)*(t1.attr1-t2.attr1)+(t1.attr2-t2.attr2)*(t1.attr2-t2.attr2));
}

可以根据每个点到各个中心点的距离来确定他是属于哪个簇

int clusteroftulple(Tuple means[],Tuple tupl)
{
    float dis = get_XYdis(means[0],tupl);
    float temp;
    int label=0;
    for(int i=0;i<k;i++)
    {
        temp = get_XYdis(means[i],tupl);
        if(temp < dis)
        {
            dis = temp;
            label = i;
        }
    }
    return label;
}

计算簇集平方误差

float getVar(vector<Tuple>cluster[],Tuple means[])
{
    float var;
    for(int i=0;i<k;i++)
    {
        vector<Tuple> t=cluster[i];
        for(int j=0;j<t.size();j++)
        {
            var += get_XYdis(t[j],means[i]);
        }
    }
    return var;
}

获得当前簇的中心点

Tuple getMeans(vector<Tuple>cluster)
{
    int number = cluster.size();
    double meanX=0,meanY=0;
    Tuple t;
    for(int i=0;i<number;i++)
    {
        meanX += cluster[i].attr1;
        meanY += cluster[i].attr2;
    }
    t.attr1 = meanX/number;
    t.attr2 = meanY/number;
    return t;
}

Kmeans的核心算法

void KMeans(vector<Tuple> tuples)
{
    vector<Tuple>clusters[k];
    Tuple means[k];
    int i=0;
    //默认一开始将前K个元组的值作为K个簇的质心
    for(i=0;i<k;i++)
    {
        means[i].attr1 = tuples[i].attr1;
        means[i].attr2 = tuples[i].attr2;
    }
    int label = 0;
    //根据默认的质心给簇赋值
    for(i=0;i!=tuples.size();++i)
    {
        label = clusteroftulple(means,tuples[i]);
        clusters[label].push_back(tuples[i]);
    }
    //输出刚开始的簇
    for(label=0;label<k;label++)
    {
        cout<< "第" << label+1<<"个簇 : "<<endl;
        vector<Tuple>t =clusters[label];
        for(i=0;i<t.size();i++)
        {
            cout<< "(" << t[i].attr1 << ","<<t[i].attr2<< ")"<< "  ";
        }
        cout<<endl;
    }
    float oldVar =-1;
    float newVar = getVar(clusters,means);
    //当新旧函数值相差不到一时（准则函数值不发生明显变化），算法终止
    while(abs(newVar - oldVar)>=1)
    {
        //更新每个簇中心点
        for(i=0;i<k;i++)
        {
            means[i] = getMeans(clusters[i]);
        }
        oldVar = newVar;
        newVar = getVar(clusters,means);
        //清空每个簇
        for( i=0;i<k;i++)
        {
            clusters[i].clear();
        }
        //根据新的质心获得新的簇
        for(i=0;i!=tuples.size();++i)
        {
            label = clusteroftulple(means,tuples[i]);
            clusters[label].push_back(tuples[i]);
        }
        //输出当前簇
        for(label=0;label<k;label++)
        {
            cout<< "第" << label+1<<"个簇 : "<<endl;
            vector<Tuple>t =clusters[label];
            for(i=0;i<t.size();i++)
            {
                cout<< "(" << t[i].attr1 << ","<<t[i].attr2<< ")"<< "  ";
            }
            cout<<endl;
        }
    }
}

主函数

int main()
{
    char fname[256];
    cout << "请输入文件名 ： ";
    cin >> fname;
    cout<<endl;
    ifstream fin;
    fin.open(fname,ios::in);
    if(!fin)
    {
        cout<<"不能打开文件 : "<<fname<<endl;
        return 0;
    }
    int count = 0;
    vector<Tuple>tuples;
    Tuple tuplee;
    //从文件流中读取数据
    while(!fin.eof())
    {
        count++;
        if(count%2==1)
            fin>>tuplee.attr1;
        else
        {
            fin>>tuplee.attr2;
            tuples.push_back(tuplee);
        }
    }
    //输出文件的元组信息
    for(vector<Tuple>::size_type ix=0;ix!=tuples.size();ix++)
    {
        cout<<"("<<tuples[ix].attr1<< ","<<tuples[ix].attr2<< ")"<< "  ";
    }
    cout<<endl;
    KMeans(tuples);
    return 0;
}

通过验证，可以看到程序是哒到了效果的

3.Matlab实现
首先我们要生成一些需要分类的点，在这里生成三个高斯分布的随机点 data1,data2和data3然后将这些点画出来

clear;
clc;
N = input ('请设置聚类数目 ：');
%% data 1
mu1=[0 0];
s1=[0.1 0;0 0.1];
data1=mvnrnd(mu1,s1,100);
%% data 2
mu2=[-1.25 1.25];
s2=[0.1 0;0 0.1];
data2=mvnrnd(mu2,s2,100);
%% data 3
mu3=[1.25 1.25];
s3=[0.1 0;0 0.1];
data3=mvnrnd(mu3,s3,100);
%% display data scatter
plot(data1(:,1),data1(:,2),'b+');
hold on;
plot(data2(:,1),data2(:,2),'b+');
plot(data3(:,1),data3(:,2),'b+');

在然后进行中心点的初始化工作，定义KMeans算法，给所有的点打上标签

data = [data1;data2;data3];
[m,n]=size(data);
center = zeros(N,n);
pattern = data;
%% Kmeans algorithm
for x = 1:N
    center(x,:)=data(randi(300,1),:);
end
while true
distance = zeros(1,N);
num = zeros(1,N);
new_center = zeros(N,n);
%% 将所有的点打上标签
for x=1:m
    for y=1:N
        distance(y)=norm(data(x,:)-center(y,:));
    end
    [~,temp]=min(distance);
    pattern(x,n+1) = temp;
end;
k=0;

将所有在同一类里的点坐标全部相加，计算新的中心坐标

for y = 1 : N
    for x = 1 : m
        if pattern(x,n + 1) == y
           new_center(y,:) = new_center(y,:) + pattern(x,1:n);
           num(y) = num(y) + 1;
        end
    end
    new_center(y,:) = new_center(y,:) / num(y);
    if norm(new_center(y,:) - center(y,:)) < 0.1
        k = k + 1;
    end
end
if k == N
     break;
else
     center = new_center;
end
end
[m, n] = size(pattern);

最后将聚类后的数据用图片显示出来：

figure;
hold on;
for i = 1 : m
    if pattern(i,n) == 1 
         plot(pattern(i,1),pattern(i,2),'r*');
         plot(center(1,1),center(1,2),'ko');
    elseif pattern(i,n) == 2
         plot(pattern(i,1),pattern(i,2),'g*');
         plot(center(2,1),center(2,2),'ko');
    elseif pattern(i,n) == 3
         plot(pattern(i,1),pattern(i,2),'b*');
         plot(center(3,1),center(3,2),'ko');
    elseif pattern(i,n) == 4
         plot(pattern(i,1),pattern(i,2),'y*');
         plot(center(4,1),center(4,2),'ko');
    else
         plot(pattern(i,1),pattern(i,2),'m*');
         plot(center(5,1),center(5,2),'ko');
    end
end

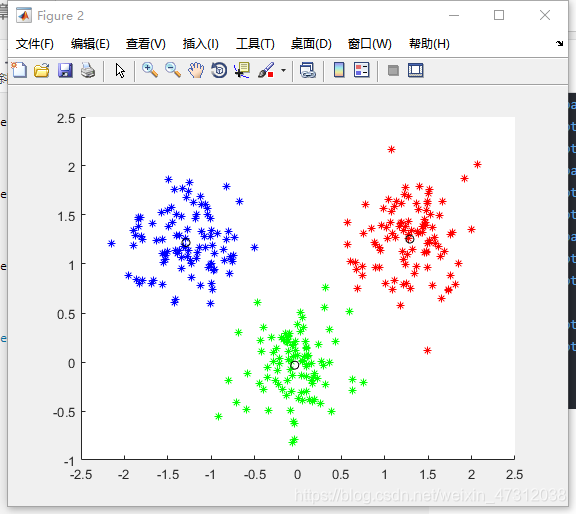
感觉对于这些比较简单的算法直接看代码比去看他的原理分析更能让人接受。