NOIP-2017-J1-真题解析

最新推荐文章于 2025-04-19 13:26:37 发布

原创最新推荐文章于 2025-04-19 13:26:37 发布

· 1.5k 阅读

5 ·

版权

文章标签：

#算法 #数据结构 #二分法

NOIP历年普及组初赛真题解析专栏收录该内容

9 篇文章

订阅专栏

一、选择题

1、B，基础题，考察补码和原码转换，首先符号位是1表示是负数，剩余的位先末尾减1转为反码10101010，然后取反得到原码11010101，转换二进制是-(64+16+4+1)=-85
2、B，基础题，计算机存储基本单位是字节（Byte)
3、C，基础题，考察计算机网络常识，C是世界贸易组织的简称，POP3是Post Office Protocol 3的简称，即邮局协议的第3个版本,它规定怎样将个人计算机连接到Internet的邮件服务器和下载电子邮件的电子协议，SMTP 的全称是“Simple Mail Transfer Protocol”，即简单邮件传输协议，IMAP全称是Internet Mail Access Protocol，即交互式邮件存取协议，它是跟POP3类似邮件访问标准协议之一。
4、A，基础题，考察存储单位换算，一定要算仔细。
$\frac{800*600*16}{8*1024}=937.5KB$
5、A，基础题，考察计算机发展史，计算机应用最早是应用于数值计算。
6、A，基础题，程序设计语言基础，C语言是面向过程语言，C++，Java，C#均是面向对象程序设计语言
7、B，竞赛常识题，NOI中文全称是全国青少年信息学奥林匹克竞赛
8、C，数学题，从2017年往前推到1999年，总共18年，其中2016，2012，2008，2004，2000共5个闰年，其余13个平年，闰年366天，平年365天，总天数对7求余： $(366*5+365*13)\%7=((366\%7)*5+(365\%7)*13)\%7=2$ ，所以将从星期日往前推2天，便是星期五
9、C，数学题，组合数学，甲乙丙三位同学独立选课，分别有 $C_4^2,C_4^3,C_4^3$ ，再根据乘法原理，将三个组合数相乘可得96
10、A，数据结构题，考察树和图的基本知识。n个结点的树，其边数为n-1，所以必须删掉m-(n-1)=m-n+1条边后，才能剩余n-1条边
11、B，数学题，数据量小，根据题意对逆序对的描述，直接枚举可得逆序对有：
(7,2),(7,3),(7,5),(7,4),(5,4)，总共5个
12、B，数据结构题，考察栈在表达式转换的应用，设一个操作数栈和操作符栈，中缀表达式转后缀表达式，从左至右遍历，操作数和操作符依次各自入栈，若遇到右括号，则依次弹出栈顶元素压入操作数栈，直至遇到左括号（两个括号丢弃），其他运算符则跟操作符栈顶元素比较优先级，将栈顶大于其优先级的运算符弹出压如操作数栈，然后将其压入操作符栈，遍历完之后，若操作符栈有剩余，则依次出栈，入操作数栈，最后操作数栈从栈顶逆序输出序列即可。

13、B，数据结构题，考察栈的链式结构，链表的结点插入操作，栈只能从栈顶插入，所以要从链表头部插入结点s指向的结点，将s变成栈顶指针，s指向的结点变成栈顶结点。

14、C，数学题，依次枚举，注意不要漏掉空串，非空子串有1+2+…+9=45，然后加上空串，总共46个
15、A，基础题，进制转换，整数部分依次除2，余数序列逆序输出可得，小数部分依次乘以2，取整数部分，小数部分继续乘以2，取整数部分，直至最后小数部分为0，结果序列顺序输出可得。

16、C，数据结构题，考察栈的合法出栈序列，依次检测每个选项，C中，b，c在d后面出栈，那么d出栈时，栈顶只能是c，所以d后面c一定要比b先出栈，故C不对
17、D，算法题，考察归并排序算法，最好情况下，是两个序列刚好可以首尾相连，需要n次比较，最坏的情况是每次比较交替取A和B序列中的1个元素放入合并序列，反过来思考，合并序列有2n个元素，除了最后一个，前面的2n-1个每个都需要经过1次比较获得，最后一个不需比较，直接放到最后一个位置即可，所以最坏情况是2n-1次比较
18、B，竞赛常识题，2022年开始，NOIP将不再支持Pascal语言
19、C，数学题，考察概率基础，排除法，首先求任意两人生日都不同的概率，然后1减之即可
$1-\frac{12*11*10*9}{12*12*12*12}=\frac{41}{96}$

20、B，基础题，计算机发展史，图灵奖是计算机领域最高荣誉奖项

二、问题求解

1、数学题，首先看步数n，从第1象限开始顺时针开始，依次将每个象限记为区域1，2，3，4，每4步一个轮回，n%4=1，2，3，0依次落在区域1，2，3，4，2017%4=1，所以比如落在区域1，然后观察区域1的点，相邻两个点，后面的点的坐标均比前面的点增加2，2017/4=504，所以坐标是在第1个点的基础上横坐标，纵坐标分别加上 $504 * 2$ 即可
$x = 1 + 504 * 2 = 1009, y = 0 + 504 * 2 = 1008$

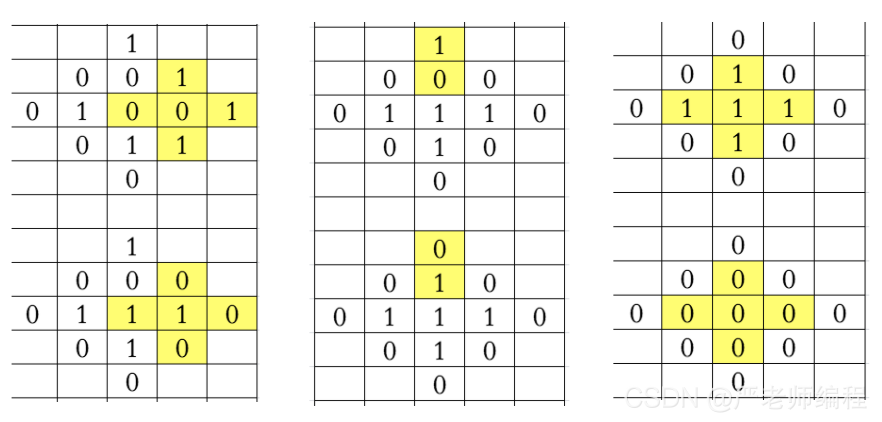
2、首先选周边1最多的十字进行操作变换即可，如下图所示，总共3次操作

三、阅读程序

1、

#include<iostream>
using namespace std;
int main()
{
    int t[256];
    string s;
    int i;
    cin >> s;
    for (i = 0; i < 256; i++)
        t[i] = 0;
    for (i = 0; i < s.length(); i++)
        t[s[i]]++;
    for (i = 0; i < s.length(); i++)
        if (t[s[i]] == 1)
        {
            cout << s[i] << endl;
            return 0;
        }
    cout << "no" << endl;
    return 0;
}

输入：xyzxyw
编程题，考察字符串处理，输入的字符串s=“xyzxyw”，t数组按照类似桶排序的方式，统计s中不同字符出现的次数，最后统计结果是t[‘x’]=2,t[‘y’]=2,t[‘w’]=1,t[‘z’]=1，然后遍历s，找到第一个出现1次的字符，就将其输出，程序返回，显然第一个找到的是s的第3个字符z，t[‘z’]=1，所以结果输出为z

2、

#include<iostream>
using namespace std;
int g(int m, int n, int x)
{
    int ans = 0;
    int i;
    if (n == 1)
        return 1;
    for (i = x; i <= m / n; i++)
        ans += g(m - i, n - 1, i);
    return ans;
}
int main()
{
    int t, m, n;
    cin >> m >> n;
    cout << g(m, n, 0) << endl;
    return 0;
}

输入：7 3
编程题，考察递归求解，直接根据代码逻辑，自顶向下画出递归树，n=1时即为叶子节点，直接返回1，然后自底向上合并返回，可得结果为8

3、

#include<iostream>
using namespace std;
int main()
{
    string ch;
    int a[200];
    int b[200];
    int n, i, t, res;
    cin >> ch;
    n = ch.length();
    for (i = 0; i < 200; i++)
        b[i] = 0;
    for (i = 1; i <= n; i++)
    {
        a[i] = ch[i - 1] - '0';
        b[i] = b[i - 1] + a[i];
    }
    res = b[n];
    t = 0;
    for (i = n; i > 0; i--)
    {
        if (a[i] == 0)
            t++;
        if (b[i - 1] + t < res)
            res = b[i - 1] + t;
    }
    cout << res << endl;
    return 0;
}

输入：1001101011001101101011110001
编程题，考察字符串处理，数组，循环语句，程序阅读跟踪能力，这类题型，最好是打表，仔细跟踪程序，列出相关数组和变量的值，如下图所示，先分别列出ch, a, b3个数组元素，然后res初值=b[n]=16，从后往前遍历数组，更新res，最后res值为11
在这里插入图片描述
4、

#include<iostream>
using namespace std;
int main()
{
    int n, m;
    cin >> n >> m;
    int x = 1;
    int y = 1;
    int dx = 1;
    int dy = 1;
    int cnt = 0;
    while (cnt != 2)
    {
        cnt = 0;
        x = x + dx;
        y = y + dy;
        if (x == 1 || x == n)
        {
            ++cnt;
            dx = -dx;
        }
        if (y == 1 || y == m)
        {
            ++cnt;
            dy = -dy;
        }
    }
    cout << x << " " << y << endl;
    return 0;
}

编程题，考察数组的周期变化，while循环里每次循环x,y各自添加增量dx, dy，初始都是加1，然后每当x累加到最大值m，或y累加到最大值n，dx，dy符号取反，x,y开始逐步变小，当减小到最小值1时，dx, dy符号再取反，x,y又开始逐步增加复原，如此周期进行，循环退出的条件是cnt==2，即某次x，y同时达到极值的时候，退出，然后输出此刻的x，y。
第1空，x,y初值为4，3，如下图所示，当x经历1-4-1，y经历1-3-1-3，x,y同时达到极值，输出1，3
第2空，同理可得，x经历1-2017，y经历1-1014-1，x,y同时达到极值，输出2017，1
在这里插入图片描述

四、完善程序

1、在这里插入图片描述

#include<iostream>
using namespace std;
int x, p, m, i, result;
int main(){
    cin >> x >> p >> m;
    result = ①;
    while (②){
        if (p % 2 == 1)
            result = ③;
        p /= 2;
        x = ④;
    }
    cout << ⑤ << endl;
    return 0;
}

算法题，考察分治法和余数乘法定理的应用。首先①应该是1，result是结果，在计算过程中是累乘的，所以初值必然是1，⑤是输出结果，必然是result。
根据余数乘法定理： $(a * b) m o d m = (a m o d m) * (b m o d m) m o d m$
结合快速幂，不断将指数P二分，从 $x^2$ 开始计算，直到达到 $x^p$ ，特别地当p是奇数的时候，单独分一个x出来，剩余的p-1次幂再二分计算，所以③是 $result*x\%m$ ，④是 $x*x\%m$ ，每次x翻一番，②是p!=0或p>0或p，因为是通过不断将p除2来循环的，所以直到p除尽变为0的时候退出循环。

2、完善程序（切割绳子）有 n 条绳子，每条绳子的长度已知且均为正整数。绳子可以以任意正整数长度切割，但不可以连接。现在要从这些绳子中切割出 m 条长度相同的绳段，求绳段的最大长度是多少。（第一、二空 2.5 分，其余 3 分）
输入：第一行是一个不超过 100 的正整数 n，第二行是 n 个不超过10^6
的正整数，表示每条绳子的长度，第三行是一个不超过10^8的正整数 m。输出：绳段的最大长度，若无法切割，输出 Failed

#include<iostream>
using namespace std;
int n, m, i, lbound, ubound, mid, count;
int len[100]; // 绳子长度
int main()
{
    cin >> n;
    count = 0;
    for (i = 0; i < n; i++)
    {
        cin >> len[i];
        ①;
    }
    cin >> m;
    if (②)
    {
        cout << "Failed" << endl;
        return 0;
    }
    lbound = 1;
    ubound = 1000000;
    while (③)
    {
        mid = ④;
        count = 0;
        for (i = 0; i < n; i++)
            ⑤;
        if (count < m)
            ubound = mid - 1;
        else
            lbound = mid;
    }
    cout << lbound << endl;
    return 0;
}

算法题，考察二分法的应用。阅读题目，绳子只能以任意正整数切割，切割得到的m条长度相等的绳子，显然m越大，则其长度越小，m越小，则其长度越大。m最小是1，其长度是原n条绳子中最长的的那条，即不用切割，m条绳子的最小长度是1，此时m最大，m条绳子的总长度是m*1=m，那m必须小于等于原n条绳子的总长度之和，否则无法切割，对应代码中输出Faild的条件。
①count+=len[i]，是累计n条绳子长度总和，②count<m，则是无法切割时成立的条件，即m超过了n条绳子长度总和，此时无法切割，输出Failed，程序结束。
否则，接下来在满足能切割的前提下，开始用二分法进行查找，前面确定了m条绳子的长度最小是lbound=1，最大是原绳子的最大长度ubound=10^6，在此范围进行二分查找，找到一个最大的满足切割条件的绳子长度。
③lbound<ubound，二分边界查找的循环条件，查找区间是左闭右开[lbound, ubound)，循环终止条件是lbound==ubound，这个根据后面代码的区间划分可以得出，④mid=(lbound+ubound)/2+1，mid表示当前试探的切割长度，然后⑤count+=len[i]/mid，就是检测按当前mid长度进行切割每条绳子所得的绳子总条数是否达到m条，如果达不到m条，则表示切割长度取大了，则要在左边小区间[lbound, mid-1)里再进行二分查找，否则表示，切割长度取小了，还有可能切割的更大一些，则要在右边区间[mid, ubound)里进行二分查找，这样不断进行二分查找，直到找到一个最大的满足能切割出m条长度相同的绳子的切割长度，最终满足条件的时候lbound=ubound，所以最终输出lboud即可。

此题需要注意的是④mid=(lbound+ubound)/2+1，为何要加1，而不是直接mid=(lbound+ubound)/2，是因为代码给出的当count<m不成立的时候，lbound=mid，而不是lound=mid+1，分析一下，如果当lbound和ubound相邻的时候，mid=(lbound+ubound)/2=lbound，当count>=m时，将lbound更新为mid，其实等于是没有更新，lbound和ubound都不会变，下一轮循环将进入死循环，所以需要将mid=(lbound+ubound)/2+1=ubound，这样当count>=m时，lbound更新为ubound，这样下次循环条件lounb<ubound就不成立了，循环正常退出，得到结果。