【线段树】一文搞懂线段树 ！！！（超详细解析）

于 2024-05-01 14:31:54 发布
阅读量267 收藏 24
点赞数 25
CC 4.0 BY-SA版权
文章标签： 算法 线段树
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/weixin_46879314/article/details/138372007
本文详细介绍了线段树的基本概念、结构以及如何利用递归实现区间和的计算。重点讲解了区间增加、更新和查询的操作原理，以及如何通过懒更新优化时间复杂度至O(logN)。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

点击下载本文源码

线段树 中使用了大量的 二叉树递归 操作。

如果对于二叉树的 递归套路 不熟的小伙伴可以关注（同名），在主页 「二叉树」 合集里查看哦 ~

也可以点击两篇文章链接直达:

“一套逻辑” 搞定所有二叉树性质题

“一套逻辑”搞定二叉树 - 2！

这里简单回顾一下 套路总结（该总结在第二篇文末哦~）：

接下来进入正题 （点击下载本文源码）：

---------------------------长文警告-------------------------

线段树

线段树 是一种特殊的 二叉搜索树，每个结点 存储一个区间，或理解为一个线段，可以在这些区间上进行相应的操作。

因此，线段树数组 中保存的是某个区间 [L,R] 上的某种信息，例如 区间和、区间最大值、区间最小值 等等。

注意： 线段树数组中一般从下标 1 处开始存储数据，0 号位置舍弃不用。

如下图所示，树的每个结点保存的某个区间范围的信息。可以发现，叶子结点 的区间长度仅为 1 ，父结点 保存的是左右孩子区间合并之后的区间信息。由此，构建了一棵二叉搜索树。

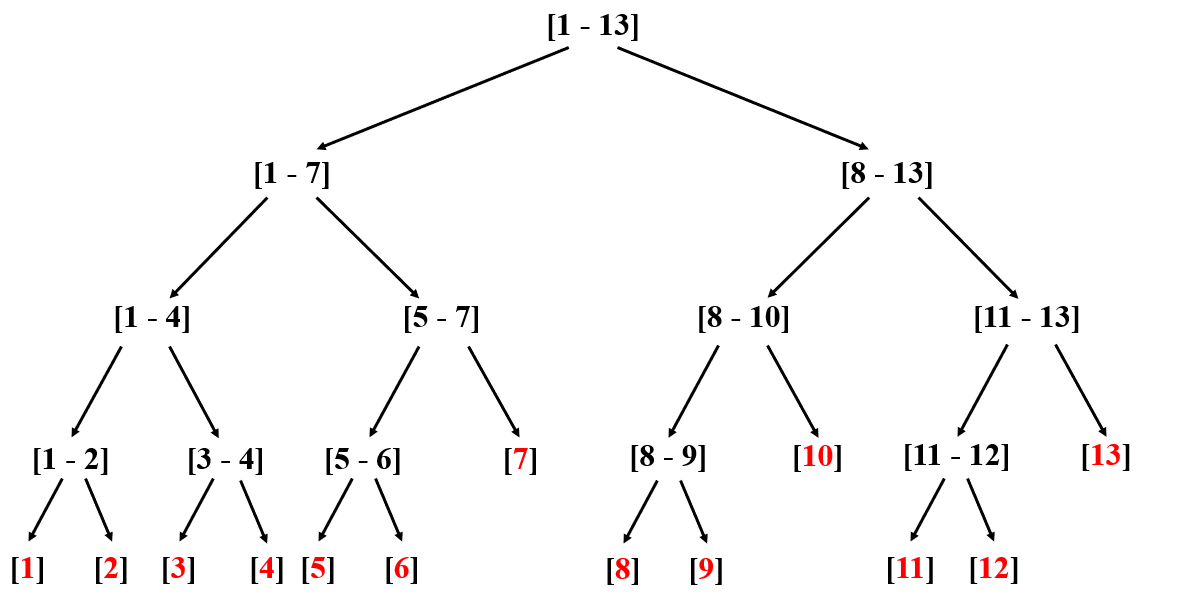
举两个🌰🌰：

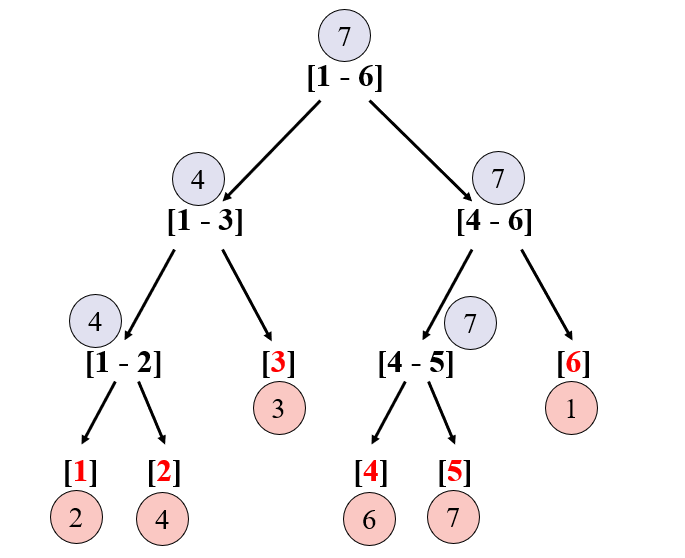
例1. 数组 a[6]={2,4,3,6,7,1}，求 区间最大值 的线段树表示为：

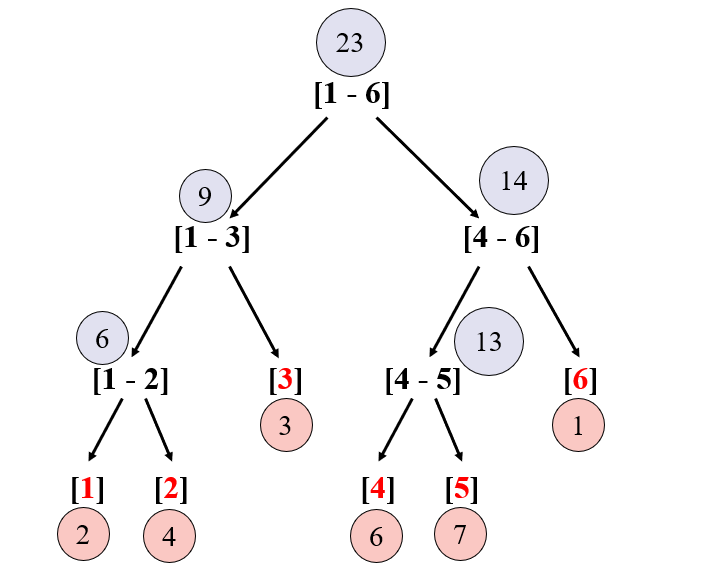
例2. 数组 a[6]={2,4,3,6,7,1}，求 区间和 的线段树表示为：

父结点和子结点的下标关系为：

线段树中保存的是圆圈中的信息哦，那思考一下，存储这些信息需要多大的存储空间呢？

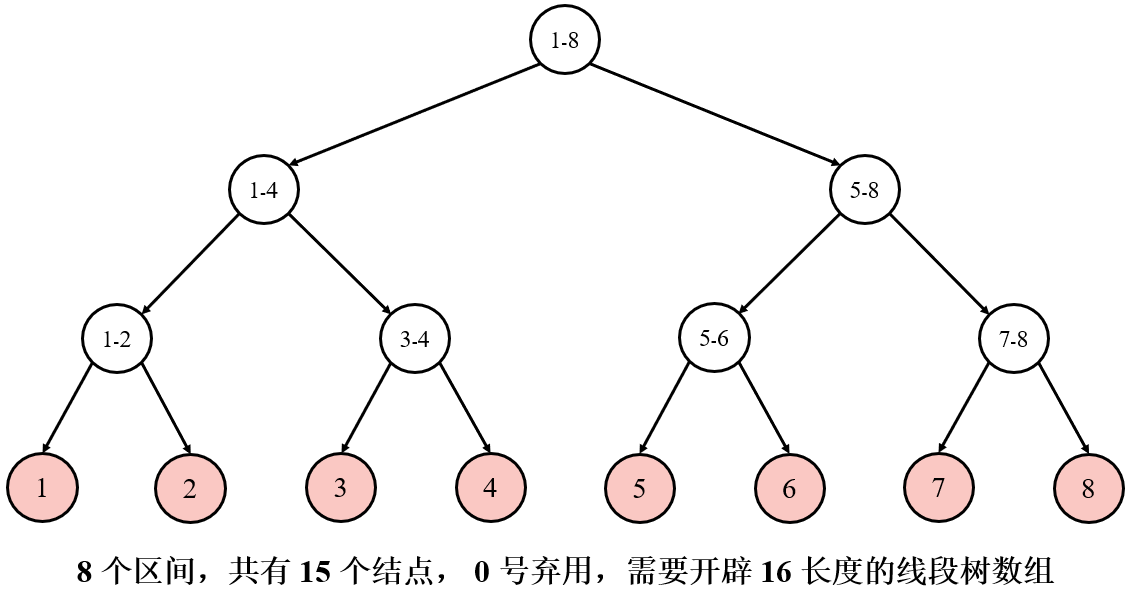
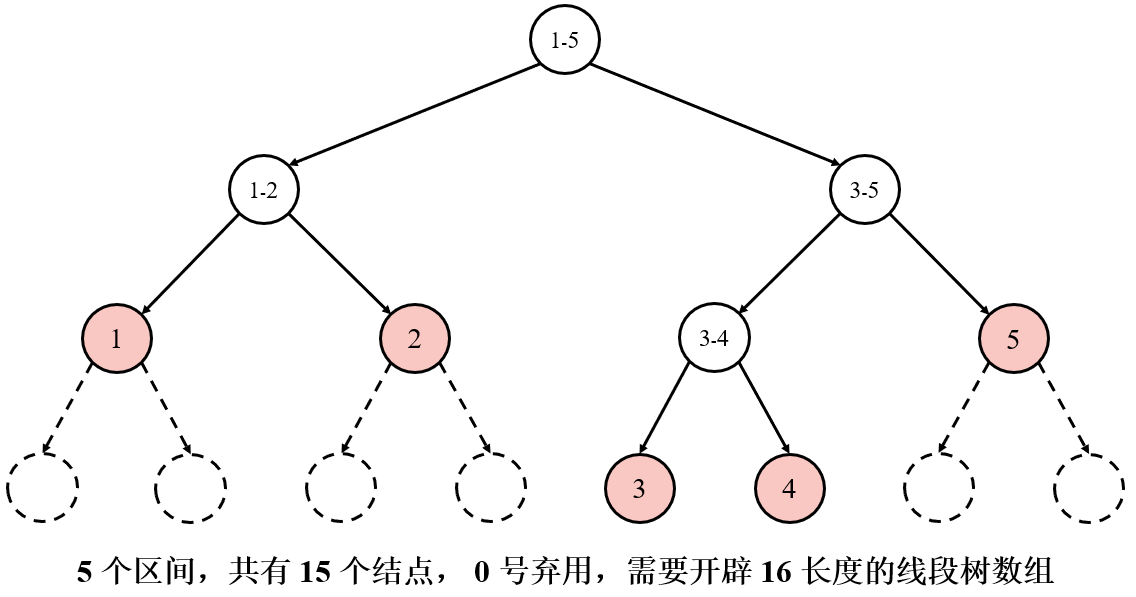
结论：

因此，为防止空间不足，会将线段树的数组空间统一开辟 4 n 4n 4n 大小。

以上我们介绍完了线段树最基本的特征。

现在有几种需求：

  1. 对数组中某个连续区间内的所有元素进行统一的 加 操作；
  2. 对数组中某个连续区间内的所有元素进行统一的 更新 操作；

看完两种操作，是不是很容易就能想到遍历数组呢？的确。但遍历数组的时间复杂度为 O ( N ) O(N) O(N) ，线段树却能够做到 O ( l o g N ) O(logN) O(logN) 级别。

为了完成以上两种操作，需要先建立出所给数组对应的线段树，以下均以 区间求和 的业务逻辑为例进行示例。

建树代码

public static class SegmentTreeClass {
    private int MAXN;
    // 原数组，下标从 1 开始存储
    private int[] arr;
    // 区间和的线段树数组
    private int[] sum;
    // 懒更新数组，区间加 时用到
    private int[] lazy;
    // 更新数组，区间更改 时用到
    private int[] change;
    // 更新标记，区间更改 时用到
    private boolean[] update;

    // 初始化
    public SegmentTreeClass(int[] origin) {
        MAXN = origin.length + 1;
        arr = new int[MAXN];
        // 复制数组，从 1 开始
        for (int i = 1; i < MAXN; i++) {
            arr[i] = origin[i - 1];
        }
        sum = new int[MAXN << 2];
        lazy = new int[MAXN << 2];
        change = new int[MAXN << 2];
        update = new boolean[MAXN << 2];
    }

    // 父结点区间 = 左右孩子结点区间之和
    private void pushUp(int rt) {
        sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
    }

    public void build(int l, int r, int rt) {
        // 叶结点
        if (l == r) {
            sum[rt] = arr[l];
            return;
        }
        // 求中间区间，递归调用
        int mid = (l + r) >> 1;
        build(l, mid, rt << 1);
        build(mid + 1, r, rt << 1 | 1);
        // 整合左右孩子
        pushUp(rt);
    }

}

建树代码解释

  1. 为了方便，线段树下标从 1 开始，拷贝一份原始数组。初始化时，每个数组大小均开 4 n 4n 4n 的大小。
  2. 由于业务逻辑为 区间的累加和。根据线段树的特点，父结点存储的是左右两个子结点区间的总和。因此，pushUp() 函数对左右两个孩子的 sum 数组进行累加，即可得到父结点的 sum[rt] 值。
  3. 递归函数 build() 就是简单的 二叉树递归套路 。basecase 为区间长度为 1 时，sum 数组即为 arr 数组的值。左右两个孩子的信息得到后，即可合并得到父结点 sum[rt] 的值。

到这里，整棵线段树就建立好了。

接下来，我们对上面提到的几种需求进行讨论。

需求1：区间增加

需求描述： add[L,R,C] 表示给某个连续的区间[L,R]范围内的所有值都加一个定值 C。

lazy[] 懒标记数组规则：

  1. 如果 想要更新的目标区间 完全包裹住了 此时 该下标所在结点的区间范围，使用懒数组进行标记，并且不再向下传递更新。

  2. 如果没有被包裹住，则向下（左右两个孩子）分发，直到被包裹住后停止下发。

  3. 只有当新的操作也来到该结点时，被标记的懒数组只向下更新一层（传递给左右孩子）。（请参考下面 pushDown()函数中 lazy[rt]!=0代码部分）

  4. 该方法无需每次更新到叶子结点，减少大量操作，复杂度优化到了 O ( l o g N ) O(logN) O(logN) 。

没看懂规则，没关系，看图：

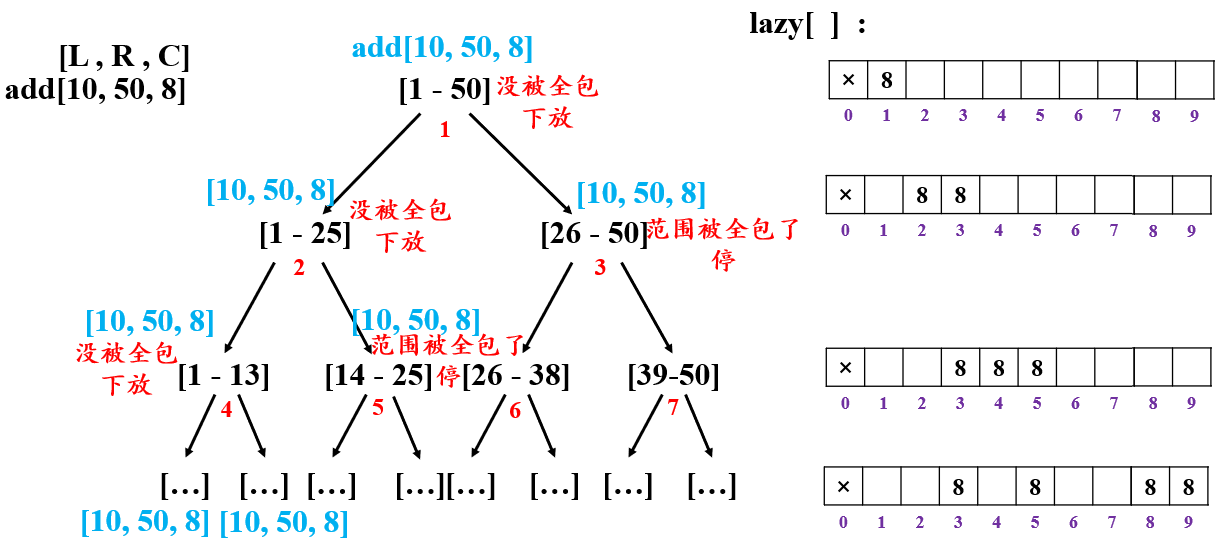
解释:

  1. 现有 1-50 的线段树，现要让 10~50 范围上的每个数增加 8 。

  2. 首先来到下标为 1 的[1,50]结点，因此，lazy[1]=8。由于[1,50]不全在10~50范围内，所以只能下放。

  3. 下放的结果是lazy[2]=8 和 lazy[3]=8。由于lazy[3]对应范围是[26,50]，全部都在10~50范围内，不再下放。lazy[2]范围是[1,25]，不符合范围，所以继续下放。

  4. lazy[2]下放到lazy[4],[5]。lazy[5]全包了，不再下放，lazy[4]继续下放到lazy[8][9]…，直到全部包裹住后，停。

  5. 当下放到某个结点处停止后，需要及时更新此时的sum[]和lazy[]数组。

加数代码

// L~R 范围内均 +C
// 此时来到了 l~r 范围，该结点为 rt
public void add(int L, int R, int C, int l, int r, int rt) {
    // 全包住了
    if (L <= l && R >= r) {
        // 该范围内全部的数都要+C
        // 所以该结点的 sum 值就会增大 C*(r-l+1)
        sum[rt] += C * (r - l + 1);
        // 不再往下发，在 rt 这里停住了，懒数组值 +C
        lazy[rt] += C;
        return;
    }
    // 没全包住，递归往下发
    int mid = (l + r) >> 1;
    // 如果之前有懒信息，先发下去
    pushDown(rt, mid - l + 1, r - mid);
    // 左边没包住，往左 下发
    if (L <= mid) {
        add(L, R, C, l, mid, rt << 1);
    }
    // 右边没包住，往右 下发
    if (R > mid) {
        add(L, R, C, mid + 1, r, rt << 1 | 1);
    }
    // 左右都完成了，合并
    pushUp(rt);
}

// 下放一层
public void pushDown(int rt, int ln, int rn) {
    if (update[rt]) {
        // 后面再补充
    }
    // 懒信息不为 0，下放给左右孩子
    if (lazy[rt] != 0) {
        // 更新左孩子的 lazy和sum数组
        lazy[rt << 1] += lazy[rt];
        sum[rt << 1] += lazy[rt] * ln;
        // 更新右孩子的 lazy和sum数组
        lazy[rt << 1 | 1] += lazy[rt];
        sum[rt << 1 | 1] += lazy[rt] * rn;
        // 下放给孩子了，自己要清零
        lazy[rt] = 0;
    }
}

add()函数总结

  • 如果新到的结点有懒信息，先下发一层，自己清空（pushDown函数）；
  • 无懒信息时（add函数）：
    • 如果区间全部包裹住了，不再下发，更新 sum 和 lazy 数组；
    • 区间没包裹住，根据区间往左右孩子下发，最后再合并（递归部分的代码）。

需求2：区间更新

需求描述： update[L,R,C] 表示把某个连续的区间[L,R]范围内的所有值都更改为 C。

change[] 更新数组规则：

  1. 如果 想要更改的目标区间 完全包裹住了 此时 该下标所在结点的区间范围，不再向下传递更新，直接设置change[rt]=C，更新sum[rt]并将lazy[rt]置为 0 （即便之前有懒信息，都 被 change 覆盖掉 了）。

  2. 如果没有被包裹住，如果当前结点在之前有更新信息，需要先下发给左右孩子，即调用pushDown()函数中update[rt]代码部分。注意在更新change的同时，lazy数组置零，并修改sum的值（理由同 1 ，被覆盖掉了）。

  3. 无以前的更新信息后，递归调用，最后整合即可。

update[] 作用：

  1. 由于数组默认值为 0 ，如果更新值也恰好为 0 ，会产生混淆。

  2. 使用update[]进行标记，只有为 true 的值才为真正要更新的值。

更新代码

// L~R 范围内均更新为 C
// 此时来到了 l~r 范围，该结点为 rt
public void update(int L, int R, int C, int l, int r, int rt) {
    // 全包住了
    if (L <= l && R >= r) {
        // 确认要更新
        update[rt] = true;
        // 更新为 C
        change[rt] = C;
        // 修改 sum 的值为 C * (r - l + 1)
        sum[rt] = C * (r - l + 1);
        // 懒信息被覆盖掉了，清空
        lazy[rt] = 0;
        return;
    }
    // 没全包住，递归往下发
    int mid = (l + r) >> 1;
    // 之前有更新信息，先下发
    pushDown(rt, mid - l + 1, r - mid);
    // 左边没包住，往左 下发
    if (L <= mid) {
        update(L, R, C, l, mid, rt << 1);
    }
    // 右边没包住，往右 下发
    if (R > mid) {
        update(L, R, C, mid + 1, r, rt << 1 | 1);
    }
    // 整合
    pushUp(rt);
}

public void pushDown(int rt, int ln, int rn) {
    // 有更新信息先处理
    if (update[rt]) {
        // 更新左右孩子的 更新信息
        update[rt << 1] = true;
        change[rt << 1] = change[rt];
        update[rt << 1 | 1] = true;
        change[rt << 1 | 1] = change[rt];
        // 修改左右孩子的 懒信息
        lazy[rt << 1] = 0;
        sum[rt << 1] = change[rt] * ln;
        lazy[rt << 1 | 1] = 0;
        sum[rt << 1 | 1] = change[rt] * rn;
        // 更新过了，就置为 false
        update[rt] = false;
    }
    // 之前出现过了
    if (lazy[rt] != 0) {
        lazy[rt << 1] += lazy[rt];
        sum[rt << 1] += lazy[rt] * ln;
        lazy[rt << 1 | 1] += lazy[rt];
        sum[rt << 1 | 1] += lazy[rt] * rn;
        lazy[rt] = 0;
    }
}

update()函数总结

  • 结点在之前有更新信息，先下发一层（pushDown函数）；
  • 无懒信息时（update函数）：
    • 如果区间全部包裹住了，不再下发，更新 change 和 update 数组，并修改 sum 和 lazy 数组信息。
    • 区间没包裹住，根据区间往左右孩子下发，最后再合并（递归部分的代码）。

最后一个啦~

需求3：区间累加和

需求描述： query[L,R] 返回某个连续的区间[L,R]范围内的所有值的累加和（即区间值的 查询操作）。

有了前两个的基础，该需求代码很容易看懂了 ~ 直接给出代码

查询代码

public long query(int L, int R, int l, int r, int rt) {
    // 全包直接返回 sum
    if (L <= l && R >= r) {
        return sum[rt];
    }
    int mid = (l + r) >> 1;
    // 先下发
    pushDown(rt, mid - l + 1, r - mid);
    // 再递归
    long ans = 0;
    if (L <= mid) {
        ans += query(L, R, l, mid, rt << 1);
    }
    if (R > mid) {
        ans += query(L, R, mid + 1, r, rt << 1 | 1);
    }
    return ans;
}

总结

以上，我们通过构建线段树，实现了在 O ( l o g N ) O(logN) O(logN) 的时间复杂度内，完成对 任意区间 的 增加、修改、查询 操作。

注意： 以上构建线段树是以 求区间和 为业务逻辑的，不同题目需要根据具体要求更改线段树的构建方式。

本文超级长，思维量也足够大，能够看到这里的小伙伴们不容易！！！

代码量很大，完整代码（含测试）关注回复关键字「线段树」
或点击链接即可下载

~ ~ ~ 完结撒花 ~ ~ ~

关注
回复「ACM紫书」获取 ACM 算法书籍 ~
回复「算法导论」获取 算法导论第3版 ~

在看 + 转发

让你的小伙伴们一起来学算法吧！！

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

强连通子图

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值