绳子最多覆盖点问题：长度为k的绳子能覆盖数组arr中最多的点数是多少

绳子最多覆盖点问题：长度为k的绳子能覆盖数组arr中最多的点数是多少？

提示：窗口法：专门解决单调性问题，经常用来处理子数组达标的情况的问题

窗口法解决问题的案例基础：
【1】数组累加和三连1：arr全大于0，请问累加和为k的子数组最大长度是多少
【2】求字符串s涵盖字符t中所有字符的最小子串长度
【3】二分法查找有序数组arr中，大于等于k的最左侧、最右侧的位置

---

题目

给定有序数组 arr，从左往右arr[i]代表坐标轴上的位置，
给定一个整数k，返回：
若有一根绳子长为k，这根绳子能覆盖arr上最多的点数是多少？
（绳子边缘在arr上也算覆盖，边界点也是覆盖）

---

一、审题

示例：arr=1 5 7 13 14
k=5

从左往右滑动绳子，长k=5
最开始1–5,2个点
然后5–7,2个点
然后13 14，2个点
所以最多覆盖2个

---

案例说的就是暴力解o(n^2)，以每个j为开头，看看绳子能覆盖到最远的i位置，i-j+1即覆盖点数

0位置是起点，N-1位置终点
中间每一个j位置，做绳子的出发点，看看绳子能延伸到最远的位置i，则长度就是i-j+1，不断更新就能搞定。

这种方法，暴力，j的取值有N种
每次从j–i索引i，又是o(n)
故算法复杂度为o(n^2)

不可取，需要优化

---

优化解1：二分查找：o(nlog(n))，比暴力解好多了，仍不是最优解

怎么做呢？
长度为k的绳子，我们以每一个i为绳子覆盖的结尾点
则能覆盖到的起点j处，arr[j]就是L=arr[i]-k

如果我们在arr的0–i-1之间去二分查找>=L的最左那个j位置，则
覆盖点数就是：i-j+1
每一个i位置更新一次max，最后答案必在其中

重要的基础知识：在arr的L–R范围之间去二分查找>=L的最左那个j位置
此前咱们就学过的基础，老早就会了
看基础知识文章：
【3】二分法查找有序数组arr中，大于等于k的最左侧、最右侧的位置

看完你就知道代码怎么写了，也很简单，二分查找，在arr的L–R范围之间去二分查找>=L的最左那个j位置，不断逼近最左边那个地方
之所以要找大于等于L的元素arrmid（其位置是j位置），是因为只有arrmid大于等于k，arri-arrmid才能小于等于绳子长度，达到覆盖的目的

手撕这个代码：

    //复习：
    //二分查找>=k的最左侧那个位置j
    public static int moreThankMostLeftPos(int[] arr, int L, int R, int k){

        int j = -1;//默认没有找到

        while (L <= R){
            int mid = L + ((R - L) >> 1);
            if (arr[mid] >= k){//arr中，大于等于k的最左那个元素的位置j
                //arrmid大于等于k，arri-arrmid才能小于等于绳子长度，达到覆盖的目的
                j = mid;//先记录，往左逼
                R = mid - 1;
            }else L = mid + 1;
        }

        return j;//j=-1的话，i就是覆盖点数
    }

函数返回的j一定不是-1，因为>=L=arr[i]-k的最左位置，最次也是arr[i]

然后主函数，直接来到i位置调用上面这个函数，搞到j位置就可以更新答案了
测试一把：

    public static int maxPointReview1(int[] arr, int k){
        if (arr == null || arr.length == 0 || k <= 0) return 0;

        int max = 1;//至少一个点的
        int N = arr.length;
        for (int i = 1; i < N; i++) {
            //>=arr[i] - k的最左侧那个位置j，是绳子覆盖最远的起点
            int j = moreThankMostLeftPos(arr, 0, i - 1, arr[i] - k);
            max = Math.max(max, i - j + 1);//j不会是-1，一定有>=arr[i] - k的元素，大不了就是arr[i]
        }

        return max;
    }

    public static void test(){
        int[] arr = {1,3,5,7,9,13,14};
        int Len = 5;
        System.out.println(maxPoint1(arr, Len));
        System.out.println(maxPoint2(arr, Len));
        System.out.println(maxPointReview1(arr, Len));
    }

    public static void main(String[] args) {
        test();
    }

问题不大：

3
3
3

你看看外围每一个i位置调度o(n)
内部每次寻找>=arr[i]-k的最左那个位置j需要的时间是o(log(n)）二分法呗
故整体复杂度为o(nlog(n))，比暴力解快多了吧！

---

最优解：窗口法，L–R使劲扩最大绳子长度，R-L就是覆盖点数

涉及数组的事情，还有给定问题是求一个范围上的事情，要么是区间操作（线段树），要么是范围上的达标情况（窗口问题）
这种时候，咱们见太多了，大多为了加速，都要采取双指针窗口控制法
以每个i位置做一次窗口的起点，然后扩k这么长的窗口，就是绳子，看看窗口能覆盖最多点数是多少？
比如来到i位置，当L，起点，咱们使劲扩，只要R不越界，arr[R]-arr[L]<=k的话，就让R到绳子最远的地方：
期初刚刚到绳子k最右端时，R刚刚合适

再扩一下，R=R+1，此时arr[R]-arr[L]>k了，这是绳子没法覆盖了
就收集更新答案：覆盖点数就是R-L

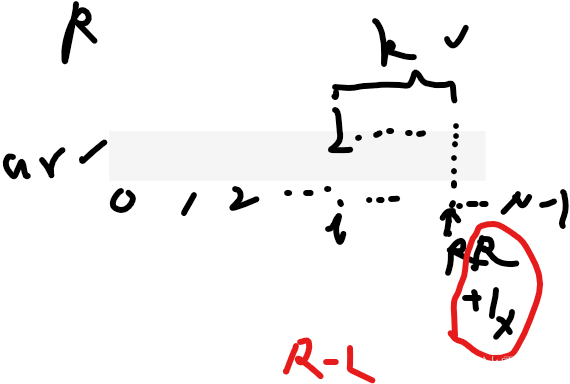
这个窗口只会沿着arr滑动一遍，所以复杂度**o(n)**搞定

手撕代码瞅瞅：

    //复习：比如来到i位置，当L，起点，咱们使劲扩，**只要R不越界，arr[R]-arr[L]<=k的话**，就让R到绳子最远的地方：
    public static int maxPointReview2(int[] arr, int k){
        if (arr == null || arr.length == 0 || k <= 0) return 0;
        int N = arr.length;

        int L = 0;//默认i=0是起点，每一个i位置做一次L，去查
        int R = 0;
        int max = 1;
        while (L <= R){
            while (R < N && arr[R] - arr[L] <= k) R++;//扩窗口
            //扩不动了，R刚刚不算，更新然后动L，探索N个i位置
            max = Math.max(max, R - L);
            L++;
        }

        return max;
    }

测试一下：

   public static void test(){
        int[] arr = {1,3,5,7,9,13,14};
        int Len = 5;
        System.out.println(maxPoint1(arr, Len));
        System.out.println(maxPoint2(arr, Len));
        System.out.println(maxPointReview1(arr, Len));
        System.out.println(maxPointReview2(arr, Len));
    }

    public static void main(String[] args) {
        test();
    }

问题不大

3
3
3
3

如何，速度够快吧！

---

总结

提示：重要经验：

1）涉及数组的事情，还有给定问题是求一个范围上的事情，要么是区间操作，要么是范围上的达标情况
这总时候，咱们见太多了，大多数为了加速，都要采取双指针窗口控制法
2）窗口法一定要在碰到数组时尝试用用，o(n)一遍过，速度快。
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。