Morris遍历：与二叉树的递归遍历（DFS/BFS）不同，优化空间复杂度为o(1)

Morris遍历：与二叉树的递归遍历（DFS/BFS）不同，优化空间复杂度为o(1)

提示：本节来说二叉树的Morris遍历，面试的高超优化技能！

此前学的关于二叉树的概念，先序遍历，中序遍历，后续遍历（这仨统称DFS遍历）和按层的方式遍历（俗称BFS遍历）重要的基础知识：
【1】二叉树，二叉树的归先序遍历，中序遍历，后序遍历，递归和非递归实现
【2】二叉树的宽度优先遍历BFS：按层的遍历方式，请你用队列实现DFS，或者请你用栈实现BFS
【3】求二叉树中，包含的最大二叉搜索子树的头节点是谁，它包含的节点数量是多少

这仨文章，都是重要的基础知识，笔试的时候可以用
面试的时候，除了上面仨，咱们还可以说一下Morris遍历的优化技能

---

题目

Morris序是啥？Morris遍历的流程你会吗？

---

Morris遍历流程，Morris序

其实Morris遍历目的就是为了节约空间，比如上面的如何判断二叉树是否为搜索二叉树
你完全可以整一个中序遍历，把所有元素value放入数组arr中，再判断arr是否是为整体升序？
一旦i-1位置有一个大于i位置的情况，必然不是搜索二叉树。

那个题目，会浪费一定得arr空间，那能不浪费空间，搞定这件事吗？
当然，之前咱们学了树形DP，收集树的信息Info，然后玩树形DP的递归套路，也是可以的，但是那代码复杂，信息复杂
没Morris遍历来得简洁，只要你会Morris遍历的流程，记住了基础代码，实际上破解这题目，非常容易，微微改编一下就行。

OK，下面咱们来说Morris遍历的流程，很容易，学会了之后，自己捋清楚，就能记住

Morris遍历的流程：
（0）cur默认最开始指向head，mR默认为null【即cur左树的最右节点】，判断cur是否有左树？
（1）cur如果没有左树，直接去右树cur=cur.right（当然没有右树那停止Morris遍历）
（2）cur如果有左树，先找到左树的最右节点mR
（3）如果（2）中mR.right=null，则让mR.right=cur，cur=cur.left
（4）如果（2）中mR.right=cur,则让mR.right=null，然后cur=cur.right

就这么一个流程
咱们举个例子说明：
（0）cur默认最开始指向head，mR默认为null【即cur左树的最右节点】，判断cur是否有左树？
（2）cur如果有左树，先找到左树的最右节点mR ，绿色那个mR

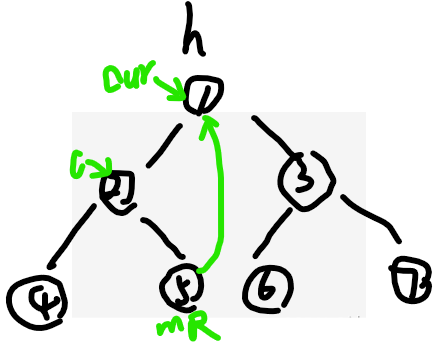
（3）如果（2）中mR.right=null，则让mR.right=cur，cur=cur.left
上图绿色的c就是cur=cur.left，去左树了，你得左边先遍历

继续回到（0）

（0）判断cur是否有左树？
（2）cur如果有左树，先找到左树的最右节点mR ，粉色那个mR

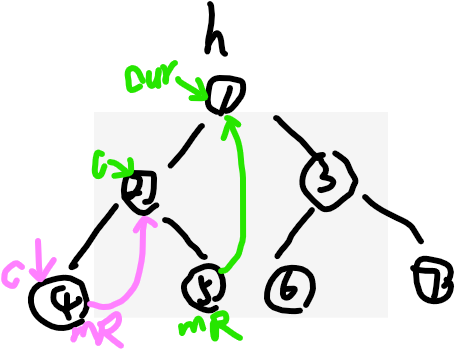
（3）如果（2）中mR.right=null，则让mR.right=cur，cur=cur.left
上图粉色的c就是cur=cur.left，去左树了，你得左边先遍历

继续回到（0）

（0）判断cur是否有左树？
（1）cur如果没有左树，直接去右树cur=cur.right（当然没有右树那停止Morris遍历），看下图蓝色c

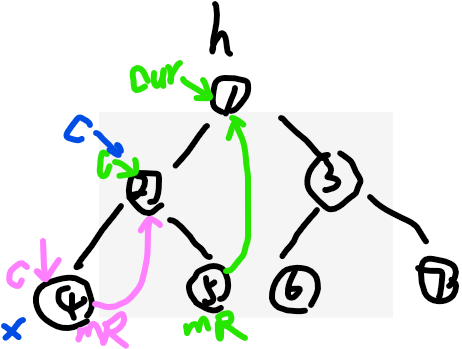
继续回到（0）

（0）判断cur是否有左树？
（4）如果（2）中mR.right=cur,则让mR.right=null，然后cur=cur.right，下面粉色那段断开，cur去橘色的c

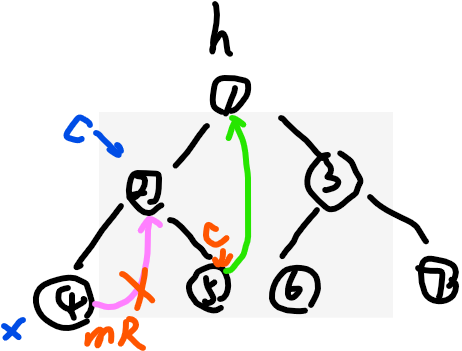
继续回到（0）

（0）判断cur是否有左树？
（1）cur如果没有左树，直接去右树cur=cur.right（当然没有右树那停止Morris遍历），看下图红色c

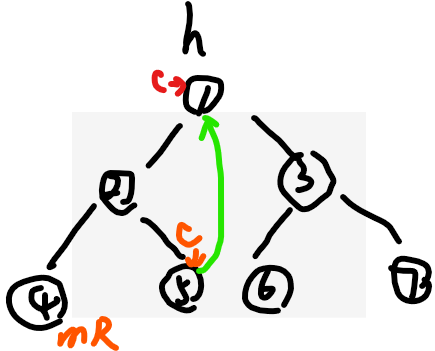
【随时熟悉Morris遍历】Morris遍历的流程：
（0）cur默认最开始指向head，mR默认为null【即cur左树的最右节点】，判断cur是否有左树？
（1）cur如果没有左树，直接去右树cur=cur.right（当然没有右树那停止Morris遍历）
（2）cur如果有左树，先找到左树的最右节点mR
（3）如果（2）中mR.right=null，则让mR.right=cur，cur=cur.left
（4）如果（2）中mR.right=cur,则让mR.right=null，然后cur=cur.right

目前cur回到了head，发现了啥？
cur有左树的话，实际上Morris会2次见到cur，比如1节点，2节点，是不是cur来了2次？
cur没有左树的话，实际上Morris只会见到cur1次，比如节点4，节点5，是不是cur来了1次？
这是Morris序的事情，一会说，咱们继续过完这个例子

继续回到（0）

（0）判断cur是否有左树？（2）cur如果有左树，先找到左树的最右节点mR
（4）如果（2）中mR.right=cur,则让mR.right=null，然后cur=cur.right，去粉色节点

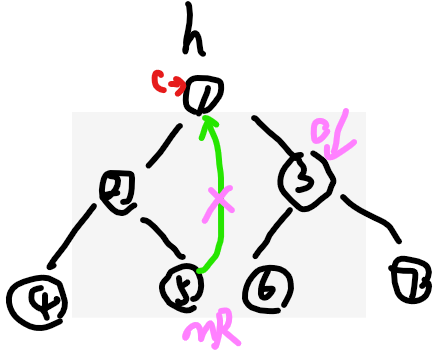
继续回到（0）

（0）判断cur是否有左树？（2）cur如果有左树，先找到左树的最右节点mR
（3）如果（2）中mR.right=null，则让mR.right=cur，cur=cur.left，去绿色c

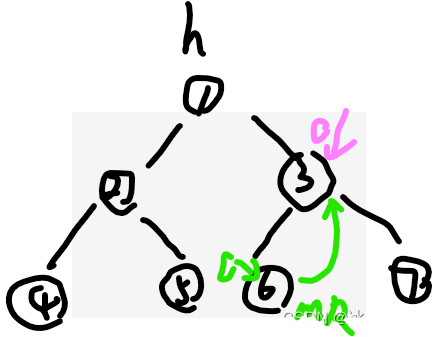
继续回到（0）

（0）判断cur是否有左树？（1）cur如果没有左树，直接去右树cur=cur.right（当然没有右树那停止Morris遍历），去蓝色c

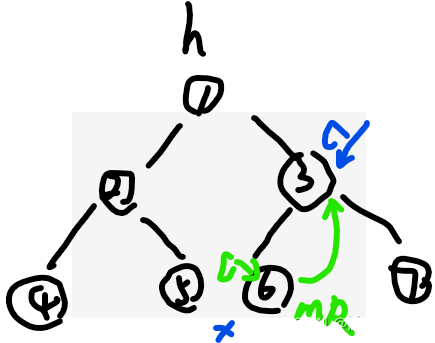
继续回到（0）

（0）判断cur是否有左树？（2）cur如果有左树，先找到左树的最右节点mR
（4）如果（2）中mR.right=cur,则让mR.right=null，然后cur=cur.right，去橘色c

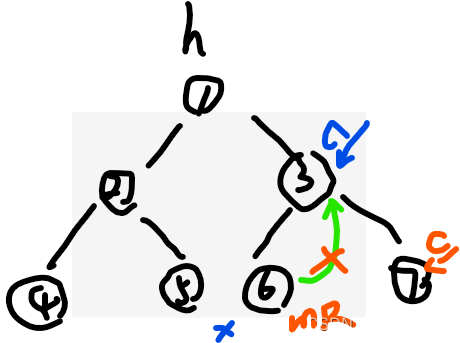
继续回到（0）

（0）判断cur是否有左树？（1）cur如果没有左树，直接去右树cur=cur.right（当然没有右树那停止Morris遍历）

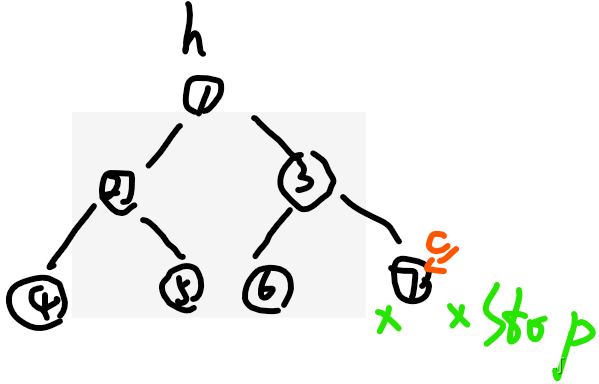
整个Morris遍历的流程走完了
是不是熟悉多了
【随时熟悉Morris遍历】Morris遍历的流程：
（0）cur默认最开始指向head，mR默认为null【即cur左树的最右节点】，判断cur是否有左树？
（1）cur如果没有左树，直接去右树cur=cur.right（当然没有右树那停止Morris遍历）
（2）cur如果有左树，先找到左树的最右节点mR
（3）如果（2）中mR.right=null，则让mR.right=cur，cur=cur.left
（4）如果（2）中mR.right=cur,则让mR.right=null，然后cur=cur.right

其实就干了这事：
来到cur就是第一次与cur见面，
当cur没有左树，找到cur左树最右节点mR，让mR指向cur，然后cur去cur左树，
mR的目的是给cur留后路，方便遍历左树之后回来cur，故有左树，见cur面2次

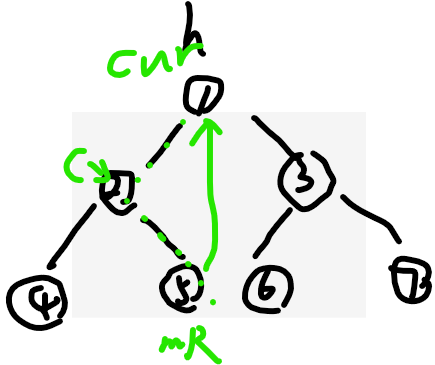
下一次见面是回到cur，然后你要把刚刚mR连上来的线断了，像这样，恢复：

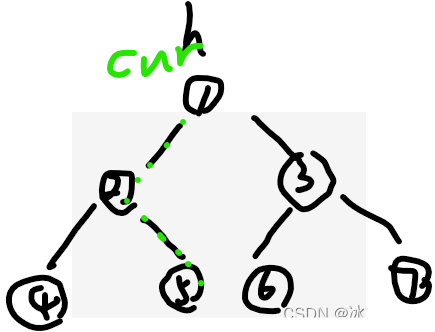
不论你cur没有左树，还是第2次见面cur，都该去遍历右树了，所有2次见面完事，cur=cur.right，因此（1）和（4）可以规划在一起写代码，精简一点，利用continue 绕过（3）

不断这么玩，相当于没有利用额外空间，用o(n）复杂度遍历了左树，右树，最后一个节点，没有右树，直接stop，Morris遍历结束！

根据上面的分析，Morris遍历，有左树的一定见面2次，没左树的只见面1次，你把cur的value打印一下，整个序列就是Morris序

---

手撕Morris遍历代码

本题所有节点，和二叉树如下：

    public static class Node{
        public int value;
        public Node left;
        public Node right;
        public Node(int v){
            value = v;
        }
    }

    //造树，长啥样呢：
    //          1
    //      2        3
    //    4   5    6   7
    public static Node createTree(){
        Node head = new Node(1);
        Node n2 = new Node(2);
        Node n3 = new Node(3);
        Node n4 = new Node(4);
        Node n5 = new Node(5);
        Node n6 = new Node(6);
        Node n7 = new Node(7);

        head.left = n2;
        head.right = n3;
        n2.left = n4;
        n2.right = n5;
        n3.left = n6;
        n3.right = n7;

        return head;
    }

【随时熟悉Morris遍历】Morris遍历的流程：
（0）cur默认最开始指向head，mR默认为null【即cur左树的最右节点】，判断cur是否有左树？
（1）cur如果没有左树，直接去右树cur=cur.right（当然没有右树那停止Morris遍历）
（2）cur如果有左树，先找到左树的最右节点mR
（3）如果（2）中mR.right=null，则让mR.right=cur，cur=cur.left
（4）如果（2）中mR.right=cur,则让mR.right=null，然后cur=cur.right

知道了这个遍历的思想，其实也不难了，手撕代码不是问题

    //复习Morris遍历
    public static void morrisReview(Node head){
        if (head == null) return;

        //【随时熟悉Morris遍历】**Morris遍历的流程：**
        //（0）cur默认最开始指向head，mR默认为null【即cur左树的最右节点】，判断cur是否有左树？
        Node cur = head;
        Node mR = null;
        while (cur != null){
            //（1）cur如果**没有左树**，直接去右树cur=cur.right（当然没有右树那停止Morris遍历）
            //没左树的，跟（4）联合精简代码
            mR = cur.left;//mR走一步先
            //（2）cur如果**有左树**，先找到**左树的最右节点mR**
            if (mR != null){
                while (mR.right != null && mR.right != cur) mR = mR.right;//往右穿
                //（3）如果（2）中mR.right=null，则让mR.right=cur，cur=cur.left
                if(mR.right == null){//打印cur，这是第1次见面
                    mR.right = cur;
                    cur = cur.left;
                    continue;//绕过（4）
                }else {//打印cur，这是第2次见面
                    mR.right = null;//mR.right=cur,则让mR.right=null，然后cur=cur.right
                }
            }
            //（1）cur如果**没有左树**，直接去右树cur=cur.right（当然没有右树那停止Morris遍历）
            //（4）如果（2）中mR.right=cur,则让mR.right=null，然后cur=cur.right
            cur = cur.right;//因为（3）那continue，不会来着，否则（1）和（4）都要来
            //这里加不加else都行，但是先序打印可能需要加else，1面就要打印
        }

    }

如果我们要打印的话
第一次见面，第二次见面咱们都打印一下

    //复习Morris遍历
    public static void morrisReviewXu(Node head){
        if (head == null) return;

        //【随时熟悉Morris遍历】**Morris遍历的流程：**
        //（0）cur默认最开始指向head，mR默认为null【即cur左树的最右节点】，判断cur是否有左树？
        Node cur = head;
        Node mR = null;
        while (cur != null){
            //（1）cur如果**没有左树**，直接去右树cur=cur.right（当然没有右树那停止Morris遍历）
            //没左树的，跟（4）联合精简代码
            mR = cur.left;//mR走一步先
            //（2）cur如果**有左树**，先找到**左树的最右节点mR**
            if (mR != null){
                while (mR.right != null && mR.right != cur) mR = mR.right;//往右穿
                //（3）如果（2）中mR.right=null，则让mR.right=cur，cur=cur.left
                if(mR.right == null){
                    //打印cur，这是第1次见面
                    System.out.print(cur.value +" ");
                    mR.right = cur;
                    cur = cur.left;
                    continue;//绕过（4）
                }else mR.right = null;//mR.right=cur,则让mR.right=null，然后cur=cur.right
            }
            //打印cur，没有左树的就打印这1次，有左树的这是第2次见面
            System.out.print(cur.value +" ");
            //（1）cur如果**没有左树**，直接去右树cur=cur.right（当然没有右树那停止Morris遍历）
            //（4）如果（2）中mR.right=cur,则让mR.right=null，然后cur=cur.right
            cur = cur.right;//因为（3）那continue，不会来着，否则（1）和（4）都要来
            //这里加不加else都行，但是先序打印可能需要加else，1面就要打印
        }

    }

测试一把：

    public static void test(){
        Node head = createTree();
        morris(head);
        System.out.println();
        morrisReviewXu(head);
    }

    public static void main(String[] args) {
        test();
    }

Morris遍历结果

1 2 4 2 5 1 3 6 3 7 
1 2 4 2 5 1 3 6 3 7 

发现没，二叉树的4567节点，没有左树，就见1次，打印1次
123有左树，就会见2次，打印2次
这就是Morris序

---

总结

提示：重要经验：

1）Morris遍历是二叉树遍历的一种，相比DFS和BFS，节省了空间，BFS还需要申请队列来搞定呢，DFS非递归那个还需要借助栈搞定呢
2）Morris遍历的流程，要熟悉，Morris序，有左树的节点见2次，打印2次，没左树的节点，见1次打印1次。
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。