解决连通性问题的利器：并查集

解决连通性问题的利器：并查集

提示：但凡设计连通性的事情，通通可以用一个利器解决：并查集
今天这篇是第一篇关于连通性的基础，今后遇到题目，我会整理出来，放一起，让你看到并查集的功能有多么强大！

---

题目

设计数据结构：并查集
（1）有很多的样本，类型为泛型V【可能是String,Integer,等等类型】
（2）最开始并查集中各个样本独立成一个集合
（3）随时可以用isSameSet 查询 ，两个元素a和b是否在同一集合中
（4）随时可以用union函数，将a和b所在的集合合并——合并集合
【（3）（4）俩大功能据定了数据集：并查集，一并一查，名字就是怎么来的】
（5）随时可以用getSetNum函数，查询整个并查集有多少个集合
（6）希望以上所有的操作都是o(1)复杂度操作！！

---

一、审题

示例：
最开始：
1 2 3 4四个整数独立为集合

查询1 2 在同一个集合中吗？
false
请问并查集中的集合有几个？
4个

然后，将1 2合并
使得1 和2变成同一个集合，其代表不妨设为1

查询1 2 在同一个集合中吗？
true
请问并查集中的集合有几个？
3个

---

并查集的实现逻辑

（1）显然，咱们给一堆数据类型为V的列表
list=（1,2,3,4）
放入并查集之后，自动生成节点和集合
节点：

//基础数据类型
    public static class Node<V>{
        public V value;
        public Node(V v){
            value = v;//初始化
        }
    }

那并查集中，我们需要一个哈希表nodesMap，映射整个list单个元素a和他的节点圈a

（2）集合咱们咋表示呢？专门找一个代表rep代表整个集合
可能1单独成立集合，1就是代表
可能1 2一起成集合，不妨设1就是代表
这样就通过一个哈希表，把所有圈a节点，它的代表，放到哈希表中parentMap里面，作为集合记录
1 2 3 4 各自做自己的代表，各自独立成一个集合的话，1挂在1自己身上，parentMap这么存
key：1节点，value：1节点

1 2 成集合的的话，1做他们集合的代表，2节点挂在1节点上，parentMap这么存
key：1节点，value：1节点
key：2节点，value：1节点（代表）

如果1 2 3 4 都是在1个集合，而1是代表的话：parentMap这么存
key：1节点，value：1节点
key：2节点，value：1节点（代表）
key：3节点，value：1节点（代表）
key：4节点，value：1节点（代表）

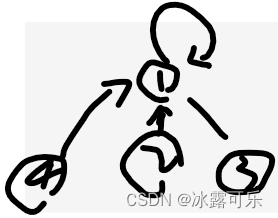
现在明白并查集中的集合怎么表示了吧？
就一个parentMap存了各个节点的代表，这个代表rep，就是一个集合表示。
任何节点x都能找到它所在的结合，只要get它x的代表即可。

（3）且问你，并查集中有几个集合呢？
显然我们只需要知道有几个代表节点，就明白了集合是几个？现在就1个代表节点，显然 1个集合。
因为现在有一个集合，所以呢，咱们需要用一个哈希表sizeMap，记录代表节点，和它代表的总节点数量
key：1，value：4【1节点下有4个节点】

如果再更加一个5节点，自己独立成绩和，那就是sizeMap：

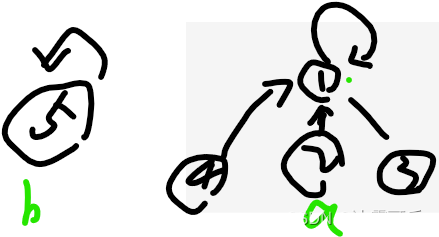
key：1，value：4
key：5，value：1【5节点下就一个节点，自己】
这样的话
咱们的集合数量就是sizeMap.size()

（4）好，如果我们要查a和b是否同同时属于同一个集合？
很简单，咱们查a和b他俩的代表，是不是同一个，是就是同一个集合？不是就false
比如，查 2 3 是同一个集合吗？？？由于他们的代表都是1，故就是同一个集合，true

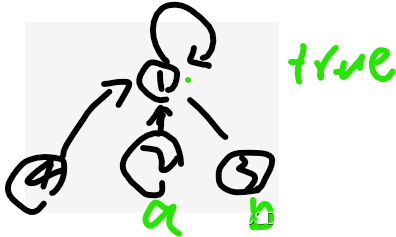
如果查2 5 是否是同一个集合，压根没有5，谈不上同一个集合
如果5独立成集合，在并查集中，那5的代表是自己，5，2的代表是1，显然两者代表不一样，故，false

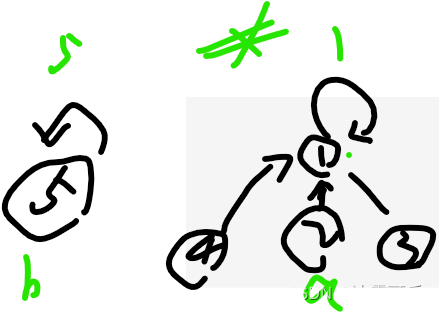
（5）现在请你，合并5所在的集合，与4所在的集合
我们看到，5的代表是5,4的代表是1，所以我们合并的时候，用小集合，挂大集合
把5挂到1上，然后在parentMap中，更新1下面的点
parentMap：
key：1节点，value：1节点
key：2节点，value：1节点（代表）
key：3节点，value：1节点（代表）
key：4节点，value：1节点（代表）
key：5节点，value：1节点（代表）

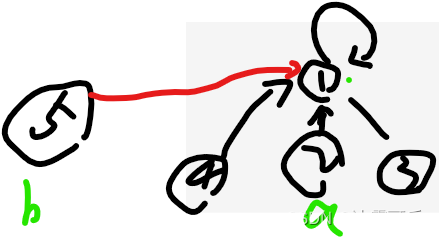
同时，更新sizeMap，因为它记录着集合代表们，和它代表集合的节点数量
sizeMap：
key：1，value：4+1=5【新增了5】
key：5，value：1 【消失】

注意，如果5集合，还有6节点呢？
先小挂大：
更新parentMap：
key：1节点，value：1节点
key：2节点，value：1节点（代表）
key：3节点，value：1节点（代表）
key：4节点，value：1节点（代表）
key：5节点，value：1节点（代表）
key：6节点，value：5节点（代表）【代表是5哦】
sizeMap：
key：1，value：4+2=6【新增了5，6】
key：5，value：2 【消失】

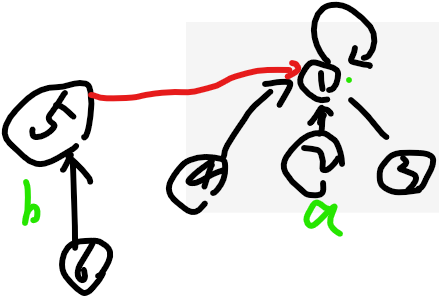
但是你注意，现在让你查6节点的代表，是不是要翻越5，然后才能去6
这个时候，就不是o(1)操作了
为了让整个并查集，都处于o(1）复杂度，咱们呢？让每一个合并俩集合时，都让所有的节点，扁平化挂到代表节点上，
这样保证，瞬间找到x的代表节点。
像这样：扁平化：

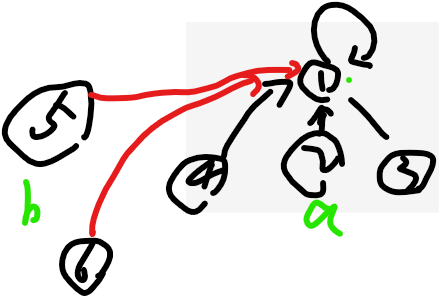
于是呢，最后parentMap：
key：1节点，value：1节点
key：2节点，value：1节点（代表）
key：3节点，value：1节点（代表）
key：4节点，value：1节点（代表）
key：5节点，value：1节点（代表）
key：6节点，value：1节点（代表）【变1了哦】

---

代码实现并查集：UnionSet

OK，整个并查集的各个函数也就实现了
总结起来就是：
（1）一次性，给你一个列表list，用里面的value们初始化并查集
建仨表，含义上面说了，一个包装节点：nodesMap，一个用来存集合代表rep：parents Map，一个存集合内部包含节点的个数：sizeMap

public HashMap<V, Node<V>> nodes= new HashMap<>();//v对应Node值为v，包装
public HashMap<Node<V>, Node<V>> parents = new HashMap<>();//节点v属于哪个节点v
 public HashMap<Node<V>, Integer> sizeMap = new HashMap<>();//我这集合的个数是多少

初始化——最开始所有元素自己独立成一个集合，包装，代表，每一个集合最开始自然就是1个节点

public UnionSet(List<V> values){
            //给的所有集合全部给它初始化
            for (V v : values) {
                Node<V> node = new Node<>(v);
                nodes.put(v, node);
                parents.put(node, node);//最开始自己属于自己
                sizeMap.put(node, 1);//一个节点
            }
        }

（2）可以随时查a和b是否在同一个集合：isSameSet
这里不得不说，查集合，就要查代表，用findFather（x）函数，返回整个集合的代表rep是谁？
那么查代表的时候，咱们完全可以给它实现（4）里面的扁平化：
比如查x=9节点的代表

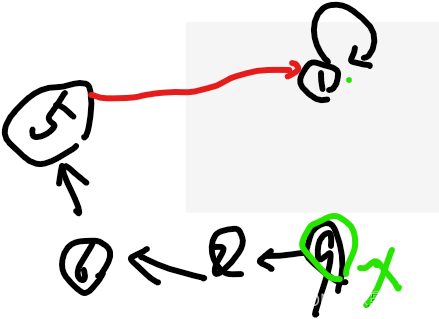
从parentMap就知道，9的代表是8,8的代表是6,6的代表是5,5的代表是1，沿途找的时候
用栈stack存下这些个所有的代表：9,8,6,5
找到了代表rep=1时，将所有这些stack中的节点9,8,6,5，全部，改挂到rep上
完成扁平化：

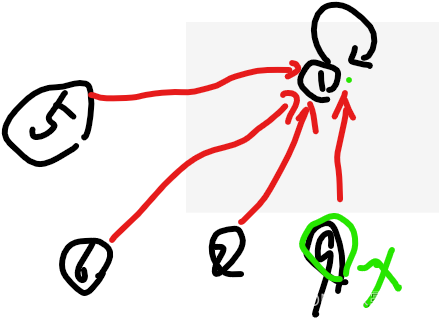
//查询俩元素他们各自的集合代表是谁，parents
        public Node<V> findFather(Node<V> cur){
            //为了保证并查集的操作复杂度为1，我们需要在查一个节点它的代表时，记下沿途的元素
            //最后让所有这些元素直接挂到代表上，很方面就找到了
            Stack<Node<V>> stack = new Stack<>();

            while (cur != parents.get(cur)){
                stack.push(cur);//记录沿途
                cur = parents.get(cur);//cur，它的代表是谁，最终代表是cur自己时那个点
            }
            //将沿途，直接挂在代表上
            while (!stack.isEmpty()) parents.put(stack.pop(), cur);//统统挂到cur

            return cur;
        }

用的时候：查a和b是否同属同一个集合，压根包装袋里面没有a或者没有b，就不可能在同一个集合

//判断俩元素是否属于同一个集合
        public boolean isSameSet(V a, V b){
            if (!nodes.containsKey(a)  || !nodes.containsKey(b)) return false;//nodes对应关系就没有ab
            return findFather(nodes.get(a)) == findFather(nodes.get(b));//俩最终找到的代表是不是同一个
        }

（3）可以查当前并查集的集合数量：getSetNum

//获取本并查集的集合个数
        public int getNum(){
            return sizeMap.size();//不是一个集合的元素个数，而是共有多少个集合
        }

（4）可以随时合并a和b所在的俩集合，小挂大，扁平化
查代表，看包装袋中没有a或者没有b的话，谈不上合并
查到了代表，代表都一样，谈不上再合并了，代表不同，咱可以合并：
把大集合代表设为big，小集合代表设为small
小挂大
大集合增加small集合，把small改挂到big就行了
大集合节点数量，增加了小集合中节点数量那么多
小集合在sizeMap中消失，代表不存在这个集合。

//将俩集合合并在一起--本质上是将小的那串，挂在大的那串上面，修改sizeMap
        public void union(V a, V b){
            //如果没有ab，不必
            if (!nodes.containsKey(a) || !nodes.containsKey(b)) return;
            //然后找他们的代表，代表相同算了，不同就要合并

            Node<V> aHead = findFather(nodes.get(a));
            Node<V> bHead = findFather(nodes.get(b));

            if (aHead != bHead){
                //把小连的头给small，大连的头给big
                int aSize = sizeMap.get(aHead);
                int bSize = sizeMap.get(bHead);

                Node<V> big = aSize >= bSize ? aHead : bHead;
                Node<V> small = big == aHead ? bHead : aHead;

                parents.put(small, big);//小挂大
                sizeMap.put(big, aSize + bSize);//更新我大的size
                sizeMap.remove(small);//把小连的个数清零
            }
        }

综合，自己手撕写一遍：
一定要自己手撕会了
闭着眼睛也能写出来

//复习实现并查集：
    public static class UnionSetReview<V>{
        //（1）一次性，给你一个列表list，用里面的value们初始化并查集
        //建仨表，含义上面说了，一个包装节点：nodesMap，一个用来存集合各个节点的代表rep：parents Map，
        // 一个存集合内部包含节点的个数：sizeMap
        HashMap<V, Node<V>> nodesMap;
        HashMap<Node<V>, Node<V>> parentMap;
        HashMap<Node<V>, Integer> sizeMap;
        //初始化——最开始所有元素自己独立成一个集合，包装，代表，每一个集合最开始自然就是1个节点
        public UnionSetReview(List<V> list){
            //一个列表，里头都是存V类型的元素，V可以是Integer啥的，随意
            //先初始化
            nodesMap = new HashMap<>();
            parentMap = new HashMap<>();
            sizeMap = new HashMap<>();

            //建独立集合，自己代表自己
            for(V k : list){
                Node cur = new Node(k);
                nodesMap.put(k, cur);//包装
                parentMap.put(cur, cur);//自己代表自己
                sizeMap.put(cur, 1);//暂时就1个
            }

        }
        //（2）可以随时查a和b是否在同一个集合：isSameSet
        //这里不得不说，查集合，就要查代表，用findFather（x）函数，返回整个集合的代表rep是谁？
        //那么查代表的时候，咱们完全可以给它实现（4）里面的扁平化：
        public Node<V> findFather(V a){
            //传入的是裸值，需要看看包装点
            Node<V> cur = nodesMap.get(a);
            if (cur== null) return null;//尽量别出现这个情况，包装传入cur是有的

            //为了实现扁平化，用栈把沿途全部加入，方便挂到代表上
            Stack<Node<V>> stack = new Stack<>();
            while (cur != parentMap.get(cur)){
                //cur的父节点不是自己，说明它不是代表
                stack.push(cur);
                cur = parentMap.get(cur);//继续往上找
            }
            //最后cur就是整个集合得代表
            while (!stack.isEmpty()){
                //沿途挂接到cur代表
                parentMap.put(stack.pop(), cur);
            }

            //返回a的代表
            return cur;
        }
        //用的时候：查a和b是否同属同一个集合，压根包装袋里面没有a或者没有b，就不可能在同一个集合
        public boolean isSameSet(V a, V b){
            //传入的是裸值，需要看包装
            if (!nodesMap.containsKey(a) || !nodesMap.containsKey(b)) return false;//没有，不可能同一个

            return findFather(a) == findFather(b);//他们的代表是同一个就代表同属一个集合
        }

        //（3）可以查当前并查集的集合数量：getSetNum
        public int getSetNum(){
            return sizeMap.size();
        }

        //（4）可以随时合并a和b所在的俩集合，小挂大，扁平化
        public void union(V a, V b){
            //裸值传入，看包装
            //查代表，看包装袋中没有a或者没有b的话，谈不上合并
            if (!nodesMap.containsKey(a) || !nodesMap.containsKey(b)) return;
            //查到了代表，代表都一样，谈不上再合并了，代表不同，咱可以合并：
            Node<V> aHead = findFather(a);
            Node<V> bHead = findFather(b);
            if (aHead != bHead){
                //把大集合代表设为big，小集合代表设为small
                int aSize = sizeMap.get(aHead);
                int bSize = sizeMap.get(bHead);
                Node<V> big = aSize >= bSize ? aHead : bHead;
                Node<V> small = big == aHead ? bHead : aHead;//否则调换头
                //**小挂大**
                //大集合增加small集合，把small改挂到big就行了
                parentMap.put(small, big);
                //大集合节点数量，增加了小集合中节点数量那么多
                sizeMap.put(big, aSize + bSize);
                //小集合在sizeMap中消失，代表不存在这个集合。
                sizeMap.remove(small);
            }
        }
    }

验证一把：

public static void test(){
        List<Integer> values = new LinkedList<>();//说明list是一个队列
        values.add(1);
        values.add(2);
        values.add(3);
        values.add(4);
        UnionSet<Integer> unionSet = new UnionSet<>(values);//放进去初始化好了，每一个节点都是一个集合
        UnionSetReview<Integer> unionSetReview = new UnionSetReview<>(values);//放进去初始化好了，每一个节点都是一个集合
        System.out.println("目前并查集有多少个集合呢？");
        System.out.println(unionSet.getNum());
        System.out.println(unionSetReview.getSetNum());

        System.out.println("查1和2是否同属同一个集合？");
        boolean iss = unionSet.isSameSet(1,2);
        boolean iss2 = unionSetReview.isSameSet(1,2);
        System.out.println(iss);
        System.out.println(iss2);

        System.out.println("将1和2所在的集合合并，再查1和2是否同属同一个集合？");
        unionSet.union(1,2);
        unionSetReview.union(1,2);
        iss = unionSet.isSameSet(1,2);
        iss2 = unionSetReview.isSameSet(1,2);
        System.out.println(iss);
        System.out.println(iss2);

        System.out.println("目前并查集有多少个集合呢？");
        System.out.println(unionSet.getNum());
        System.out.println(unionSetReview.getSetNum());
    }
   public static void main(String[] args) {
        test();
//        test2();
    }

看结果：

目前并查集有多少个集合呢？
4
4
查1和2是否同属同一个集合？
false
false
将1和2所在的集合合并，再查1和2是否同属同一个集合？
true
true
目前并查集有多少个集合呢？
3
3

---

总结

提示：重要经验：

1）并查集是解决连通性问题的最佳利器，要熟练掌握并查集的原理，实现，并一定要手撕并查集代码！
2）今后在很多题目中，可能咱们不需要包装节点，因为节点已经告诉你了，你得学会内置函数修改形参，然后运用宏观调度机制，把并查集用起来，熟悉起来。
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。