
在研究电动汽车用户充电需求的前提下,利用蒙特卡洛方法对2种不同充电方式进行模拟并对其进行分 析;分析用户响应度对电动汽车有序充电的影响,建立峰谷分时电价对电动汽车负荷影响的模型,在模拟出电动汽 车无序充电负荷的基础上,用实际案例对模型进行验证,利用多目标优化遗传算法进行求解,验证峰谷分时电价对 电网负荷优化的有效性。
部分代码:
clc
clear all
close all
t=1:24;%时间轴
N=1000;%input('请输入电动公交车数量:');
length=exp(normrnd(3.2,0.88,[1 N]));%抽取路程
pcar=zeros(1,1440);%负荷储存
start=zeros(1,N);%开始充电时间储存
T=zeros(1,N);%充电时长储存
p1=0.9699;%normspec([336,1440],1056,204,'inside');
%p2=normspec([0,336],-384,204,'inside');
%原电网24小时负荷
p0=[ 455.39
405.948
333.086
275.836
205.576
145.725
130.112
130.112
137.918
150.929
163.941
182.156
208.178
195.167
156.134
150.929
161.338
169.145
169.145
176.952
195.167
210.781
296.654
497.026];
%价格弹性矩阵,初始电价1元
priceq=[-0.623 0.3241 0.2305; %峰时弹性16-24
0.3553 -0.6166 0.2216; %平时弹性8-16
0.3215 0.3038 -0.6065]; %谷时弹性0-8
for j=1:fix(N*p1)
for i=1:5000
startt=normrnd(1056,204,[1 1]);%抽取充电初始时刻,上午五点三十六到晚上二十四点正态分布
if startt>336&&startt<=1440
start(j)=startt;
break
end
end
end
for j=(fix(N*p1)+1):N
for i=1:5000
startt=normrnd(-384,204,[1 1]);%抽取充电初始时刻,0点到5.6点
if startt>=1&&startt<=336
start(j)=startt;
break
end
end
end
for i=1:N
T(i)=length(i)*30/2.7;%充电时间
if T(i)>351
T(i)=351;
end
if (start(i)+T(i))<=1440
for m=fix(start(i)):fix(start(i)+T(i))
pcar(m)=3+pcar(m);
end
elseif (start(i)+T(i))>1440
for n=fix(start(i)):1440
pcar(n)=3+pcar(n);
end
for j=1:fix((start(i)+T(i))-1440)
pcar(j)=3+pcar(j);
end
end
end
for i=1:24
pcarrand(i)=sum(pcar((60*(i-1)+1):60*i))*0.001;
end
pcar24=pcarrand;
pcars=pcarrand;
figure
plot(t,pcars)
xlabel('时间/小时')
ylabel('充电负荷/MW')
for i=1:24
pcarrand(i)=pcarrand(i)+p0(i);
end
hold on
plot(t,pcarrand)
x(1)=0.89;%input('请输入得到的平波时电价:');
x(2)=0.79;%input('请输入得到的谷波时电价:');
x(3)=1.4;%input('请输入得到的峰波时电价:');
for i=1:24
if i>=1&&i<=8 %平时弹性分析
for j=1:8
pcar24(i)=pcar24(i)+priceq(2,2)*sum(pcar24(1:8))*(x(1)-1)/8;
end
pcar24(i)=pcar24(i)+priceq(2,2)*pcar24(i)*(x(1)-1);
for j=9:16
pcar24(j)=pcar24(j)+priceq(2,3)*sum(pcar24(9:16))*(x(1)-1)/8;
end
for j=17:24
pcar24(j)=pcar24(j)+priceq(2,1)*sum(pcar24(17:24))*(x(1)-1)/8;
end
end
if i<=16&&i>8 %谷时弹性分析
for j=1:8
pcar24(j)=pcar24(j)+priceq(3,2)*sum(pcar24(1:8))*(x(2)-1)/8;
end
for j=9:16
pcar24(i)=pcar24(i)+priceq(3,3)*sum(pcar24(9:16))*(x(2)-1)/8;
end
for j=17:24
pcar24(j)=pcar24(j)+priceq(3,1)*sum(pcar24(17:24))*(x(2)-1)/8;
end
end
if i>16&&i<=24 %峰时弹性分析
for j=1:8
pcar24(j)=pcar24(j)+priceq(1,2)*sum(pcar24(1:8))*(x(3)-1)/8;
end
for j=9:16
pcar24(j)=pcar24(j)+priceq(1,3)*sum(pcar24(9:16))*(x(3)-1)/8;
end
for j=17:24
pcar24(i)=pcar24(i)+priceq(1,1)*sum(pcar24(17:24))*(x(3)-1)/8;
end
end
end
for i=1:24
pcar24(i)=pcar24(i)+p0(i);
end
hold on
plot(t,pcar24,'-')
legend('汽车负荷曲线','优化前负荷曲线','优化后负荷曲线')
title(' 负荷优化结果')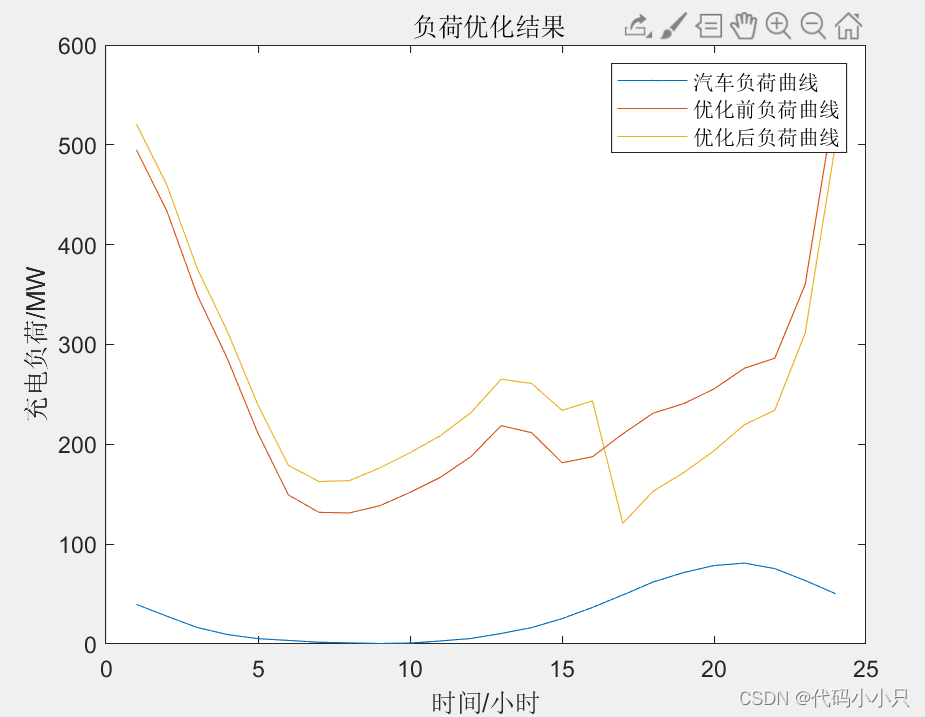







 该篇文章探讨了利用蒙特卡洛方法模拟电动汽车充电行为,分析峰谷电价对用户响应的影响,通过遗传算法优化峰谷分时电价策略,以降低电网负荷波动,提高电力系统的稳定性。
该篇文章探讨了利用蒙特卡洛方法模拟电动汽车充电行为,分析峰谷电价对用户响应的影响,通过遗传算法优化峰谷分时电价策略,以降低电网负荷波动,提高电力系统的稳定性。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








