动态规划——电路布线问题

问题描述

在一块电路板的上、下两端分别有 n 个接线柱。根据电路设计，要求用导线 (i,π(i)) 将上端接线柱 i 与下端接线柱 π(i) 相连。如下图所示，其中，π(i),1≤i≤n, 是｛1,2,…,n｝的一个排列。导线 (I,π(i)) 称为该电路板上的第 i 条连线。对于任何 1≤i≤j≤n, 第i条连线和第j条连线相交的充要条件是 π(i)>π(j).

在制作电路板时，要求将这n条连线分布到若干绝缘层上。在同一层上的连线不相交。电路布线问题要确定将哪些连线安排在第一层上，使得该层上有尽可能多的连线。换句话说，该问题要求确定导线集Nets = ｛i，π(i)，1 ≤ i ≤ n｝的最大不相交子集。

最优子结构性质

记N(i,j) = {t|(t, π(t)) ∈ Nets,t ≤ i, π(t) ≤ j }. N(i,j)的最大不相交子集为MNS（i,j）Size(i,j)=|MNS(i,j)|。

     (1)当i = 1时

   

    (2)当i >1时

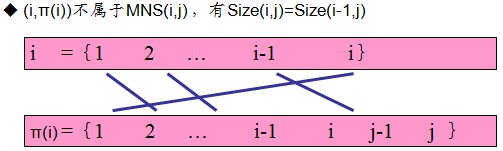
    ① j <π(i)。此时，(i,π(i)) 不属于N(i,j)。故在这种情况下，N(i,j) = N(i-1,j)，从而Size(i,j)=Size(i-1,j)。

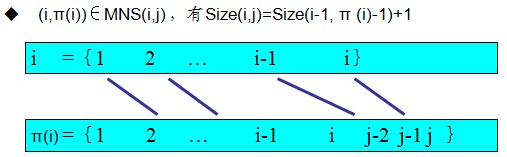
    ② j ≥π(i)。此时，若(i, π(i))∈MNS(i,j)，则对任意(t, π(t))∈MNS(i,j)有t < i且π(t)< π(i)；否则，(t, π(t))与(i, π(i))相交。在这种情况下MNS(i,j)-{(i, π(i))}是N(i-1, π(i)-1)的最大不相交子集。否则，子集MNS(i-1, π(i)-1)∪{(i, π(i))}包含于N(i,j)是比MNS(i,j)更大的N(i,j)的不相交子集。这与MNS(i,j)的定义相矛盾。

     若(i, π(i))不属于MNS(i,j)，则对任意(t, π(t))∈MNS(i,j)，有t<i。从而MNS(i,j)包含于N(i-1,j)，因此，Size(i,j)≤Size(i-1,j)。

     另一方面，MNS(i-1,j)包含于N(i,j),故又有Size(i,j) ≥Size(i-1,j)，从而Size（i,j）= Size(i-1,j)。

递推关系

     电路布线问题的最优值为Size(n,n)。由该问题的最优子结构性质可知，子问题最优值的递归关系如下：

算法：

public class Dianlubuxian {
	public int[] c;//
	public int[][] size;//最大不想交子集
	public int[] net;
	public Dianlubuxian(int[] cc){
		this.c=cc;
		this.size=new int[cc.length][cc.length];//下标从1开始
		this.net=new int[cc.length];
	}
	public void MNS(int[] c,int[][] size){
		int n = c.length-1;
		for(int j=0;j<c[1];j++){//i=1时，分了两种情况，分别等于0,1
			size[1][j]=0;
		}
		for(int j =c[1];j<=n;j++){
			size[1][j]=1;
		}
		for(int i =2;i<n;i++){//i大于1时，同样分了两种情况(当i=n时单独计算，即此方法最后一行)
			for(int j=0;j<c[i];j++){//第一种
				size[i][j]=size[i-1][j];
			}
			for(int j=c[i];j<=n;j++){//第二种
				//size[i][j]=Math.max(size[i-1][j], size[i-1][c[i]-1]+1);
				size[i][j]=size[i-1][j]>(size[i-1][c[i]-1]+1)?size[i-1][j]:(size[i-1][c[i]-1]+1);
			}
		}
		//size[n][n]=Math.max(size[n-1][n], size[n-1][c[n]-1]+1);
		size[n][n]=size[n-1][n]>(size[n-1][c[n]-1]+1)?size[n-1][n]:(size[n-1][c[n]-1]+1);
	}
	//构造最优解
	public int traceback(int[] c,int[][] size,int[] net){
		int n=c.length-1;
		int j=n;
		int m=0;
		for(int i=n;i>1;i--){
			if(size[i][j]!=size[i-1][j]){
				net[m++]=i;
				j=c[i]-1;
			}
			
		}
		if(j>=c[1])
			net[m++]=1;
		System.out.println("最大不相交连线分别为：");
		for (int t = m - 1; t >= 0; t--) {
			System.out.println(net[t]+"  "+c[net[t]]);
		}
		return m;
	}
	public static void main(String[] args) {
		int[] c = {0,8,7,4,2,5,1,9,3,10,6};//下标从1开始,第一个数，0不算,总共10个数
		Dianlubuxian di = new Dianlubuxian(c);
		di.MNS(di.c, di.size);
		int x = di.traceback(di.c, di.size, di.net);
		System.out.println("最大不相交连线数目为：:"+x);
	}
}