算法设计与分析：单源最短路径（Dijkstra），最小生成树（C/C++/Java）

C/C++：

单源最短路径：

#include <stdio.h>
 
#define M	65535 //无穷大
#define N	5 //顶点数
 
//Dijkstra算法函数，求给定顶点到其余各点的最短路径
//参数：邻接矩阵、出发点的下标、结果数组、路径前一点记录
void Dijkstra(int Cost[][N], int v0, int Distance[], int prev[])
{
    int s[N];
    int mindis,dis;
    int i, j, u;
    //初始化
    for(i=0; i<N; i++)
    {
        Distance[i] = Cost[v0][i];
        s[i] = 0;
        if(Distance[i] == M)
			prev[i] = -1;
        else
			prev[i] = v0;
    }
    Distance[v0] = 0;
    s[v0] = 1; //标记v0
    //在当前还未找到最短路径的顶点中，
    //寻找具有最短距离的顶点
    for(i=1; i < N; i++)
    {//每循环一次，求得一个最短路径
        mindis = M;
        u = v0;
        for (j=0; j < N; j++) //求离出发点最近的顶点
			if(s[j]==0 && Distance[j]<mindis)
			{
				mindis = Distance [j];
				u = j;
			} // if语句体结束，j循环结束
        s[u] = 1;
        for(j=0; j<N; j++) //修改递增路径序列（集合）
        if(s[j]==0 && Cost[u][j]<M)
        { //对还未求得最短路径的顶点
            //求出由最近的顶点 直达各顶点的距离
            dis = Distance[u] +Cost[u][j];
            // 如果新的路径更短，就替换掉原路径
 
            if(Distance[j] > dis)
            {
                Distance[j] = dis;
                prev[j] = u;
            }
        } // if 语句体结束，j循环结束
    } // i循环结束
}
// 输出最短路径
// 参数：路径前一点记录、出发点的下标、到达点下标
void PrintPrev(int prev[],int v0,int vn)
{
    int tmp = vn;
    int i, j;
    //临时存路径
    int tmpprv[N];
    //初始化数组
    for(i=0; i < N; i++)
		tmpprv[i] = 0;
 
    //记录到达点下标
    tmpprv[0] = vn+1;
    //中间点用循环记录
    for(i =0, j=1; j < N ;j++)
    {
        if(prev[tmp]!=-1 && tmp!=0)
        {
            tmpprv[i] = prev[tmp]+1;
            tmp = prev[tmp];
            i++;
        }
        else break;
    }
 
    //输出路径，数组逆向输出
    for(i=N-1; i >= 0; i--)
    {
        if(tmpprv[i] != 0)
        { //排除0元素
            printf("V%d", tmpprv[i]);
            if(i)  //不是最后一个输出符号 
                printf("-->");
        }
    }
	printf("-->V%d", vn+1);
}
//主函数
int main()
{
    //给出有向网的顶点数组
    char *Vertex[N]={"V1", "V2", "V3", "V4", "V5"};
    //给出有向网的邻接矩阵
    int Cost[N][N]={
		{0, 10, M, 30, 100},
        {M, 0, 50, M, M},
        {M, M, 0, M, 10},
        {M, M, 20, 0, 60},
        {M, M, M, M, 0},
    };
    int Distance[N]; //存放求得的最短路径长度
    int prev[N];  //存放求得的最短路径
	int i;
    //调用Dijkstra算法函数，求顶点V1到其余各点的最短路径
    //参数：邻接矩阵、顶点数、出发点的下标、 结果数组
    Dijkstra(Cost, 0, Distance, prev);
    for(i=0; i < N; i++)
    {
        //输出最短路径长度
        printf("%s-->%s:%d\t", Vertex[0], Vertex[i], Distance[i]);
        //输出最短路径
        PrintPrev(prev, 0, i);
        printf("\n");
    }
 
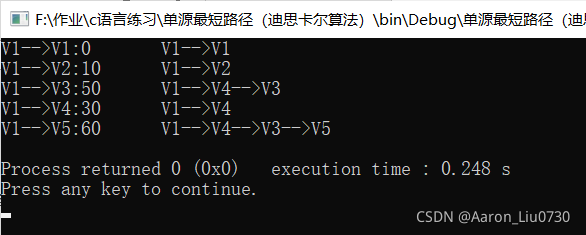
    return 0;
}

 

Java：

最小生成树：

import java.util.Scanner;

/**
 *
 * @author 刘宁宁
 */
public class MinimumSpanningTree {
    public static void main(String[] args) {
        Scanner s = new Scanner(System.in);
        System.out.println("请输入结点个数：");
        int n = s.nextInt();
        float[][] weight = new float[n+1][n+1];

        for (int i = 0; i < weight.length; i++) {
            for (int j = 0; j < weight[i].length; j++) {
                weight[i][j] = 100000;
            }
        }

        while (true) {
            System.out.println("请输入结点编号和距离（示例:1 2 3.7,输入-1退出）");
            int node1 = s.nextInt();
            if (node1 > -1){
                int node2 = s.nextInt();
                float w = s.nextFloat();
                weight[node1][node2] = w;
                weight[node2][node1] = w;
            }
            else
                break;
        }

        prim(n, weight);
    }

    public static void prim(int n, float[][] weight) {  //n为顶点数，weight为权
        float[] lowcost = new float[n + 1];  //到新集合的最小权
        int[] closest = new int[n + 1];  //与最小权对应的s集合的点
        boolean[] s = new boolean[n + 1];
        //s[i] == true代表i点在s集合中
        s[1] = true;       //将第一个点放入s集合
        for (int i = 2; i <= n; i++) {  //初始化辅助数组
            lowcost[i] = weight[1][i];
            closest[i] = 1;
            s[i] = false;
        }

        for (int i = 1; i < n; i++) {
            float min = Float.MAX_VALUE;
            int j = 1;
            for (int k = 2; k <= n; k++) {  //根据最小权加入新点
                if ((lowcost[k] < min) && (!s[k])) {
                    min = lowcost[k];
                    j = k;
                }
            }
            System.out.println(j + "," + closest[j]);  //把部分连接树输出
            s[j] = true;                    //加入新点j
            for (int k = 2; k <= n; k++) {  //根据新加入的点j,求最小权
                if ((weight[j][k] < lowcost[k]) && !s[k]) {
                    lowcost[k] = weight[j][k];
                    closest[k] = j;
                }
            }
        }
    }
}

 

单源最短路径：

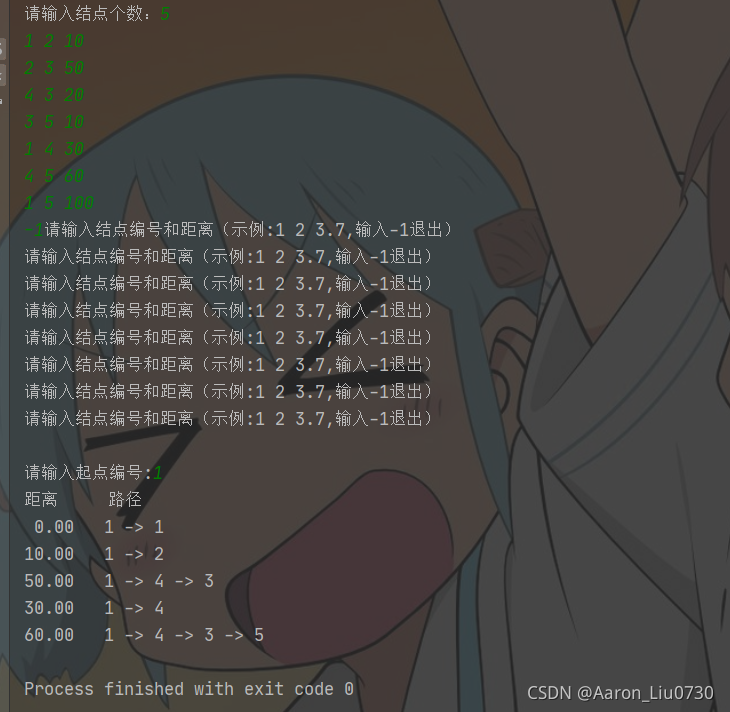
import java.util.Scanner;

public class SingleSourceShortestPath {
    public static void main(String[] args) {
        Scanner s = new Scanner(System.in);
        System.out.print("请输入结点个数：");
        int n = s.nextInt();
        int[] prev = new int[n + 1];
        float[] dist = new float[n + 1];
        float[][] a = new float[n + 1][n + 1];

        for (int i = 1; i < a.length; i++) {
            for (int j = 1; j < a[i].length; j++) {
                a[i][j] = 100000;
            }
        }

        while (true) {
            System.out.println("请输入结点编号和距离（示例:1 2 3.7,输入-1退出）");
            int node = s.nextInt();
            if (node > -1)
                a[node][s.nextInt()] = s.nextFloat();
            else
                break;
        }

        System.out.print("请输入起点编号:");
        int v = s.nextInt();
        dijkstra(v, a, dist, prev);

        System.out.println("距离     路径");
        for (int i = 1; i < dist.length; i++) {
            System.out.printf("%5.2f\t", dist[i]);
            printPath(v, prev, i);
            System.out.println(i);
        }
    }

    /**
     * @param v    起点
     * @param a    存储初始状态下的各个结点间的直接路径距离
     * @param dist 存储两个结点间的最短距离
     * @param prev 用来存放前驱结点
     */
    static void dijkstra(int v, float[][] a, float[] dist, int[] prev) {
        int n = dist.length - 1;
        if (v < 1 || v > n)
            return;       //v是起始顶点
        boolean[] s = new boolean[n + 1];  //s存储已确定最短路径的顶点

        //初始化
        for (int i = 1; i <= n; i++) {
            dist[i] = a[v][i];         // dist[i]初始化为直接连接起始点的距离
            if (dist[i] == Float.MAX_VALUE)
                prev[i] = 0;     //前驱节点为0的含义是无前驱
            else
                prev[i] = v;     //前驱节点是起始点
        }

        dist[v] = 0;
        s[v] = true;                     //起始顶点放入s

        for (int i = 1; i < n; i++) {  //循环n-1次
            float temp = Float.MAX_VALUE;
            int u = v;  //在n个结点中寻找没加入S的节点与V之间距离最小者，并加入S。
            for (int j = 1; j <= n; j++)
                if ((!s[j]) && (dist[j] < temp)) {
                    u = j;
                    temp = dist[j];
                }
            s[u] = true;
            for (int j = 1; j <= n; j++)     //新加进结点u后，重新计算没加入S的节点的距离。
                if ((!s[j]) && (a[u][j] < Float.MAX_VALUE)) {
                    float newdist = dist[u] + a[u][j];
                    if (newdist < dist[j]) {
                        dist[j] = newdist;
                        prev[j] = u;
                    }
                }
        }
    }

    static void printPath(int v, int[] prev, int i){
        if(prev[i] != v) {      //如果第i个点的前驱不是起点，则去看他前驱的前驱
            printPath(v, prev, prev[i]);
            System.out.print(prev[i] + " -> ");
        }
        else{
            System.out.print(prev[i] + " -> ");
        }
    }
}

 

qq：1351006594