C语言-螺旋数

根据下面数据排列规律，假设1点的坐标为（0，0）， x方向向右为正，y方向向下为正， 比如7的坐标为（-1，-1）， 2的坐标为（1，0），

3的坐标为（1，1）， 请编程实现输入任意点坐标（x,y）请出这点对应的数据

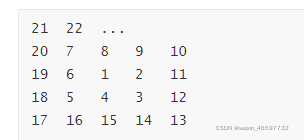
参考图像做出直角坐标系

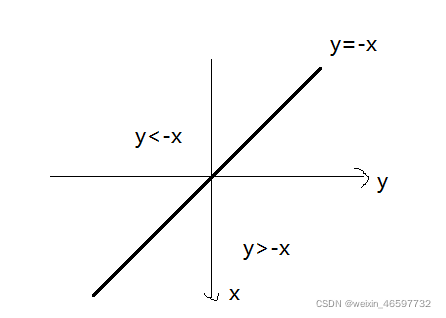
假设r为圈数，如9的圈数1,25的圈数为2，以此类推

思路一：找规律，右上对角线上的数规律为（r*2+1）的平方。

求x,y中绝对值的较大值，既该值得绝对值就是该坐标所在的圈数

即可求出该圈数的最大值，最大值的坐标为（r,-r）

并且最大值坐标距离该点坐标的距离为（r-x）+(r+y)

判断该坐标是在y=-x的左边还是右边

当坐标在左边时

该坐标的值为(r*2+1)的平方-((r-x)+(r+y)）

当坐标在右边时

该坐标的值为((r-1)*2+1)的平方+((r-x)+(r+y)）

代码：

#include<stdio.h>

int main(void)
{
    int x,y,x1,y1;
    printf("请输入x,y:");
    scanf("%d%d",&x,&y);
    x1=x>0?x:-x;
    y1=y>0?y:-y;
    int r=x1>y1?x1:y1;//求x,y中绝对值的较大值，既该值得绝对值就是该坐标所在的圈数
    int during=(r-x)+(r+y);//最大值坐标距离该点坐标的距离为（r-x）+(r+y)
    int r_sum=1;
    if(y>-x)//当坐标在右边时
    {
        r-=1;
        r_sum=(r*2+1)*(r*2+1);
        r_sum+=during;
    }else//当坐标在左边时
    {
        r_sum=(r*2+1)*(r*2+1);
        r_sum-=during;
    }
    printf("%d",r_sum);
    return 0;
}

思路二：找规律，左下对角线上的数规律为(2*r)*(2*r)+1。

        求x,y中绝对值的较大值，既该值得绝对值就是该坐标所在的圈数

        即可求出该圈数的中间值，中间值的坐标为（-r,r）

        并且中间值坐标距离该点坐标的距离为（r+x）+(r-y)

        判断该坐标是在y=-x的左边还是右边

        当坐标在左边时

        该坐标的值为(2*r)*(2*r)+1+(r+x)+(r-y)

        当坐标在右边时

        该坐标的值为(2*r)*(2*r)+1-((r+x)+(r-y))

代码：

#include <stdio.h>
#include<stdlib.h>

int main(void)
{
    int x, y;
    printf("请输入一个坐标(x,y):"); scanf("%d%d", &x, &y);

    //根据输入的x，y最大绝对值，找到左下角对角线点  abs是绝对值函数
    int r = abs(x)>abs(y)?abs(x):abs(y);

    int num = (2*r)*(2*r)+1;
  
    int res = 0;
    //判断输入的点是再右下角
    if(y>-x)
    {
        res = num-((r+x)+(r-y));
    }else
        res = num+((r+x)+(r-y));

    printf("res = %d\n", res);
    return 0;
}